Розділ 1 Структурний та кінематичний аналіз Механізма преса

1.1. Структурний аналіз механізму

Механізм преса (рис. 1) розбиваємо на механізм І класу (рис. 1а), групи ІІ класу 1 виду (рис. 1б), ІІ класу 2 виду (рис. 1в).

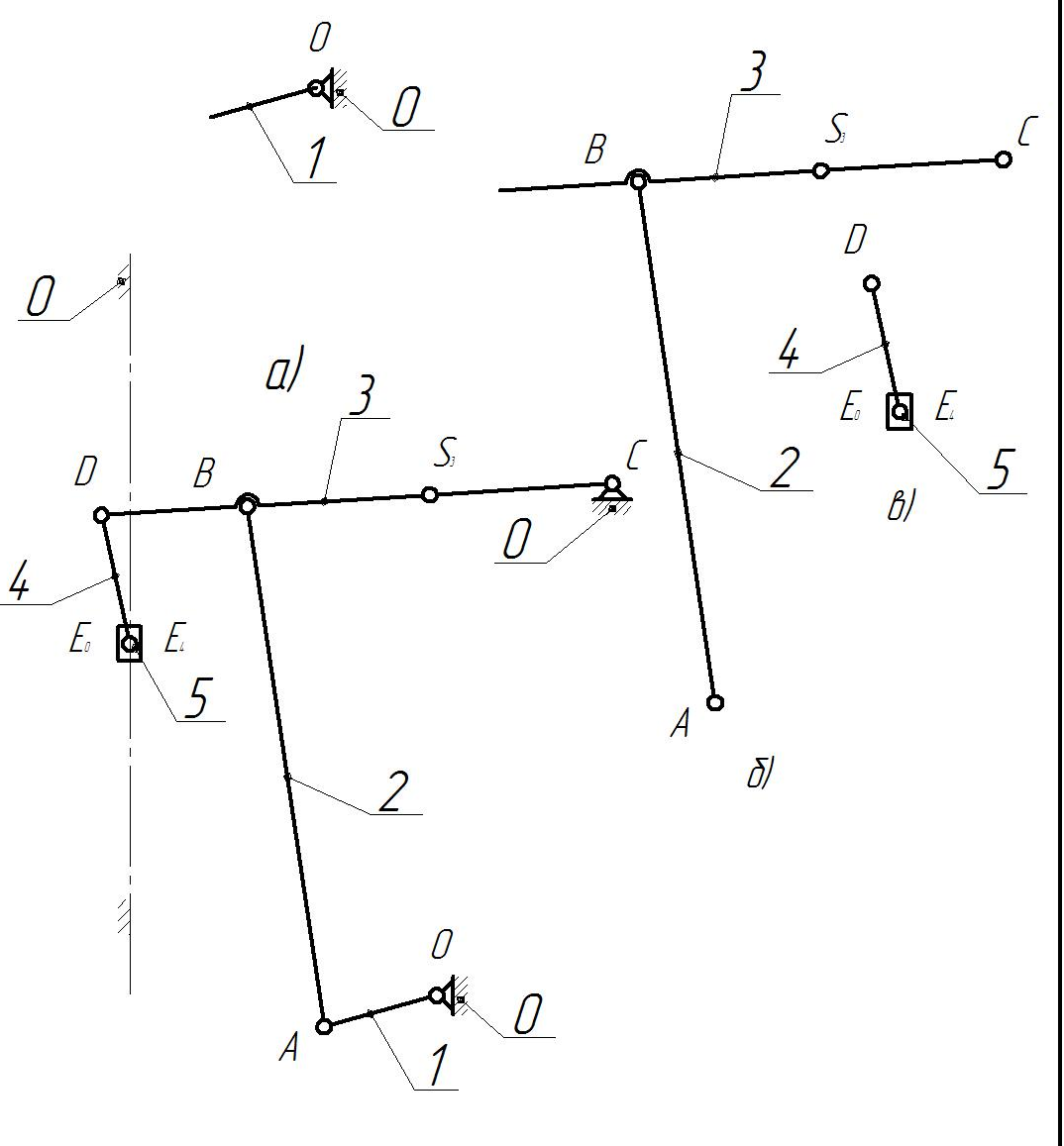
рис. 1

рис. 1 Механізм преса; а) механізм І класу; б) група ІІ класу 1 виду; в) група ІІ класу 2 виду.

Нумеруємо ланки та позначаємо кінематичні пари починаючи з механізму І класу, тоді до першої приєднаної структурної групи в напрямі від механізму І класу до стояка. Для наступної групи нумерація та позначення проводиться від вже створеного механізму знову в напрямі до стояка. механізм преса складається зі стояка 0, кривошипа 1, шатуна 2, коромисла 3, шатуна 4 та повзуна 5.

За формулою Чебишева визначаю число ступенів рухомості механізму

W = 3n – 2p₁ – p₂ = 3·5 – 2·7 – 0 = 1.

Формула будови механізму

I кл. (0, 1)  II кл. 1 в. (2, 3)  II кл. 2 в. (4, 5).

Механізм преса є механізмом ІІ класу.

1.2. Побудова плану положень механізму

План положень механізму, плани швидкостей та прискорень будуємо на лівій частині аркуша. Задаємо масштаб довжин μ_l = 0,002 м/мм. Визначаю довжину відрізків на плані:

ОА= l_OA/μ_l =0.11/0.002=55мм; АB= l_AB/μ_l =0.36/0.002=180мм;

BC= l_BC/μ_l =0.33/0.002=165мм; CD= l_CD/μ_l =0.47/0.002=235мм;

DE= l_DE/μ_l =0.12/0.002=60мм; a= l_a/μ_l =0.17/0.002=85мм;

b= l_b/μ_l =0.32/0.002=160мм; c= l_c/μ_l =0.45/0.002=225мм;

Зображуємо точки (О та С) за розмірами (a та b), та траєкторію руху точки Е, позначивши її вертикальною лінією. З точки О радіусом ОА креслимо коло яке позначає траєкторію руху кривошипа 1. Для знаходження крайніх положень точки В робимо засічки з точки О радіусом ОА+АВ=220мм та ОА-АВ=140мм на дузі, яка проведена з точки С радіусом ВС (що буде і траєкторією точки В.

…

Провівши засічку з точки С радіусом (СD) та пряму лінію через точки В і С знайшли точку D. Точка Е знаходиться на вертикальній лінії від точки D на відстані DE.

Знаходимо крайні положення механізму на яких кривошип і шатун знаходяться на одній лінії. Положення відповідають робочому ходу механізму. Траєкторію точки А ділимо на 12 рівних частин починаючи з нульового положення.

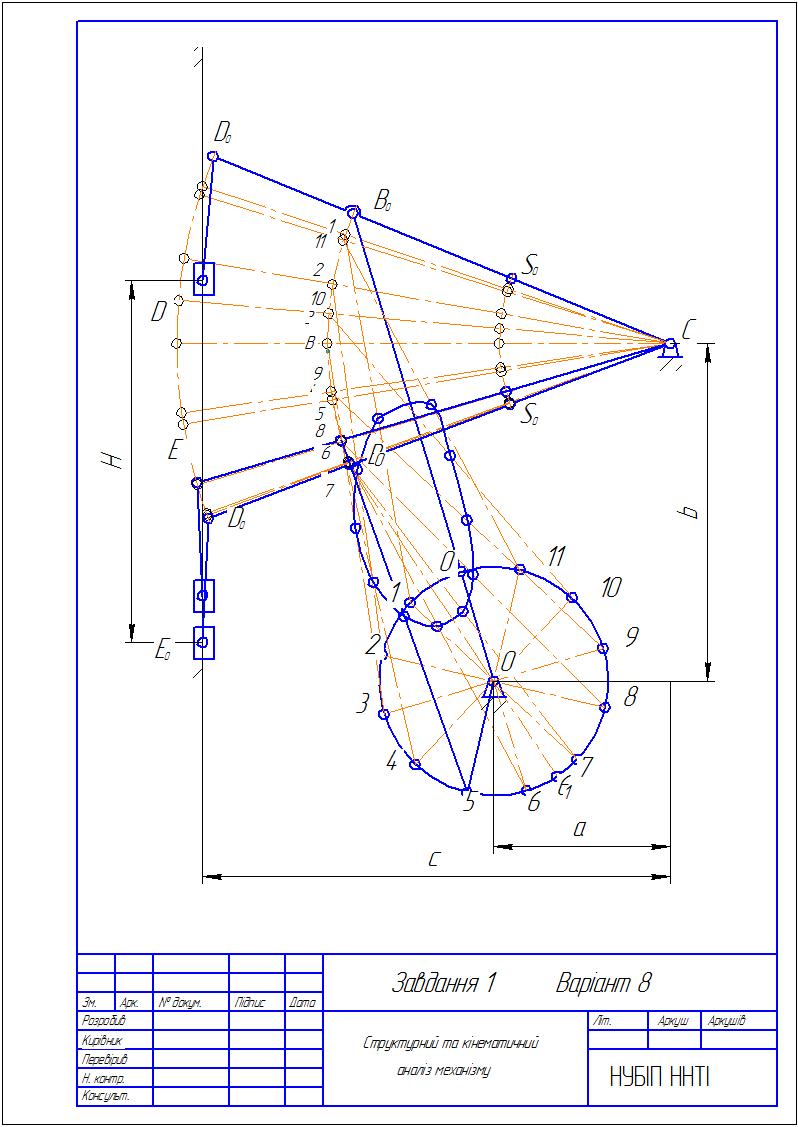
Рис. 2 план положень механізму преса.

1.3. Аналіз швидкостей методом планів

Побудуємо плани швидкостей для 13 положень механізму. методика побудови планів не залежить від номеру положення.

кутова швидкість 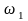кривошипа

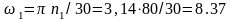с^–1

Швидкість точки а кривошипа

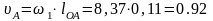м с^–1

Приймаємо масштаб швидкостей 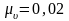мс^–1/мм. На площині вибираємо точку – полюс плану р. Швидкість точки о дорівнює нулю, тому відповідна точка о на плані співпадає з полюсом р також з полюсом співпадає і точка с, оскільки її швидкість теж дорівнює нулю.

Довжина відрізка 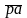, який зображує в масштабі 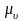швидкість точки а кривошипа, складає

мм.

Від полюса р відкладаємо перпендикулярно оа в бік обертання відрізок . швидкість точки В визначаємо у відповідності з векторним рівнянням

,

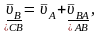
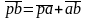де – швидкість точки В відносно А, перпендикулярна АВ. Точка В рухається навколо точки С оскільки вона знаходиться на коромислі СD, тому її швидкість та прискорення розташовуються відповідно перпендикулярно і паралельно до коромисла СD. Останнім записане векторне рівняння у відрізках плану.

З точки а проводимо перпендикуляр до АВ, а з полюса р – лінію, перпендикулярну до СD. На їх перетині знаходиться точка b.

Вимірюючи довжини відрізків рb, ab, мм, визначаємо для кожного з положень швидкості

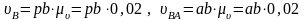, м·с^–1.

Результати цих та наступних розрахунків зводимо в таблицю 1. у ній вказуємо номер і положення механізму та кут повороту кривошипа .

знаходимо кутову швидкість шатуна 2:

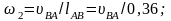с^–1.

швидкість точки D визначаємо відповідно до подібності

, с^–1.

Будуємо з полюса р відрізок рd через точку b і знаходимо розміщення точки d на плані.

Знаходимо кутову швидкість коромисла 3:

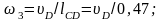с^–1.

…

….

Щоб знайти точку е на плані проводимо з полюса р паралельну лінію до стояка уу, потім з точки d проводимо перпендикуляр до шатуна DE і на їх перетині знаходимо точку е. Відповідно швидкість точки Е знаходимо згідно формули:

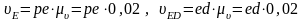, м·с^–1.

кутова швидкість коромисла 3:

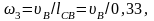с^–1.

кутова швидкість шатуна 4:

с^–1.

і	φ, град	ʋB, мс–1	ʋBA, мс–1	ω2, мс–1	ʋD, мс–1	ω3, мс–1	ʋED, мс–1	ʋE, мс–1	ω4, мс–1	ʋS2, мс–1	ʋS3, мс–1
0	0	0	0.92	2.66	0	0	0	0	0	0	0
1	30	0.63	0.44	1.22	0.89	1.89	0.28	0.84	2.33	0.76	0.31
2	60	0.90	0.56	1.6	1.28	2.72	0.22	1.22	1.83	0.91	0.45
3	90	0.92	0.27	0.75	1.31	2.79	0.08	1.33	0.66	0.91	0.46
4	120	0.77	0.56	1.55	1.09	2.32	0.18	1.11	1.5	0.80	0.26
5	150	0.50	0.80	0.29	0.71	1.51	0.20	0.69	1.66	0.62	0.25
6	180	0.19	0.93	2.58	0.27	0.57	0.09	0.25	0.75	0.45	0.09
7	210	0.15	0.86	2.40	0.21	0.44	0.07	0.21	0.58	0.49	0.08
8	240	0.55	0.52	1.44	0.78	1.66	0.23	0.76	1.92	0.71	0.28
9	270	1.02	0.18	0.5	1.45	3.09	0.21	1.47	1.75	0.97	0.51
10	300	1.31	1.03	2.86	1.87	3.98	0.17	1.83	1.42	1.01	0.65
11	330	0.87	1.31	3.65	1.24	2.64	0.37	1.17	3.08	0.61	0.44

За теоремою подібності знаходимо швидкості центрів мас шатунів. На прямій аb відкладаємо відрізок

,

а на прямій ac відрізок

.

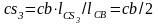Швидкості: , м·с^–1