Завдання.
Визначити загальне проективне покриття за допомогою сітки Л.Г. Раменського.
Визначити зімкнутість крон за допомогою зеркальної сітки.
Обрахувати відсоток покриття окремих видів у фітоценозі методом масштабної проекційної сіточки.
Визначити проективне покриття крапчатим методом.
Зробити висновки.
20
Лабораторна робота № 4
Тема: Застосування статистичних методів для
дослідження фітоценозів.
Мета: за допомогою статистичних методів визначити показники, що вказують на найбільш типовий рівень розвитку угруповання.
Обладнання: статистичні дані рослинних угруповань (таблиці), калькулятор.
Застосування статистичних методів в біології набуло таких особливостей, що можна вважати біологічну статистику невід'ємною частиною досліджень угруповань організмів.
В даній роботі використовуються статистичні методики П. Ф. Рокітцкого.
Рослинні організми характеризуються мінливістю та варіацією за різними ознаками. При вивченні біологічних угруповань, виявилось доцільним застосовувати статистичних дані.
Число одиниць сукупності називають об'ємом сукупності (n),
а варіацією – зміну значень ознаки. Варіанта (хі) - одне із значень, де і - означає порядковий номер варіанту.
Після підрахунку та розподілу всіх варіантів за класами утворюються ряди, в яких показано, як часто зустрічається певна варіанта. Класи з найбільшою частотою називаються модальні, а з найменшою – граничні.
Після підрахунку середнього арифметичного:
Необхідно вирахувати стандартне відхилення (варіанту):
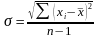
21
та коефіцієнт варіації:
Вищезгадані характеристики дають можливість вичерпно охарактеризувати біологічні сукупності, які можуть бути представлені у вигляді ряду розповсюдження. Для цього ряду можна визначити статистичні показники, що вказують на найбільш типовий рівень розвитку угруповання, яке визначається, в сукупності ознаки і на всю ступінь варіації окремих одиниць сукупності навколо цього рівня. Але так як всі ці величини - це статистичні дані, то виникає питання наскільки вони достовірні.
Загальні закономірності випадкової варіації дають можливість підійти до питання про оцінку достовірності статистичних показників. Генеральна (х) та вибіркова (µ) сукупності характеризуються однаковими закономірностями випадкової варіації. Певні значення середніх арифметичних вибірок варіюють навколо середнього арифметичного генеральної сукупності. Варіація ж вибіркових середніх навколо μ може бути змінена своїм середнім квадратичним відхиленням, своєю σ. Ця сигма отримала назву середньої похибки, або середньої квадратичної помилки.
Інколи її ще називають стандартною похибкою (m) - вона вказує на ступінь зближення значень х та μ і вираховується за формулою:
З наведеної вище формули очевидно, що розмір визначеної середньої похибки залежить від σ і вибіркової популяції та її об'єму. Чим краще взята вибірка і чим більше її розмір, тим менша середня похибка. У зв'язку між статистичними показниками вибіркової та генеральної сукупностей віддзеркалюється, так званий, закон великих чисел – чим більше число n, деяких впадкових величин, тим їх середнє арифметичне ближче до середнього арифметичного генеральної сукупності, тим менше різниця між х та μ (Чебишев); при збільшенні n (n=∞), то х та μ прямують до 1, тобто до повної вірогідності. Для встановлення вірогідності різниці між середніми арифметичними використовують нормативне відхилення (t):
22
Де х1 – х2 – середнє арифметичне, S(х1– х2) – середнє відхилення. Якщо х1– х2= d, то
Якщо різниця перевищує свою похибку у 3 рази, то її вірогідність не менше 0,99, при n> 30, t = 2,58 (за таблицями).
При порівнянні двох груп з малими n помилка різниці вираховується за формулою:
якщо t ≥ 3, то різницю між сигмами можна вважати достовірно - ''суттєвою".
Завдання:
За допомого статистичних даних рослинних угруповань (таблиці) визначити:
середнє арифметичне значення одієї із ознак рослини (x);
стандартне відхилення (варіанту) (σ);
коефіцієнт варіації (V);
стандартною похибкою (m);
нормативне відхилення (t);
помилку різниці (Sd).
Встановити найбільш типовий рівень розвитку угруповання.
Зробити висновки.
23