2. Булеан множества

Каждое множество порождает новое множество несколько необычным образом.

ОПРЕДЕЛЕНИЕ 1. Булеаном множества A называется совокупность всех подмножеств множества A. Обозначение:

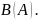
Примеры. 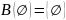(единственный элемент булеана – пустое множество). (у одноэлементного множества два подмножества: пустое и само множество).

Упражнение. Запишите булеаны множеств {a,b}, {a,b,c}. Подсчитайте число элементов каждого из булеанов.

Из предыдущего упражнения следует гипотеза, подтверждение которой это следующий факт.

Теорема 1. 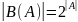для конечного множества A. Здесь и далее |A| - число элементов конечного множества. Для множеств бесконечных смысл этому символу будет придан ниже.

Доказательство. Пусть A={a₁,a₂,…,a_n}. Каждому подмножеству A можно сопоставить вектор длины n, элементами которого являются числа 0 и 1, где единицы соответствуют тем элементам, которые входят в подмножество. Например, подмножеству {a₁,a₃}{a₁,a₂,a₃,a₄} соответствует вектор (1,0,1,0). Справедливо и обратное: каждому вектору длины n из 0 и 1 соответствует подмножество A. Таким образом, число элементов булеана равно числу таких векторов. Но это просто число размещений с повторениями из 2 по n, т.е. 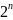(см. п. 1.2), что и требовалось.

3. Прямое произведение множеств

ОПРЕДЕЛЕНИЕ 2. Прямым произведением множеств A₁, A₂,…, A_n называется множество

A₁A₂… A_n={(a₁ a₂,…,a_n): a₁A₁, a₂A₂,…, a_nA_n}.

Элементы прямого произведения (a₁ a₂,…,a_n) называются векторами или кортежами. Слово «кортеж» вам встречалось, возможно, в обороте «кортеж автомобилей». Так говорят, когда едет группа крупных руководителей. Следуют они в определенном порядке: первым едет самый большой начальник, вторым начальник поменьше, и т.д. Здесь тоже элементы стоят на определенных местах, правда, первый элемент не важнее второго.

Прямое произведение считается пустым, если один из сомножителей – пустое множество.

Упражнение. Перечислите все элементы прямого произведения {1,2} {a,b}.

Если множества совпадают, то пишут просто Aⁿ.

Поначалу может показаться, что приведенная конструкция несколько искусственная. В действительности, вы часто сталкиваетесь с ней, не говоря уже о том, что именно на прямом произведении множеств базируется реляционная модель базы данных – один из важнейших элементов программного обеспечения.

Примеры.

1. В зрительном зале 30 рядов, в каждом по 26 мест. Прямое произведение {1,2,…,30}{1,2,…,26} это представление множества всех зрительских мест.

2. Прямое произведение {a,b,…,h}{1,2,…,8} это множество полей шахматной доски.

3. Пусть R – множество вещественных чисел. Тогда R² это множество точек плоскости, заданных обычными декартовыми координатами (х,y). Аналогично R³ – множество точек пространства. Можно пойти дальше и рассмотреть n-мерное пространство Rⁿ. Многомерные пространства используются в физике (есть теории, в соответствии с которыми наше реальное пространство 10- или 16-мерное), используются они и в экономике.

Словом, прямые произведения вам встречались и раньше, но подобно герою Мольера, который с удивлением узнал, что разговаривает прозой, вы не знали, что это так называется.

Подчеркнем отличия между множеством (там используются фигурные скобки) и прямым произведением.

{a,b}={b,a}, (a,b)(b,a), {a,b,a}={a,b}, вектора (a,b,a) и (a,b) расположены в разных пространствах, сравнение их лишено смысла.

Приведем еще одну конструкцию, связанную с прямым произведением. Определим алфавит A – конечное множество {a₁,a₂,…,a_n}, элементы которого называются буквами. Языком над алфавитом A называются всевозможные последовательности букв. Таким образом, язык это множество AA²A³…Aⁿ… . Разумеется, среди этих «текстов» большинство бессмысленных (например, целые тома, заполненные одной буквой).

Следующее утверждение очевидно.

Теорема 2. Если A₁, A₂,…, A_n – конечные множества, то |A₁A₂… A_n|=|A₁||A₂|…| A_n|.