4. Перестановки

1. .Сколькими способами могут встать в очередь 10 человек?

2. . Каков ответ в задаче 1.3.3, если студентов 20?

3. . Каков ответ в задаче 1.3.4, если различных стульев 10?

4. . Сколько существует размещений без повторений из n по n?

Ответ: n! Такие размещения называются перестановками. Перечислите все перестановки из 3 элементов. Иногда число перестановок из n обозначают P_n.

5. Сочетания (без повторений)

1. .В шахматном турнире участвовали 10 человек. Сколько состоялось партий, если каждая пара игроков встретилась один раз?

2. .Из колоды карт (36 штук) игрок получает 6. Сколько различных наборов он может получить?

3. .Каков ответ в задаче 1.2.2, если все призы одинаковые?

4. .Каков ответ в задаче 1.2.4, если все стулья одинаковые?

5. .(Обобщение) Сколько в n-элементном множестве существует m-элементных подмножеств? Ответ:

.

В комбинаторике такие подмножества принято называть сочетаниями (без повторений) из n по m. Число сочетаний обозначается 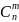(старое обозначение) или (современное обозначение). Еще эти величины называются биномиальными коэффициентами (смысл этого названия прояснится далее). Перечислите все сочетания из 3 по 2.

6. . Город имеет форму прямоугольника, улицы идут строго с юга на север или с запада на восток. Улиц первого направления (n+1), второго – (m+1). Сколькими различными путями можно пройти из юго-восточного угла города в северо-западный так, чтобы путь был кратчайшим?

7. . Докажите, что

.

Эта формула называется биномом Ньютона. На самом деле она была известна еще арабским средневековым математикам, Ньютону принадлежит заслуга ее обобщения на случай произвольных показателей.

6. Свойства биномиальных коэффициентов

1. Докажите, что . Сделайте это четырьмя способами: по определению, по формуле и используя результаты задач 1.5.6 и 1.5.7.

2. Докажите, что

.

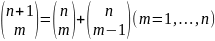Сделайте это также четырьмя способами.

3. (Треугольник Паскаля). Найдите число, которое расположено на m-ом месте n-й строки таблицы чисел

Здесь каждое число равно сумме двух чисел, расположенных над ним (вне таблицы расположены нули).

4. Вычислите .

7. Разбиения множеств

Число сочетаний можно интерпретировать как число способов, которым n-элементное множество можно разбить на два подмножества, в одном из которых m, а во втором ( ) элементов. Этот подход допускает существенное обобщение.

1. В группе 25 студентов. 12 из них надо отправить на практику на одно предприятие, 8 на второе, 5 на третье. Сколькими способами это можно сделать?

2. Сколькими способами можно расположить в цепочку (переставить) 12 предметов трех типов, если предметов каждого типа по 4? Предметы каждого типа одинаковые.

3. (Обобщение) Множество из n различных предметов раскладывают в m различных ящиков. В первый помещают r₁, во второй r₂,…, в m-й – r_m предметов (r₁+ r₂+…+r_m=n). Сколькими способами это можно сделать?

Ответ: . Эти величины обозначаются (при m>2) и называются полиномиальными коэффициентами, поскольку равны коэффициентам при произведениях вида

в разложении .