3.2 Построение модели стоимости жилой недвижимости в городах Ярославской области

Составленную нами выборку [Приложение 2] необходимо проверить на соответствие нормальному закону распределения.

Для этого мы предварительно рассчитали основные статистические характеристики.

Основными из полученных характеристик, необходимых для дальнейшей работы с выборкой является среднее и стандартное (среднеквадратическое )отклонение = 9757,576779.

Таблица 8

Основные статистические характеристики

Среднее	38793,725
Стандартная ошибка	1090,930249
Медиана	35000
Мода	33333
Стандартное отклонение	9757,576779
Дисперсия выборки	95210304,61
Эксцесс	-0,358798748
Асимметричность	0,989125588
Интервал	35000
Минимум	25000
Максимум	60000
Сумма	3103498
Счет	80

Воспользуемся приближенными методами проверки нормальности распределения – это проверка по коэффициенту вариации, по критерию среднего абсолютного отклонения и по размаху варьирования.

Проверка по коэффициенту вариации

Рассчитаем значение коэффициента вариации, используя уже рассчитанные ранее значения выборочного среднего и среднеквадратичного отклонения, по формуле (2.17) и получаем:

Полученное значение коэффициента вариации меньше 33%, следовательно, согласно данному критерию распределение может считаться нормальным и проверку можно продолжить далее.

Проверка с помощью критерия среднего абсолютного отклонения

Среднее абсолютное отклонение определим по формуле (2.16):

Проверим, выполняется ли соотношение:

После вычисления получаем верное неравенство 0,0069 < 0,0447 . Следовательно, согласно данному критерию, выборка удовлетворят требованиям нормального распределения.

Для того, что бы привести составленную нами статистическую совокупность к виду, пригодному для дальнейших расчетов, необходимо качественные ценообразующие факторы перевести в количественные. Для этого наилучшему значению признака мы присвоили значение порядковой шлалы «5», наихудшему значение признака нами было присвоено порядковое значение «1».

Полученные данные необходимо исследовать на наличие выбросов и мультиколлинеарности.

Исследование данных на наличие выбросов проверяем с помощью критерия Смирнова-Граббса, так как объем выборки превышает 25.

Определим уровень критерия Смирнова-Граббса при объеме выборки равной 80 и уровне значимости α=0,05, S_крит=3,28.

Для нахождения S_расч используем формулу 2.11.

Получив расчетные значения S, сравним их с критическим, все S_расч экспериментальной выборки меньше S_крит. Это значит, что выбросов среди данной выборки нет.

Далее проведем проверку на зависимость между выбранными нами ценообразующими факторами и результирующим показателем. Воспользуемся инструментальными средствами MS Exel для нахождения корреляционной матрицы [Приложение3]. Анализируя полученные данные, можно сказать, что на стоимость одного квадратного метра наименьше влияние оказывает материал стен дома (r_ху2 = -0,032), наибольшее влияние на результирующий показатель оказывает престижность района (r_ху11= 0,702).

Существует тесная связь между инфраструктурой района и престижностью района (r_х11x13 = 0,935) и между инфраструктурой района и уровнем строительства в городе (r_х13x14 = 0,937). Следовательно, в дальнейшем для построения регрессионной модели из выборки мы исключаем фактор – инфраструктура района.

После исследование данных на наличие выбросов и мультиколлинеарности можно приступить к построению модели.

Уравнение будет иметь вид:

(3.1)

Найдем значения параметров множественной регрессии.

Коэффициент детерминации является одной из обобщенных мер качества модели оценки. Он показывает, какую долю изменения рыночных цен объясняют факторы, включенные в модель оценки, и рассчитывается по формуле 2.18:

Таблица 9

Коэффициенты регрессии и статистика переменных

	Коэффиц иенты	Станд ошибка	t-стат	P- Знач	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
Y-пересе чение	19760,96	3245,65	6,089	0,000	13280,81	26241,12	13280,81	26241,12
Тип дома	272,91	590,67	0,46	0,645	-906,39	1452,22	-906,39	1452,227
Материал стен	-371,45	425,24	-0,87	0,385	-1220,47	477,56	-1220,47	477,5646
Этаж	293,12	202,21	5	0,152	-110,58	696,82	-110,58	696,8287
Этаж-ть	-557,76	210,04	-2,65	0,009	-977,13	-138,39	-977,13	-138,397
Общая площадь	-552,19	166,63	-3,31	0,001	-884,88	-219,49	-884,88	-219,497
Жилая площадь	73,06	238,98	0,31	0,760	-404,08	550,21	-404,08	550,2178
Площадь кухни	836,93	365,54	2,29	0,025	107,11	1566,75	107,11	1566,758
Тип санузла	-197,03	438,30	-0,45	0,654	-1072,13	678,06	-1072,14	678,0693
Лоджия/ балкон	275,20	427,98	0,64	0,522	-579,29	1129,69	-579,29	1129,699
Состояние	1225,25	282,44	4,32	0,000	661,34	1789,17	661,34	1789,173
Район	10238,54	736,40	13,90	0,000	8768,27	11708,82	8768,27	11708,82
Удален ность	5363,17	357,24	15,01	0,000	4649,90	6076,44	4649,90	6076,441
Застраи ваемость	-4917,34	605,59	-8,12	0,000	-6126,44	-3708,24	-6126,45	-3708,24

Коэффициент детерминации всегда лежит в интервале от 0 до 1. Чем ближе значение коэффициента детерминации к единице, тем лучше модель описывает исходный ряд данных.

Скорректированный коэффициент детерминации (2.19):

Это означает, что регрессионная модель оценки стоимости на 89% объясняет изменение стоимости в экспериментальной выборке. Остальные 11% вариации стоимостей выборки обусловлены факторами, не учитываемыми моделью.

В общем случае, для того чтобы модель считалась статистически надежной, например, с не менее чем 95% вероятностью, необходимо, чтобы выполнялось неравенство: Значимость F ≤ 0,05.

Таблица 10

Регрессионная статистика

Множественный R	0,953024
R-квадрат	0,908255
Нормированный R-квадрат	0,890184
Стандартная ошибка	3233,501
Наблюдения	80

Таблица11

Дисперсионный анализ

	df	SS	MS	F	Значимость F
Регрессия	13	6831474372	525498029	50,26	0,000000000000000000000000000045
Остаток	66	690064929	10455529
Итого	79	7521539302

Коэффициент детерминации всегда лежит в интервале от 0 до 1. Чем ближе значение коэффициента детерминации к единице, тем лучше модель описывает исходный ряд данных.

Скорректированный коэффициент детерминации (2.19):

Это означает, что регрессионная модель оценки стоимости на 89% объясняет изменение стоимости в экспериментальной выборке. Остальные 11% вариации стоимостей выборки обусловлены факторами, не учитываемыми моделью.

В общем случае, для того чтобы модель считалась статистически надежной, например, с не менее чем 95% вероятностью, необходимо, чтобы выполнялось неравенство: Значимость F ≤ 0,05. Если принять статистическую значимость на уровне 90%, то нужно добиваться выполнения неравенства Значимость F ≤ 0,01.

В данной модели Значимость говорит о возможности принятия значимости на уровне выше 95%, так как в нашей модели уровень значимости F-критерия составляет 0,000000000000000000000000000045.

Так как некоторые Р-значения факторов уравнения превышают 0,05. Если это значение меньше 0,05, то соответствующий коэффициент является значимым. Если же p-значение для какого-либо коэффициента больше 0,05, то он является статистически незначимым.

Поэтому можно сделать вывод о не значимости двух факторов: тип дома, материал стен, эта, жилая площадь, тип санузла, наличие балкона(лоджии).

На второй итерации спецификация модели будет иметь вид:

(3.2)

Найдем значения параметров множественной регрессии.

Удалив их из модели, получим следующие коэффициенты регрессии и статистику переменных, показанные в таблице 12.

Коэффициент детерминации является одной из обобщенных мер качества модели оценки. Он показывает, какую долю изменения рыночных цен объясняют факторы, включенные в модель оценки, и рассчитывается по формуле (2.18):

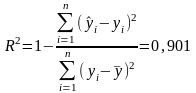
Таблица 12

Коэффициенты регрессии и статистика переменных

	Коэффиц иенты	Стандарт ошибка	t-стат	P-Знач.	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
Y-пересе чение	20443,07	2641,35	7,74	0,000	15177,6	25708,5	15177,6	25708,5
Этажность	-341,06	171,16	-1,99	0,051	-682,25	0,14	-682,25	0,14
Общая площадь	-547,46	115,58	-4,74	0,000	-777,86	-317,05	-777,86	-317,05
Площадь кухни	917,33	343,44	2,67	0,009	232,70	1601,97	232,70	1601,97
Состояние	1348,78	266,18	5,07	0,000	818,17	1879,39	818,17	1879,39
Престижн ть	9841,28	686,13	14,34	0,000	8473,50	11209,06	8473,50	11209,06
Удален-ть	5292,47	343,41	15,41	0,000	4607,90	5977,03	4607,90	5977,03
Застраива емость	-4656,48	577,57	-8,06	0,000	-5807,84	-3505,12	-5807,84	-3505,12

Коэффициент детерминации является одной из обобщенных мер качества модели оценки. Он показывает, какую долю изменения рыночных цен объясняют факторы, включенные в модель оценки, и рассчитывается по формуле (2.18):

Скорректированный коэффициент детерминации (2.19):

Это говорит о том, что были удалены не значимые переменные и значимость и прогнозные качества модели изменены не были.

Для второй итерации уровень значимости F-критерия составляет 0,00000000000000000000000000000000125. Так как данное значение существенно меньше 0,01, то полученная модель является высоко значимой.

Таблица 13

Регрессионная статистика

Множественный R	0,949398884
R-квадрат	0,90135824
Нормированный R-квадрат	0,891768069
Стандартная ошибка	3210,092314
Наблюдения	80

Таблица 14

Дисперсионный анализ

	df	SS	MS	F	Значимость F
Регрессия	7	6779601430	968514490	93,99	0,00000000000000000000000000000000125
Остаток	72	741937872	10304692,7
Итого	79	7521539302

Р-значения для всех коэффициентов меньше 0,05. Это говорит о том, что в данной выборке все значимые коэффициенты, то есть факторы, соответствующие этим коэффициентам должны быть включены в модель.

Получим следующую модель подставив β-коэффициенты из таблицы 12 в формулу (3.2):

Проведем проверку полученной модели. Определим цену предложения однокомнатной квартиры, расположенной в городе Ярославле по адресу улица Урицкого д. 63 на 5 этаже, тип дома (тип планировки) – хрущевка, материал стен – кирпич, общая площадь квартиры 33 м² с лоджией. При подаче объявления продавец охарактеризовал состояние квартиры как хорошее и предложил купить её за 2 120 000 рублей, стоимость одного квадратного метра составляет 64 242 рубля. Для расчета по модели полученной регрессионным методом необходимо определить ценообразующие факторы так, как это было сделано для выборки, используемой при расчетах. Уравнение модели для расчета цены предложения квартиры будет иметь вид:

Цена предложения данной квартиры на рынке составляет 64 242 рубля за м². Расчетное значение стоимости отличается от рыночного на 180 рублей. Следовательно, построенную нами регрессионную модель без сомнений можно использовать на вторичном рынке жилой недвижимости в городах Ярославской области.

Заключение

Оценка рыночной стоимости объектов недвижимости для любых целей как процесс состоит из изучения самого объекта оценки и рынка объекта оценки, создания экономико-математической модели этого рынка и собственно оценки объектов недвижимости, входящих в этот рынок.

Одной из основных задач государства в рыночной экономике является формирование и исполнение объективно сбалансированного бюджета в интересах удовлетворения социально-экономических потребностей граждан государства. В условиях рынка эта задача должна решаться на основе рыночных законов ценообразования.

Недвижимость является одним из надежнейших источников доходной части бюджета в виде налоговых и арендных платежей. Базой для налоговых и арендных платежей должна являться рыночная стоимость объектов недвижимости, которая зависит от целого ряда ценообразующих факторов: местоположение, состояние, окружение, экология и многое другое. Государство через систему нормативно-правовых актов может влиять на рыночную стоимость посредством создания такого набора ценообразующих факторов, который будет увеличивать эту стоимость, и, следовательно, имущественную составляющую бюджета.

Массовая оценка обычно выполняется в государственных целях, в том числе определение налогооблагаемой базы для объектов недвижимости;

Данная работа посвящена массовой оценке недвижимости в целях налогообложения на примере некоторых городов Ярославской области, а так же построению регрессионной модели для оценки стоимости жилой недвижимости.

Для достижения поставленной цели в данной работе нами были реализованы следующие задачи:

• изучение принципов, стандартов и подходов к оценке недвижимости в налогообложении;

• изучение математических методов статистического моделирования и массовой оценки недвижимого имущества;

• рассмотреть этапы построения эконометрической модели стоимости жилой недвижимости;

• разработать регрессионную модель стоимости жилой недвижимости в целях налогообложения на основе анализа рынка недвижимости Ярославской области.

При рассмотрении теоретические и методологических основ оценки недвижимости для налогообложения был, сделан вывод о том, что основной целью оценки для налогообложения является определение налоговой стоимости объекта на базе его рыночной стоимости. Это означает, что при отсутствии погрешности измерения последней, налоговая стоимость могла бы быть приравнена к рыночной стоимости. На практике рыночная стоимость может быть определена методами массовой оценки с конечной точностью.

Наиболее верным подходом к массовой оценке жилой недвижимости в целях налогообложения из трёх существующих является сравнительный подход, так как он в силу хорошо развитой системы информационного обеспечения даёт наиболее объективные результаты.

С помощью эконометрического моделирования нами была построена регрессионная модель оценки стоимости жилой недвижимости в зависимости от ценооборазующих факторов. Для этого нами была составлена статистическая совокупность на основе анализа вторичного рынка жилой недвижимости на примере некоторых городов Ярославской области: Ярославль, Рыбинск, Тутаев, Углич.

В ходе построения модели, оказалось, что наибольшее влияние на стоимость жилой недвижимости оказывает этажность, общая площадь жилья, площадь кухни, состояние жилой недвижимости, престижность района, удаленность от областного центра и уровень застройки в регионе.

Отметим, что ценообразующие факторы, выявленные для рынка жилой недвижимости Ярославской области, не являются универсальными, а каждый рынок имеет свои специфические особенности.

В результате, нами была получена модель расчета стоимости жилой недвижимости следующего вида:

Мы провели проверку полученной модели на примере однокомнатной квартиры в городе Ярославле с использованием тех же ценообразующих факторов, используемых при построении модели. В результате проверки расчетное значение незначительно отличалось от цены предложения данной квартиры на рынке.

Следовательно, данная модель дает возможность оценить объекты, не только для тех, к которым невозможно для оцен­ки стоимости всех объектов, анализируемые характеристики которых пре­дусмотрены в модели в Ярославской области. Также эту модель можно использовать для массовой оценки жилой недвижимости в целях налогообложения.

Список использованных источников

1. Гражданский кодекс Российской Федерации. Части первая, вторая и третья. – М.: ТК Велби, Изд-во Проспект, 2005. – 448 с.

2. Федеральный закон «Об оценочной деятельности в Российской Федерации» N135-ФЗ от 29.07.98 (в редакции Федерального закона N 220-ФЗ от 24.07.07)

3. ФСО-1: Приказ Минэкономразвития России «Общие понятия оценки, подходы к оценке и требования к проведению оценки (ФСО N 1)» от 20 июля 2007 года N 256

4. ФСО-2: Приказ Минэкономразвития России «Цель оценки и виды стоимости (ФСО N 2)» от 20 июля 2007 года N 255

5. ФСО-3: Приказ Минэкономразвития России «Об утверждении федерального стандарта оценки "Требования к отчету об оценке (ФСО N 3)» от 20 июля 2007 года N 254

6. ФСО-4: Приказ Минэкономразвития России «Определение кадастровой стоимости (ФСО N 4)» от 22 октября 2010 года N 508;

7. ФСО-5: Приказ Минэкономразвития России «Виды экспертизы, порядок ее проведения, требования к экспертному заключению и порядку его утверждения (ФСО N 5)» от 4 июля 2011 года N 238;

8. ФСО-6: Приказ Минэкономразвития России «Требования к уровню знаний эксперта саморегулируемой организации оценщиков (ФСО N 6)» от 7 ноября 2011 года N 628.

9. СТО РОО 20-06-96. Классификатор услуг по оценке имущества. Стандарт Российского общества оценщиков. – М.:РОО, 1996

10. Асаул А. Н. «Экономика недвижимости» – СПб.: Питер, 2007 г.

11. Айвазян С.А., Мхитарян В.С. «Прикладная статистика и основы эконометрики». – М.: «Юнити», 1998

12. Бабенко Р.В. «Оценка стоимости жилой недвижимости» Ростов н/Д: «Росиздат», 2005.

13. Бабешко Л.О. «Основы эконометрического моделирования» – М.: КомКнига, 2007 г.

14. Булгаков С.Н., Наназашвили И.Х., Мирошниченко А.С., Дарков А.К. «Система экспертиз и оценка объектов недвижимости» – М.: Архитектура С, 2007 г.

15. Виноградов Д.В. «Экономика недвижимости», уч. П. Владимирский гос. университет, 2007.

16. Грибовский С.В. «Массовая оценка недвижимости в целях налогообложения» – СПб.: Питер, 2011

17. Грибовский С.В., Иванова Е.Н., Львов Д.С., Медведева О.Е. М. «Оценка стоимости недвижимости» – СПб: «Интерреклама», 2004.

18. Грибовский С.В., С.А. Сивец «Математические методы оценки стоимости недвижимого имущества», - М.: «Финансы и статистика», 2009

19. Грязнова А.Г., Федотова М.А. «Оценка недвижимости» – М.: Финансы и статистика, 2009 г.

20. Елисеев В.М. Классификация видов стоимости. – Вопросы оценки, № 1’98.

21. Зимин А. И. «Оценка имущества. Вопросы и ответы» – М.: Юриспруденция , 2007 г.

22. Иванова Е.Н. «Оценка стоимости недвижимости» – М.: КноРус, 2008 г.

23. Каминский А. В., Страхов Ю. И., Трейгер Е. М. «Анализ практики оценки недвижимости» – М.: РИО МАОК, 2005 г..

24. Микерин Г.И., Гребенников В.Г., Нейман Е.И. «Методологические основы оценки стоимости имущества.» М. : ИНТЕРРЕКЛАМА, 2003.

25. Наназашвили И. Х. , Литовченко В. А. «Оценка недвижимости» М.: Архитектура-С, 2005 г.

26. Орлов С. В., Цыпкин Ю. А. «Рыночная оценка имущества города» – М.: Юнити-Дана, 2002 г.

27. Севостьянов А. В. «Экономическая оценка недвижимости и инвестиции» – М.: Академия, 2008 г.

28. Сивец С.А. «Построение и практическое применение многофакторной гибридной модели оценки доходной недвижимости» – Вопросы оценки. – 2001.

29. Сивец С.А., Левыкина И.А. «Эконометрическое моделирование в оценке недвижимости», Запорожье: «Полиграф», 2003.

30. Склярова Е. Н. «Основы оценки стоимости недвижимости» - М.: РИО МАОК, 2004 г.

31. Соловьев М. М. «Оценочная деятельность» – М.: ГУ ВШЭ, 2002 г.

32. Тэпман Л. Н. «Оценка недвижимости. Учебное пособие для вузов» – М.: Юнити-Дана, 2005 г.

33. Федотова М.А., Рослов В.Ю., Щербакова О.Н., Мышанов А.И. «Оценка для целей залога, теория, практика, рекомендации» – М.: «Финансы и статистика».

34. Федотова М.А., Уткин Э.А. Оценка недвижимости и бизнеса. – М.: «ЭКМОС», 2010 г.

35. Шевчук Д. А. «Оценка недвижимости и управление собственностью» М.: Феникс, 2007 г.

36. http://www.ststatisticworld.ru

37. http://bicenter.info/articles/12.shtml

38. http://www.infamed.com/stat/s05.html