2.2 Этапы построения эконометрической модели стоимости жилой недвижимости

Разработка модели и исследование экономических процессов осуществляется в несколько этапов. Рассмотрим подробнее содержание этапов:

1. Формирование перечня факторов и их логический анализ.

Для определения наиболее разумного числа переменных в регрессионной модели прежде всего ориентируются на соображения профессионально-теоретического характера. Исходя из физического смысла явления, производят классификацию переменных на зависимую и объясняющую.

Изменение стоимости любой недвижимости зависит от целого ряда факторов, которые проявляются на различных стадиях процесса оценки. Все факторы, влияющие на стоимость недвижимости, можно разделить на объективные и субъективные. При этом последние связаны с поведением конкретного продавца, покупателя или посредника на стадии заключения сделки (например, осведомленность, честность, темперамент, личные симпатии и т.д.), т.е. факторы в основном психологического характера.

Как правило, объективные факторы - это экономические факторы, которые определяют средний уровень цен конкретных сделок субъектами недвижимости. Их можно разделить на:

• макроэкономические – факторы, связанные с общей конъюнктурой рынка (налоги, пошлины, динамика курса доллара, инфляция, безработица, уровень и условия оплаты труда, потребность в объектах недвижимости, развитие внешнеэкономической деятельности и т.д.);

•  микроэкономические – факторы, характеризующие объективные параметры конкретных сделок, связаны с описанием объекта купли-продажи недвижимости и с правовым характером сделки.

К субъективным факторам, связанным с феноменом массового сознания и факторы психологического характера относятся:

•  массированная реклама;

•  инфляционные ожидания;

•  симпатии;

•  осведомленность и т.д.

Для краткосрочных периодов макроэкономические факторы можно считать условно-постоянными (они изменяются довольно медленно), а общую конъюнктуру рынка – фиксированной.

Для того чтобы определить стоимость объекта недвижимости, необходимо иметь представление о совокупности факторов, влияющих на стоимость недвижимости, а также о влиянии каждого конкретного фактора.

Рассмотрим основные факторы, влияющие на стоимость недвижимости.

Физические факторы:

1. местоположение (напрямую влияет на стоимость недвижимости):

• по отношению к деловому центру, местам приложения труда, жилым территориям, автодороге, железной дороге, побережью, зеленым массивам, коммунальным учреждениям (свалкам и т.п.);

• наличие и состояние коммуникаций;

• наличие объектов социально-культурного назначения;

• размещение объектов в плане города (района), примыкающее окружение.

2. физические характеристики:

• физические параметры: площадь, размеры, форма, материал постройки, год постройки или реконструкции, этажность и др.;

• качество строительства и эксплуатации;

• наличие коммунальных услуг (электроэнергия, водоснабжение, теплосеть и др.) – если коммуникации не подключены, при оценке необходимо подсчитать расходы на их подключение;

• функциональная пригодность;

• привлекательность, комфорт;

3. архитектурно-конструктивные решения – в зависимости от назначения дальнейшего использования здания стоимость его будет увеличиваться или уменьшатся:

• стиль, планировка, конструкции и т. д.;

• объемно-планировочные показатели и др.;

4. состояние объекта недвижимости – если для ремонта здания необходимо истратить значительное количество денег, покупатель вычтет данные затраты из стоимости сделки, однако если требуется только косметический ремонт, это существенно не повлияет на стоимость недвижимости;

5. экологические и сейсмические факторы (для жилой недвижимости данные санитарно-экологической экспертизы могут значительно снизить стоимость жилья, а наличие лесопарковой зоны, водоемов, парков и пр. может увеличить стоимость квартир).

Экономические факторы:

1. общие: общее состояние мировой экономики, экономическая ситуация в стране, регионе, на местном уровне, финансовое состояние предприятий;

2. факторы спроса: уровень занятости, уровень доходов и тенденции его изменения, платежеспособность, доступность кредитных ресурсов, ставки процента и арендной платы, издержки при формировании продаж, обеспеченность населения объектами общественного назначения и др.;

3. факторы предложения: наличие источников и условия финансирования строительства и реконструкции, число объектов, выставленных на продажу; затраты на строительно-монтажные работы и тенденция их изменения, налоги.

Социальные факторы:

1. базовые потребности в приобретении объектов недвижимости, в варианте их использования; базовые потребности в общении с окружающими, отношение к соседним объектам и их владельцам, чувство собственности;

2. тенденции изменения численности населения, его омоложения или старения, размер семьи, плотность заселения, др.;

3. тенденции изменения образовательного уровня, уровня культуры, уровня преступности;

4. стиль и уровень жизни.

Политические (административные) факторы:

1. политическая стабильность, безопасность;

2. налоговая политика, финансовая политика, предоставление разного рода льгот;

3. зонирование: запретительное, ограничительное или либеральное;

4. строительные нормы и правила: ограничительные или либеральные;

5. услуги муниципальных служб: дороги, благоустройство, инженерное оборудование, общественный транспорт, школы, противопожарная служба;

6. наличие и совершенство законодательства (об ипотеке, о собственности, об операциях с недвижимостью, в области экологии, о залоге, в области строительства, о кредитной политике и др.), лицензирование риэлтерской и оценочной деятельности.

В модель оценки объектов недвижимости для целей налогообложения следует включать факторы, имеющие наивысшую степень корреляции с ценой объекта. Приемлемую точность можно получить даже при трех-четырех факторах: местоположение, категория дома, количество комнат в квартире и этаж квартиры. Для каждого поселения набор факторов может быть свой.

Важнейшим ценообразующим фактором, который необходимо учитывать при оценке недвижимости для налогообложения является местоположение. Исследования показывают, что этот фактор на 70-80 % определяет цену объекта недвижимости [19].

2. Априорное исследование экономической проблемы.

На этом этапе исследования должны быть сформулированы экономически осмысленные и приемлемые гипотезы о зависимости экономических явлений.

Проверка данных на соответствие нормальному закону распределения можно провести с помощью:

1. Коэффициента вариации.

Проверку гипотезы о нормальном законе распределении, как правило, начинают с вычисления коэффициента вариации по формуле:

(2.8)

Если значение коэффициента вариации превышает 33%, то гипотеза о нормальном распределении данных выборки не подтверждается. При этом, дальнейшую проверку по другим критериям проводить уже не целесообразно. Если же условие выполняется, необходимо продолжить проверку по остальным критериям.

2. Критерия среднего абсолютного отклонения.

Для выборок, объем которых не превышает 120 объектов, для проверки гипотезы о нормальном законе распределения используется показатель среднего абсолютного отклонения, определяемый как:

(2.9)

Для выборки, имеющей приближенно нормальный закон распределения, должно выполняться соотношение:

(2.10)

Проверка модели на наличие выбросов

При анализе выборочных данных исследователь, в частности оцен­щик, часто сталкивается с проблемой, когда отдельные значения ряда существенно отличаются от общей массы умеренно различающихся дан­ных. Такие значения называются выбросами и, как правило, они долж­ны быть исключены из выборки.

Чаще всего такие отклонения связаны с ошибками, возможно, имев­шими место при формировании выборки, а именно ошибками при из­мерениях или расчетах. К причинам, объясняющим появление выбро­сов также можно отнести включение в выборку объектов с резко отличающимися характеристиками, т.е. принадлежащих другой генераль­ной совокупности. Например, в практике оценки появление в данных выбросов может объясняться наличием в выборке рыночных данных, принадлежащих другому, как правило, смежному, сегменту рынка (дру­гому классу объектов, другому региону и т.д.). И если не анализировать выборку на наличие выбросов, то это может привести к ошибочны выводам, как по оценкам параметров, так и по различным проверяемы статистическим гипотезам.

В статистике существует следующее общее правило: "Интервал трех сигм (х±3 ) включает в себя при нормальном распределении 99,9% значений". Следовательно, значения, не попавшие в интервал, можно рассматривать как потенциальные выбросы. Процедура выявления выб­росов не должна носить субъективный характер. Существует ряд методов, позволяющих определить, является или нет экстремальное значе­ние выбросом для данной выборки. Мы рассмотрим два из них, применение которых зависит от объема выборки. Другие критерии проверки на наличие выбросов подробно рассматриваются в специализи­рованных статистических изданиях.

Для выборок объемом n ≤ 25 процедура проверки экстремальных зна­мений на предмет их исключения из выборки как выбросов на основе вариационного ряда осуществляется с помощью М-критерия по следу­ющему алгоритму.

Пусть x_min = х₁ - экстремальное значение, которое предположитель­но рассматривается как выброс (если на выброс требуется проверить x_max, то элементы вариационного ряда необходимо перенумеровать в порядке убывания, и тогда x_max = х₁).

Далее определяем расчетное значение М_расч, которое сравнивается с критическим значением М из таблицы 5. В этой же таблице приведены выражения, по которым рассчитывается М_расч в зависимости от объема выборки. Если М_расч < М, то экстремальное значение х₁ с вероятностью 1-α не является выбросом, т.е. его нельзя исключать из выборки. В таких случаях экстремальное значение объясняется проявлением изменчивости, характерной для данной генеральной совокупности. Если же выполняется неравенство М_расч ≥ М, то считается, что проверяемое экстремальное значение принадлежит к другой генеральной совокупности и для данного ряда значений является выбросом.

При объемах выборки n > 25 экстремальные значения могут быть проверены на основании критерия Смирнова—Граббса:

, (2.11)

где – оценки, рассчитанные по данным всей выборки;

х₁ - экстремальное значение – подозреваемый выброс.

Критические значения данного критерия S определяются по таблица 4 в соответствии с объемом выборки n и заданным уровнем значимо­сти α.

Если S_расч < S, то подозрение, что экстремальное значение х₁, является выбросом, с вероятностью 1-α отклоняется, В противном случае, т.е. когда S > S, можно считать, что значение х₁ является выбросом. Тогда необходимо исключить соответствующие выбросу данные из выборки и построить новую модель, не используя исключенных данных

Таблица 4

Критические значения S-критерия

Объем выборки, n	Уровень значимости
	α=0,05	α=0,01
1	1,645	2,326
2	1,955	2,575
3	2,121	2,712
4	2,234	2,806
5	2,319	2,877
6	2,386	2,934
8	2,49	3,022
10	2,568	3,089
15	2,705	3,207
20	2,799	3,289
30	2,929	3,402
50	3,082	3,539
100	3,283	3,718
1000	3,884	4,264

Таблица 5

Таблица критических значений М

Объем выборки, n	Уровень значимости			Мрасч
	α=0,10	α=0,05	α=0,01
3	0,866	0,941	0,988
4	0,679	0,765	0,889
5	0,557	0,642	0,78
6	0,482	0,56	0,698
7	0,434	0,507	0,637
8	0,479	0,554	0,683
9	0,441	0,512	0,635
10	0,409	0,477	0,597
11	0,517	0,576	0,679
12	0,49	0,546	0,642
13	0,467	0,521	0,615
14	0,492	0,546	0,641
15	0,472	0,525	0,616
16	0,454	0,507	0,595
17	0,438	0,409	0,577
18	0,424	0,475	0,561
19	0,412	0,462	0,547
20	0,401	0,45	0,535
21	0,391	0,44	0,524
22	0,382	0,43	0,514
23	0,374	0,421	0,505
24	0,367	0,413	0,497
25	0,36	0,406	0,489

Критические значения данного критерия S определяются по таблица 4 в соответствии с объемом выборки n и заданным уровнем значимо­сти α.

Если S_расч < S, то подозрение, что экстремальное значение х₁, является выбросом, с вероятностью 1-α отклоняется, В противном случае, т.е. когда S > S, можно считать, что значение х₁ является выбросом. Тогда необходимо исключить соответствующие выбросу данные из выборки и построить новую модель, не используя исключенных данных.

3. Сбор исходных данных и их первичная обработка.

При создании модели какого-либо сектора рынка рекомендуется определять ее параметры на данных, максимально отражающих вариацию влияющих признаков в общей (генеральной) совокупности объектов моделируемого сектора рынка. Кроме того, очевидным является то, что минимизация суммарной погрешности моделирования (остаточной суммы квадратов), прежде всего, обеспечивается минимизацией ошибок модели для наиболее часто встречающихся объектов, входящих в совокупность объекта моделирования. Отсюда следует необходимость обладания информацией о структуре параметров генеральной совокупности объекта моделирования и использования ее при планировании эксперимента по исследованию рынка.

Анализ объекта моделирования преследует две связанные между собой цели:

• определение параметров генеральной совокупности моделируемых объектов недвижимости для построения адекватной модели рынка методом массовой оценки;

• оптимизация плана эксперимента по формированию репрезентативной выборки ценовых рыночных данных об объектах, аналогичных объектам исследования.

Немаловажной характеристикой объекта недвижимости, влияющей на ценообразование, является его функциональное назначение, понимаемое как наилучшее и наиболее эффективное использование. Использование объекта не только является основным классифицирующим признаком, но и определяет состав основных ценообразующих признаков. В связи с этим представляет интерес распределение исследуемых объектов недвижимости (объектов моделирования) по функциям использования в общегородском и в районном разрезе. Также необходимо проанализировать распределение площади объектов недвижимости в том же разрезе по основным ценообразующим факторам, которые предполагается учитывать в модели (например, занимаемым этажам, площади помещения, типу здания, типу входа в помещение, техническому состоянию помещений, уровню благоустройства и другим характеристикам).

Методика сбора и состав рыночной информации напрямую зависят от назначения модели.

Каждое направление выбора информации имеет свои преимущества, сочетание которых позволяет добиться высокого качества исходной информации.

Информация о сделках и предложениях является основой построения модели рынка. Именно на основе такой информации и характеристиках объектов определяется общий вид зависимости цены объекта от его физических характеристик и условий проведения сделки. Непосредственный сбор информации о сделках и предложениях на рынке от арендодателей позволяет выяснить все условия аренды предлагаемого помещения, получить наиболее полную и унифицированную информацию о характеристиках объекта и его окружения, поэтажные планы и фотографии объекта, выявить дополнительные ценообразующие факторы, условия оплаты и т. п.

При построении модели исходная информация может быть собрана в трех видах:

• динамические (временные) ряды;

• пространственная информация — информация о работе нескольких объектов в одном разрезе времени;

• сменная — табличная форма. Информация о работе нескольких объектов за разные периоды.

Объем выборки зависит от числа факторов, включаемых в модель с учетом свободного члена. Для получения статистически значимой модели требуется на один фактор объем выборки, равный 5 - 8 наблюдений. Например, если в модель включаются три фактора, то минимальный объем выборки:

n_min = 5 (m+n) = 5 (3 + 1) = 20, (2.12)

где т — число факторов, включаемых в модель;

п — число свободных членов в уравнении.

Если в квартальном разрезе собирать данные, то надо брать информацию за 5 лет.

4. Спецификация функции регрессии.

На данном этапе исследования дается конкретная формулировка гипотезы о форме связи (линейная или нелинейная, простая или множественная и т. д.). Для этого используются различные критерии для проверки состоятельности гипотетического вида зависимости. На этом этапе проверяются предпосылки корреляционно-регрессионного анализа.

5. Оценка функции регрессии.

Здесь определяются числовые значения параметров регрессии и вычисление ряда показателей, характеризующих точность регрессионного анализа.

6. Отбор главных факторов.

Выбор факторов - основа для построения многофакторной корреляционно-регрессионной модели.

На этапе формирования перечня факторов и их логического анализа собираются все возможные факторы, обычно более 20–30 факторов. Но это неудобно для анализа, и модель, включающая 20–30 факторов, будет неустойчива. Неустойчивость модели находит выражение в том, что в ней изменение некоторых факторов ведет к увеличению у вместо снижения y.

Мало факторов – тоже плохо. Это может привести к ошибкам при принятии решений в ходе анализа модели. Поэтому необходимо выбирать более рациональный перечень факторов. При этом проводят анализ факторов на мультиколлинеарность.

Мультиколлинеарность – попарная корреляционная зависимость между факторами. Мультиколлинеарная зависимость присутствует, если коэффициент парной корреляции .

Отрицательное воздействие мультиколлинеарности состоит в следующем:

1) усложняется процедура выбора главных факторов;

2) искажается смысл коэффициента множественной корреляции (он предполагает независимость факторов);

3) усложняются вычисления при построении самой модели;

4) снижается точность оценки параметров регрессии, искажается оценка дисперсии.

Следствием снижения точности является ненадежность коэффициентов регрессии и отчасти неприемлемость их использования для интерпретации как меры воздействия соответствующей объясняющей переменной на зависимую переменную.

Оценки коэффициента становятся очень чувствительными к выборочным наблюдениям. Небольшое увеличение объема выборки может привести к очень сильным сдвигам в значениях оценок. Кроме того, стандартные ошибки оценок входят в формулы критерия значимости, поэтому применение самих критериев становится также ненадежным. Из сказанного ясно, что исследователь должен пытаться установить стохастическую мультиколлинеарность и по возможности устранить ее.

Для измерения мультиколлинеарности можно использовать коэффициент множественной детерминации R2, где R – коэффициент множественной корреляции.

При отсутствии мультиколлинеарности факторов:

(2.13)

где d_yj — коэффициент парной детерминации, вычисляемый по формуле:

(2.14)

где r_yj — коэффициент парной корреляции между j-м фактором и зависимой переменной у.

При наличии мультиколлинеарности соотношение не соблюдается. Поэтому в качестве меры мультиколлинеарности используется следующая разность:

(2.15)

Чем меньше эта разность, тем меньше мультиколлинеарность.

Для устранения мультиколлинеарности используется метод исключения переменных. Этот метод заключается в том, что высоко коррелированные объясняющие переменные (факторы) устраняются из регрессии и она заново оценивается. Отбор переменных, подлежащих исключению, производится с помощью коэффициентов парной корреляции. Опыт показывает, что если , то одну из переменных можно исключить, но какую переменную исключить из анализа, решают исходя из управляемости факторов на уровне предприятия.

Обычно в модели оставляют тот фактор, на который можно разработать мероприятие, обеспечивающее улучшение значения этого фактора в планируемом году. Возможна ситуация, когда оба мультиколлинеарных фактора управляемы на уровне предприятия. Решить вопрос об исключении того или иного фактора можно только в соответствии с процедурой отбора главных факторов.

Отбор факторов не самостоятельный процесс, он сопровождается построением модели. Принятие решения об исключении факторов производится на основе анализа значений специальных статистических характеристик и с учетом управляемости факторов на уровне предприятия.

Оценка параметров конкретного уравнения регрессии является лишь отдельным этапом длительного и сложного процесса построения рег­рессионной модели. Первое же полученное уравнение очень редко яв­ляется удовлетворительным во всех отношениях. Обычно приходится постепенно подбирать форму связи и состав факторных переменных, т.е. возвращаться к этапу спецификации модели, анализи­руя каждый раз качество полученной модели. Четкого критерия прекращения итераций нет. Здесь, как, впрочем, в любом другом анализе, следует руководствовать­ся логикой и здравым смыслом. Необходимо останавли­ваться на той итерации, когда становится очевидным, что следующая итерация не даст существенного прироста скорректированного коэф­фициента детерминации, о значении которого будет рассказано несколько позже. Показатели качества, представленные ниже, как раз и являются статистическими оценками точности результатов регрессионной моде­ли, и если оценщик применил в своей работе по оценке имущества такую модель, то нет ничего лучшего, как изложить в отчете об оценке убедительные, подтвержденные статистическими данными, суждения о точности полученных результатов.

Рассмотрим наиболее часто используемые показатели качества множественной линейной регресси­онной модели.

1. Стандартное отклонение ошибки:

. (2.16)

Этот показатель можно также назвать среднеквадратическим откло­нением оценки. Стандартное отклонение результата 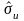измеряет величи­ну отклонения фактических значений результирующего показателя у от соответствующих расчетных значений , полученных с помощью рег­рессионной модели. При этом можно утверждать, что 68% реальных значений результирующего показателя у находятся в диапазоне ± линии регрессии, а 95% — в диапазоне ±2 . Единицы измерения совпадают с единицами измерения результирующего признака у.

2. Коэффициент вариации результирующего признака:

. (2.17)

В регрессионном анализе коэффициент вариации представляет собой стандартное отклонение результата, выраженное в виде процент­ного отношения к среднему значению результирующего показателя. Коэффициент вариации может служить критерием прогнозных качеств полученной регрессионной модели: чем меньше величина , тем более высокими являются прогнозные качества модели. Использование коэффициента вариации предпочтительнее показателя , так как он яв­ляется относительным показателем. При практическом использовании данного показателя рекомендуют — не применять модель, коэффициент вариации которой превышает 33%.

3. Коэффициент детерминации (квадрат коэффициента множественной корреляции):

. (2.18)

Данный показатель используется для анализа общего качества полу­ченной регрессионной модели. Он указывает, какой процент вариации у объясняется влиянием всех включенных в модель факторных пере­менных. Коэффициент детерминации всегда лежит в интервале от 0 до 1. Чем ближе значение коэффициента детерминации к 1, тем лучше модель описывает исходный ряд данных.

Точную границу приемлемости показателя R² для всех случаев указать невозможно. Нужно принимать во внимание и объем выборки, и содержательную интерпретацию уравнения. Как правило, при исследо­вании данных об однотипных объектах, полученных примерно в один и тот же момент времени, величина R² не превышает уровня 0,6—0,7 [6]. Только в случае, если все ошибки прогнозирования равны 0, т.е. когда связь между факторными переменными и результирующим показателям является функциональной, R² = 1.

4. Скорректированный коэффициент детерминации:

. (2.19)

Необходимость введения скорректированного коэффициента детер­минации объясняется тем, что при увеличении числа переменных k обыч­ный коэффициент детерминации практически всегда увеличивается, но уменьшается число степеней свободы (n-k-1). Введенная корректи­ровка всегда уменьшает значение R², поскольку (n-1) > (n-k-1). В результате величина даже может стать отрицательной. Это озна­чает, что величина R² была близка к 0 до корректировки и объясняемая с помощью уравнения регрессии доля дисперсии переменной у очень мала.

Из двух вариантов регрессионных моделей, которые отличаются ве­личиной скорректированного коэффициента детерминации, но имеют одинаково хорошие другие критерии качества, предпочтительнее вари­ант с большим значением скорректированного коэффициента детерми­нации.

5. Средняя ошибка аппроксимации (среднее процентное отклоне­ние) вычисляется как средняя относительная разность (выраженная в процентах) между фактическими и расчетными значениями результи­рующего показателя:

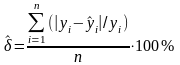. (2.20)

Средняя ошибка аппроксимации отражает свойства модели по воспроизведению исходных рыночных данных. Естественно, чем меньше значение данного показателя, тем луч­ше прогнозные качества модели. В таблице 2.6 приведена характеристика точности модели в зависимости от значения данного показателя.

Таблица 6

Характеристики точности регрессионных моделей по уровню средней ошибки аппроксимации

Значение , %	Характеристика точности модели
До 7	Высокая точность
7-12	Хорошая точность
12-15	Удовлетворительная точность
Свыше 15	Неудовлетворительная точность

7. Проверка значимости уравнения регрессии в целом проводится с помощью F-критерия. Эта процедура сводится к проверке статистичес­кой значимости коэффициента детерминации R², т.е. проверяется нуле­вая гипотеза R² = 0. Эта гипотеза равносильна гипотезе , т.е. ни одна из факторных переменных, включенных в регрессион­ную модель, не оказывает существенного влияния на результирующий показатель. Смысл проверяемой гипотезы заключается в том, что все коэффициенты линейной регрессии, за исключением свободного чле­на, равны 0. Если они действительно равны нулю для генеральной совокупности, то уравнение регрессии должно иметь вид , а коэффи­циент детерминации R² должен быть равен 0. Если коэффициент R² значим, следовательно, связь меж­ду у и факторными переменными 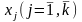действительно существует и можно приступать к ее объяснению. Если же коэффициент R² незначим, то данные представляют собой набор не связанных между собой случайных чисел. Однако это еще не значит, что зависимости нет, возможно, просто исходных данных не достаточно для того, чтобы она про­явилась. Расчетное значение F-критерия определяется по формуле:

(2.21)

При традиционном способе проверки F-критерия значение F_расч срав­нивается с критическим значением F_крит при заданном уровне значимости и числе степеней свободы: m₁=k и m₂=n-k-1. Если расчетное зна­чение превышает критическое, т.е. F_pacч > F_крит, то гипотеза о несоот­ветствии заложенных в уравнение регрессии связей реально существую­щим отвергается, и говорят, что уравнение в целом статистически значимо, что означает хорошее соответствие данным наблюдениям.

7. Проверка статистической значимости параметров уравнения рег­рессии проводится с помощью F-критерия (критерия Стьюдента). Оце­нить статистическую значимость коэффициента регрессии означает определиться, существенно ли влияет факторная переменная х_j в гене­ральной совокупности на результирующую переменную у, т.е. отличает­ся ли истинное (но неизвестное) значение коэффициента от 0. Для статистической проверки этой гипотезы применяется t-критерий.

Расчетное значение t-критерия вычисляется по формуле:

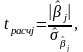(2.22)

где — среднеквадратическое отклонение для коэффициента .

При вычислениях в MS Excel таблицах регрессионного анализа содержатся значения t_{расч j} (так называемая «t-статистика») для всех коэффициентов уравнения регрессии, а также соответствующие значения доверитель­ных вероятностей (так называемые «Р-значения»).

При традиционном способе проверки t-критерия каждое значение t_{расч j}, сравнивается с критическим значением t_крит при заданном уровне значимости α и числе степеней свободы m=n-k-1. Если выполняется неравенство t_{расч j} > t_крит, то гипотеза о том, что коэффициент является статистически незначимым отвергается. Таким образом, в данном слу­чае есть основание полагать, что х_j является значимой переменной при прогнозировании величины результирующего показателя у. Напротив, если выполняется неравенство t_{расч j} ≤ t_крит, то нельзя отвергнуть предпо­ложение, что равно 0 и что х_j является несущественной переменной для объяснения у. Однако следует подчеркнуть, что это еще не означа­ет, что х_j вовсе никак не связана с у. Критерий Стьюдента измеряет предельный вклад переменной в прогноз у при фиксировании других факторных переменных уравнения регрессии. Поскольку некоторые переменные могут дублировать информацию, уже учтенную за счет дру­гих переменных (наблюдается мультиколлинеарность в данных), они могут сильно коррелировать с величиной у, однако являться несуще­ственными для прогноза, на что указывает соответствующее расчетное значение t-критерия [15].
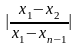
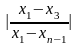
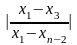