Глава 2 Особенности использования статистических и математических методов в оценке с целью налогообложения

2.1 Применение эконометрических моделей в массовой оценке недвижимости

Задача создания модели рынка оцениваемого объекта при наличии информации должна решаться методами статистического анализа рынка недвижимости. Модель оценки создается на базе некоторого числового материала. Таким материалом является рыночная ценовая и техническая информация об объектах недвижимости. Следовательно, активный рынок можно определить как рынок объекта недвижимости, имеющий достаточный объем информации для его оценки статистическими методами. Достаточным следует признать такую выборочную совокупность, которая обладала бы свойствами всей (генеральной) совокупности объектов недвижимости на оцениваемой территории, т.е. в этой выборочной совокупности присутствовали бы в статистически значимом количестве представители всех типов объектов оценки.

На современном этапе развития методик массовой оценки в России наибольшее распространение получила общепринятая в мировой практике методология корреляционно - регрессионного моделирования (КРМ). Указанная методология предполагает построение статистических моделей, описывающих количественную зависимость исследуемого результирующего признака (стоимость, ставка аренды) от характеристик (влияющих признаков, ценообразующих факторов) объектов-аналогов, для которых известна рыночная ценовая информация.

Понятия «корреляция» и «регрессия» тесно связаны между собой. Корреляция означает соотношение между объективно существующими явлениями. Связи между явлениями могут быть различны по силе. При измерении тесноты связи говорят о корреляции в узком смысле слова. Если случайные переменные причинно обусловлены и можно в вероятностном смысле высказаться об их связи, то имеется корреляция.

В корреляционном анализе оценивается сила связи, а в регрессионном анализе исследуется ее форма. Корреляция в широком смысле объединяет корреляцию в узком смысле и регрессию.

Любое причинное влияние может выражаться либо функциональной, либо корреляционной связью. Но не каждая функция или корреляция соответствует причинной зависимости между явлениями. Поэтому требуется обязательное исследование причинно-следственных связей.

Исследование корреляционных связей мы называем корреляционным анализом, а исследование односторонних стохастических зависимостей — регрессионным анализом. Корреляционный и регрессионный анализ имеют свои задачи.

Однако в практическом применении метода КРМ для массовой оценки стоимости недвижимости существует ряд методических недостатков, которые существенно усложняют достижение конечного результата, а также вносят большую субъективность в оценку стоимости. Основными недостатками применения регрессионных моделей и методов при решении задач оценки сравнительным подходом являются:

1. контролируемый характер (подборка параметров объектов — аналогов, направленных на результат);

2. в методе КРМ гипотезу о нормальности распределения выборки рыночных данных нельзя рассматривать как принимаемую автоматически, и требуется проверка специальными предусмотренными процедурами. Как правило, обеспечение отсутствия в выборке грубых погрешностей и нормальность ее распределения в методе КРМ приводит к отсечению предложений по элитной недвижимости.

3. для метода КРМ нежелательно введение большого числа факторов, так как они чаще всего оказываются незначимыми, следует отбирать факторы, находящиеся в тесной корреляционной связи с выбранным результирующим показателем.

Корреляционный анализ – это совокупность методов исследования параметров многомерного признака, позволяющая по выборке из генеральной совокупности сделать статистические выводы о мерах статистической зависимости между компонентами исследуемого признака.

Виды корреляций

Корреляция, как и регрессия, имеет различные виды, так различают:

1) относительно характера

• положительную;

• отрицательную;

2) относительно числа переменных

• простую;

• множественную;

• частную;

3) относительно формы связи

• линейную;

• нелинейную;

4) относительно типа соединения

• непосредственную;

• косвенную;

• ложную.

Регрессия - вероятностная зависимость среднего значения случайной величины от некоторой другой величины или нескольких величин.

Виды регрессий

1. Регрессия относительно числа переменных:

• простая регрессия — регрессия между двумя переменными;

• множественная регрессия — регрессия между зависимой переменной у и несколькими объясняющими переменными х₁, x₂, ...,x_m.

2. Регрессия относительно формы зависимости:

• линейная регрессия, выражаемая линейной функцией;

• нелинейная регрессия, выражаемая нелинейной функцией.

3. В зависимости от характера регрессии различаются следующие ее виды:

• положительная регрессия: она имеет место, если с увеличением (уменьшением) объясняющей переменной значения зависимой переменной также соответственно увеличиваются (уменьшаются);

• отрицательная регрессия: в этом случае с увеличением или уменьшением объясняющей переменной зависимая переменная уменьшается или увеличивается.

4. Относительно типа соединения явлений различаются:

• непосредственная регрессия: в этом случае зависимая и объясняющая переменные связаны непосредственно друг с другом;

• косвенная регрессия: в этом случае объясняющая переменная действует на зависимую через ряд других переменных;

• ложная регрессия: она возникает при формальном подходе к исследуемым явлениям без уяснения того, какие причины обусловливают данную связь.

При построении регрессионной модели необходимо решить следующие задачи:

1. Преобразовать качественные факторы в количественные.

Проблема перевода качественных переменных в количественные особенно актуальна при построении регрессионных моделей для целей оценки стоимости, поскольку большинство ценообразующих факторов относится к качественным показателям (характеристика района (обеспеченность объектами социальной инфраструктуры, удаленность от центра, обеспеченность общественным транспортом, экологическая обстановка, удобство подъезда); параметры квартала (состояние прилегающей территории, объекты промышленной инфраструктуры, характеристика дома, материал стен,, материал перекрытий, коммуникации, привлекательность дома, состояние двора, домофон); характеристика квартиры (планировка комнат, санузел, балкон или лоджия, дополнительные системы безопасности, ориентация окон, уровень отделки, состояние квартиры). Поэтому важным условием успеха при применении математических методов в оценке является возможность формализовать информацию, не поддающуюся количественному измерению.

Данная проблема является общей почти для всех методов, так как не секрет, что математика оперирует числами [15].

Рассмотрим примеры перехода от качественных переменных к количественным. Самый простой случай, когда исследуемый ценообразующий фактор имеет только два качественных уровня, т.е. описывает на­личие или отсутствие какого-либо свойства (необходимость проведения текущего ремонта, наличие места для парковки). Тогда для отображе­ния в расчетных моделях данного фактора применяется бинарная пере­менная, которая при наличии признака равна 1, а при отсутствии — 0.

Если же значение признака может принимать несколько альтерна­тивных значений, которые составляют полную группу (т.е. учтены все возможные случаи), то для его отображения выбирается базовое свой­ство и объект характеризуется (n-1) бинарными переменными, каждая из которых означает наличие или отсутствие у данного объекта одного из альтернативных свойств. Если все (n-1) признака равны 0, это озна­чает, что объект обладает базовым п-м свойством. В качестве базового свойства можно выбрать то, с которым необходимо сравнить все ос­тальные свойства. Обычно в качестве базового выбирается свойство, встречающееся в выборке чаще других.

Недостатком использования бинарных переменных является то, что для кодирования каждого пункта шкалы наименований вводится от­дельная переменная. В свою очередь, введение в регрессионную модель большого числа факторных переменных потребует значительного объе­ма исходной выборки, что чаще всего представляет практически непре­одолимую проблему.

Альтернативным способом представления качественных данных является применение порядковой шкалы. При этом свойства упорядочиваются экспертным путем в порядке предпочтения. В некоторых случаях это преобразование очевидно (состояние: удовлетворительное, хорошее, очень хорошее) — свойства легко упорядочить по возрастанию (или убыванию) предпочтения, иначе необходимо прово­дить дополнительные исследования и анализ.

В практическом использовании удобна шкала качествен­ных оценок «1-9» (таблица 2), так как она позволяет учесть степень отличия.

При рассмотрении проблемы преобразо­вания качественных характеристик не существует универсального при­ема, позволяющего решить данную проблему. В качестве практических рекомендаций можно руководствоваться следующими правилами [15]:

• если позволяет объем выборки, предпочтение следует отдавать совокупности бинарных переменных;

• если объем выборки ограничен, то наиболее значимые качествен­ные характеристики следует отразить в модели с помощью бинарных переменных, а наименее значимые проранжировать с помощью шкалы "1-9".

Одним из возможных решений является построение отдельных рег­рессионных моделей для различных категорий объектов в соответствии с выбранной классификацией по качественному признаку. Например, чтобы не учитывать материал стен объектов недвижимости или количество комнат, можно разбить всю совокупность выборочных данных на несколько классов по данным признакам и построить регрессионные модели сто­имости индивидуально для каждого класса объектов.

Таблица 2

Шкала качественных оценок «1-9»

Градация оценки фактора	Значение порядковой шкалы "1-9"
Наихудшее значение фактора	1-2
Незначительное преимущество	3-4
Значительное преимущество	5-6
Явное преимущество	7-8
Абсолютное преимущество	9

2. Оценить меру зависимости каждого из отобранных факторных переменных и результирующего показателя.

Первым этапом оценки меры зависимости отобранных факторных переменных и результирующего показателя является визуальный анализ формы связи. Обязательной процедурой является построение диаграммы рассеивания, которая позволяет увидеть структуру зависимости между исследуемыми величинами. Если ваши данные содержат какие-то проблемы (например, выбросы или какие-либо неожиданные особенности), самый доступный и верный способ их обнаружить состоит как раз в анализе диаграммы рассеивания.

Для построения диаграммы рассеивания по оси абсцисс откладываются значения x, а по оси ординат – соответствующие значение y; после этого проводится визуальный анализ формы связи.

Беспорядочное расположение точек по всему полю свидетельствует об отсутствии связи между признаками (рис. 1 а). Чем сильнее связь между признаками, тем теснее будут группироваться точки вокруг определенной линии, выражающей форму связи (рис.1 б-д).

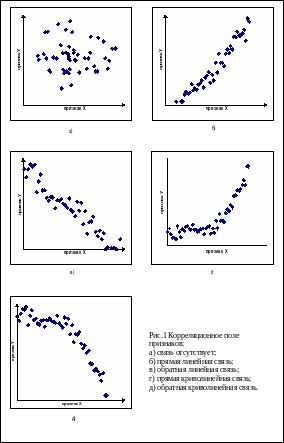
Если точки сконцентрированы вокруг линии, которая проходит из левого нижнего угла к правому верхнему (рис. 1 б, г), то связь между признаками прямая, причем в одном случае – линейная (рис. 1 б), а в другом – нелинейная (рис. 1 г). Если точки сконцентрированы вокруг линии, которая проходит от левого верхнего угла к правому нижнему углу (рис. 1 в, д), то связь между признаками обратная, причем в одном случае – линейная (рис. 1. в), в другом – нелинейная (рис. 1 д).

Более сложного анализа требуют данные в которых присутствуют нелинейные взаимосвязи. Признаком наличия нелинейной зависимости в данных является группировка точек на диаграмме рассеивания вокруг некоторой кривой (рис. 1 г, д), а не вокруг прямой линии (рис. 1 б, в). Поскольку разновидностей такого рода кривых существует достаточно много, анализ такой взаимосвязи существенно сложнее.

Необходимо заметить, что для корректного определения вида и меры связи облако точек на корреляционном поле должно быть связным, то есть не должно быть ярко выраженных отдельных точек или групп точек. Например, одна точка данных на диаграмме рассеивания, изображенной на рис. 2, представляет собой выброс.

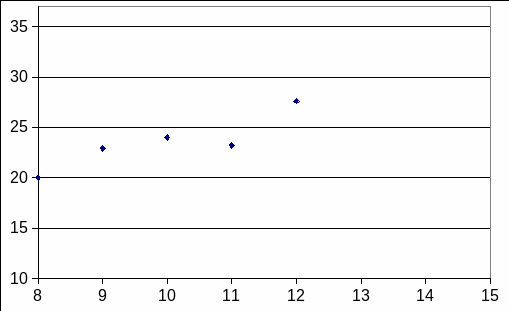
Рис. 2 Наличие выброса в данных.

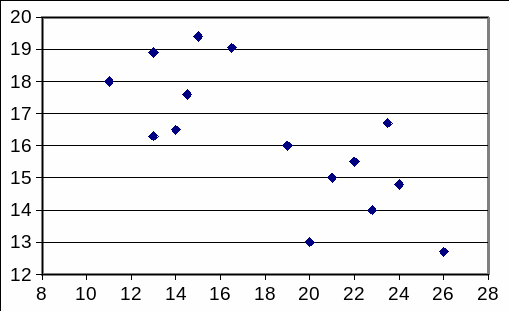
Рис. 3 Наличие двух групп в данных.

Для анализа отклонений удобно использовать графическое изобра­жение зависимости величины отклонения от расчетных значений. Если в отклонениях обнаружены выбросы (значения, далеко отстоящие от общей группы), то желательно исключить соответствующие выбросу данные из выборки и построить новую модель, не используя исключенных данных.

Анализ отклонений имеет также большое значение при выборе вида функциональной зависимости для регрессионной модели, так как распределение отклонений может указывать на математически неправильную спецификацию модели [15]. Если в расположении остатков наблюдается закономерность, это может свидетельство­вать о том, что в модели не учтен какой-то значимый фактор или же неверно подобран вид функциональной зависимости.

Особое внимание при анализе диаграмм рассеивания необходимо уделять исключению возможности корреляции вследствие неоднородности выборки. Если выборка неоднородна, то на корреляционном поле наблюдается не одно облако точек, а два или более (см. рис. 3), и тогда корреляционная зависимость будет определяться взаимным положением этих облаков, а не корреляцией внутри них.

На втором этапе оценивают количественно степень связи. В статистике не существует универсального показателя, измеряющего меру зависимости. Выбор показателя определяется видом переменных.

Пусть необходимо проанализировать степень зависимости между результирующим показателем y и факторной переменной x. В нашем распоряжении имеется выборка, содержащая n числовых пар (x_i, y_i).

Степень или теснота связи между двумя признаками измеряется рядом показателей, наиболее важным и часто применяемым из которых при линейной форме связи (рис. 1 б, в) является коэффициент корреляции, оценка которого по выборочным данным определяется по формуле:

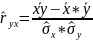(2.1)

.

Коэффициент корреляции является безразмерной величиной; его величина не зависит от выбора единиц измерения обоих признаков. Коэффициент корреляции принимает значение от –1 до 0, если связь обратная, и от 0 до +1, если связь прямая. Если значение коэффициента по абсолютной величине близко к единице, то между признаками существует тесная линейная связь; если – близко к 0, то это свидетельствует об отсутствии линейной связи между признаками, но не об отсутствии связи между ними вообще. Например, коэффициент корреляции для данных, представленных на рисунке 6 составляет всего -0,15. Ориентируясь только по этому показателю можно было бы ошибочно сделать вывод об отсутствии зависимости в данных, тогда как визуальный анализ диаграммы рассеивания позволяет наблюдать четко выраженную нелинейную зависимость. Важным моментом, который многие выпускают из вида, является тот факт, что коэффициент корреляции достаточно точно оценивает степень тесноты связи лишь в случае наличия линейной зависимости между признаками.

Для практического применения можно рекомендовать использование критериев тесноты связи, представленных в табл.2. В оценочной деятельности, когда интересующий оценщика показатель связан одновременно с большим числом различных показателей, следовательно трудно ожидать, что значения коэффициента парной корреляции будут больше 0,7.

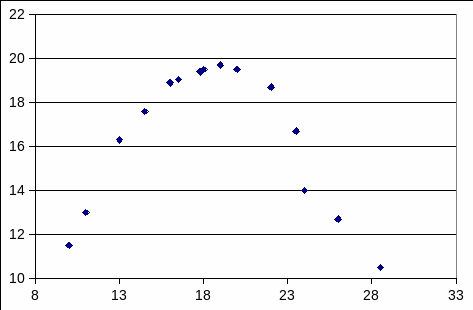
Рис. 4 Наличие нелинейной зависимости между факторами.

Таблица 3

Количественные критерии оценки тесноты связи

Абсолютная величина коэффициента корреляции	Характер связи
до 0,2	Практически отсутствует, слабая
от 0,2 до 0,3	Умеренная
от 0,3 до 0,5	Заметная
от 0,5 до 0,7	Сильная
от 0,7 до 0,99	Очень сильная

3) Провести анализ взаимосвязи между отдельными факторными переменными (проверка на наличие мультиколлинеарности).

Проверки на наличие корреляционной зависимости между факторными переменными и результирующим показателем не достаточно для принятия окончательного решения о включении данного фактора в модель, поскольку одним из условий построения модели множественной регрессии является независимость действия факторов. Ситуация, когда это условие нарушается, так называемая мультиколлинеарность, представляет собой довольно обычное явление в практике построения многофакторных регрессионных моделей [26].

4) Выбрать тип функциональной зависимости для регрессионной модели.

После того как были выявлены наиболее существенные факторы влияющие на результирующий показатель, возникает проблема подбора вида функциональной зависимости, т.е. вида многофакторной регрессионной модели. От правильности этого выбора зависит, насколько построенная модель будет адекватна изучаемому явлению, что, в свою оче­редь, предопределяет практическую ценность получаемых результатов. Недостатки плохой спецификации модели не могут быть компенсиро­ваны, например, применением более точных методов оценивания или увеличением объема выборочных данных.

Все множество видов функциональных связей делится на линейны модели и нелинейные. На практике наибольшее распространение получили линейные модели, в которых влияния различных объясняют факторов складываются:

(2.2)

где у – результирующая переменная;

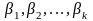– параметры (коэффициенты) уравнения множественной регрессии;

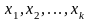– факторные переменные;

k – число факторных переменных:

u – отклонение значений результирующей переменной от истинного значения. Это ненаблюдаемая случайная величина, в ко­торой проявляется влияние на результирующую переменную других, неучтенных в модели факторов.

Линейная регрессионная модель и соответствующие ей методы оценки параметров, проверки гипотез и прогнозирования являются в целом теоретически лучше обоснованными по сравнению с нелинейным слу­чаем. Немаловажным преимуществом линейных моделей также являет­ся возможность четкой экономической интерпретации параметров мо­дели.

Однако, несмотря на все перечисленные преимущества, ограничи­ваться лишь линейными зависимостями было бы ошибкой, так как при моделировании многих процессов значительно лучшие результаты по­лучаются при использовании функций более сложного вида. В свою очередь, нелинейные модели делятся на два типа:

• линейные по параметрам (аддитивные);

• нелинейные по параметрам.

Многофакторная линейная по параметрам модель имеет вид:

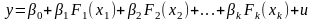, (2.3)

где F_i(x_i) могут быть различными функциями, например, 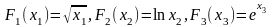, в результате замены которых переменными z_j= F_i(x_i) получаем линейную модель вида:

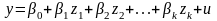. (2.4)

Все методы оценивания параметров, проверки адекватности и пост­роения прогнозов для моделей линейных по параметрам совпадают с аналогичными методами для линейных моделей.

Иначе обстоит дело с регрессией, нелинейной по оцениваемым пара­метрам. Данный класс нелинейных моделей, в свою очередь, подразде­ляется на два типа: нелинейные модели внутренне линейные и нелинейные модели внутренне нелинейные. Если нелинейная модель внутренне ли­нейна, то она с помощью соответствующих преобразований (процесс линеаризации) может быть приведена к линейному виду. В противном случае модель называется внутренне нелинейной, а этот тип моделей яв­ляется наиболее трудоемким в построении, интерпретации и примене­нии.

Например, рассмотрим так называемые мультипликативные модели, которые широко используются в практике оценки наряду с аддитивны­ми моделями. В мультипликативной модели переменные либо возво­дятся в степени, либо сами служат в качестве показателя степени, а результаты затем перемножаются. Случайная составляющая и также вхо­дит в модель мультипликативно:

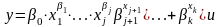(2.5)

Для оценки параметров мультипликативной модели ее необходимо преобразовать к аддитивному виду путем логарифмирования. После логарифмирования модели (2.14) получим модель линейную по пара­метрам:

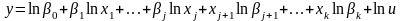. (2.6)

Для оценки параметров (коэффициентов) уравнения регрессии (2.6) с помощью метода наименьших квадратов необходимо предварительно преобразовать исходные данные наблюдений — найти логарифмы от значений результирующей переменной и той части факторных пере­менных, которые входят в модель (2.6) как аргументы логарифмичес­кой функции. При этом необходимо помнить, что логарифмированию можно подвергать переменные, которые заведомо могут принимать толь­ко положительные значения. В оценке это, например, следующие вели­чины: параметрические характеристики объектов недвижимости, вели­чина физического износа, стоимостные показатели, большинство технических характеристик оборудования. Переменные, которые могут принимать нулевые и отрицательные значения, могут входить в мульти­пликативную модель в виде показательной функции 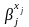. Хорошие ре­зультаты моделирования стоимости объектов недвижимости получают­ся при применении мультипликативных моделей в случае, когда в выборке цены продаж варьируются в широком диапазоне, в этом случае логарифмирование позволяет уменьшить разброс этих показателей.

Более сложный вид имеют гибридные модели, которые сочетают себе линейные и мультипликативные компоненты:

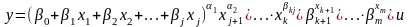(2.7)

Гибридная модель дает оценщику большую свободу при построении модели, что позволяет ему строить более качественные и содержательные модели. Однако для такого вида моделей нельзя получать статистические оценки параметров непосредственно с помощью метода наименьших квадратов. Для каждой модели приходится искать подходящий способ определения параметров.

Обычно исследователь обладает достаточной свободой при выборе функциональной формы модели. Но важно, чтобы при этом не нарушались условия, необходимые для хорошей работы применяемых методов статистического оценивания. В любом случае предпочтение следует отдавать более простым моделям, зависящим от меньшего числа параметров, так как для их статистической оценки требуется меньшее количество эмпирических данных. Также нужно проводить проверку правильности спецификации модели (прежде всего анализ отклонений) и исправлять модель, если получены неудовлетворительные результат адекватности.

Таким образом, построение регрессионной модели это многоэтапный процесс, который, как правило, требует не один раз возвращаться к этапу спецификации модели.