11

Затверджую

Завідувач кафедри № 901

кандидат технічних наук,доцент

А.І Файнер

“__” січня 2012 р.

Лекція № 4 з навчальної дисципліни

“Теорія автоматичного керування”

Тема: Елементарні ланки та їх характеристики.

Навчальний потік: 421-з.721-з,821-з.

Час 2 години. Місце згідно з розкладом занять.

Навчальні та виховні цілі:

• засвоїти поняття елементарної ланки та їх класифікацію;

• засвоїти характеристики елементарних ланок і методику їх отримання;

• виховувати у студентів освідомлення необхідності систематичного оволодіння знаннями.

Навчальні питання і розподілення часу:

Вступ………………………………………………………………………...…......5 хв.

1. Поняття елементарної ланки…...……..……………………………………...20 хв.

2. Характеристики підсилюючої, інтегруючої та диференціюючої ланок..…60 хв.

Висновки та відповіді на запитання…...……….………………..…....…………5 хв.

Навчально-матеріальне забезпечення:

1. Плакат "Таблиця перетворень".

Навчальна література:

1. Хисматулин В.Ш. Основы автоматики. – Х.: ХВУ, 1998, с. 83-93.

2. Автоматическое управление и регулирование радиотехнических систем. Часть1. Функциональные структуры и математическое описание систем автоматического управления / Д.Д. Алексейчев, А.А. Казаков. – Х.: ВИРТА ПВО, 1980, с. 94-106.

Зміст лекції та методика її викладання

Вступ.

Доведення теми лекції, її ролі у системі підготовки військового фахівця, цільової настанови та плану лекції.

Стисла характеристика літератури, що рекомендується.

1. Поняття елементарної ланки.

Передаточна функція лінійної неперервної стаціонарної САК може бути представлена у вигляді відношення многочленів відносно змінної Лапласа p:

. (1)

В силу теореми Безу многочлени і можуть бути представлені таким чином

, (2)

, (3)

де , – корені рівнянь та відповідно.

Виділимо в кожному многочлені три групи співмножників, виходячи з того, що корені рівнянь можуть бути нульовими, дійсними (відмінними від нуля) і комплексними, та перетворимо їх до деякого типового вигляду. Міркування проведемо для многочлена , що стоїть у знаменнику.

Якщо – нульовий корінь, то .

Якщо – дійсний корінь, відмінний від нуля, то відповідний співмножник можна представити у вигляді

, (4)

де

. (5)

Якщо – комплексний корінь, то завжди є комплексно спряжений корінь , і добуток відповідних їм співмножників є многочленом другого степеня, який можна представити таким чином

, (6)

де

, (7)

. (8)

Аналогічно три типи співмножників можна виділити у многочлені , що стоїть у чисельнику передаточної функції.

Припустимо, що в чисельнику і знаменнику є і нульових коренів, і дійсних відмінних від нуля коренів, і пар комплексно сполучених коренів відповідно. Тоді, як випливає з викладеного вище, передаточна функція системи може бути представлена у вигляді

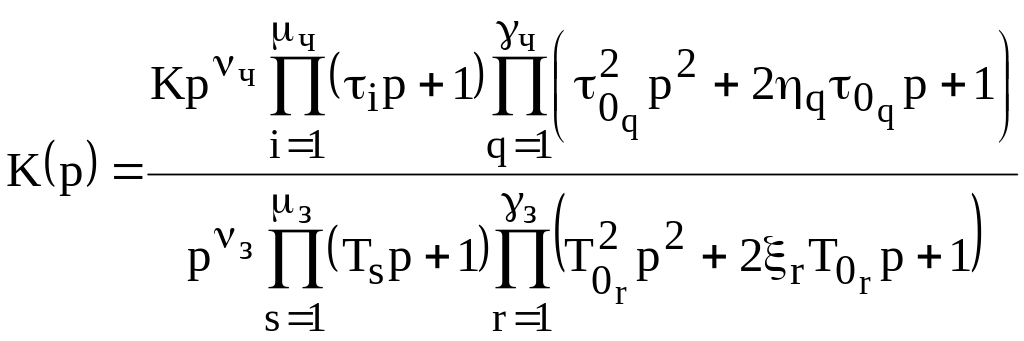, (9)

де K – числовий коефіцієнт;

,

.

Таким чином, передаточна функція лінійної неперервної стаціонарної САК може бути представлена як добуток сьомі типів співмножників: K, , , , , , .

Відзначимо, що в кожному з співмножників допускають наявність деякого чисельного множника K.

Типові співмножники передаточної функції лінійної неперервної стаціонарної САК називаються елементарними ланками. Назви елементарних ланок та їх передатні функції наведені в перших двох рядках табл. 1 – 3 на обкладинках навчального посібника. При введенні елементарних ланок вважають, що їх параметри задовольняють нерівностям , , , , , . Далі в п. 4.2 – 4.9 розглядаються основні характеристики елементарних ланок.