1.1.3. Упрощение матричных игр

Если платежная матрица игры не содержит седловой точки, то задача определения оптимальной смешанной стратегии тем сложнее, чем больше размерность матрицы. Поэтому для игр с платежными матрицами большой размерности отыскание решения можно несколько упростить, если уменьшить их размерность путем вычеркивания дублирующих и заведомо невыгодных стратегий.

Определение 1. Если в матрице игры все элементы строки (столбца) равны соответствующим элементам другой строки (столбца), то соответствующие строкам (столбцам) стратегии называются дублирующими.

Определение 2. Если в матрице игры все элементы некоторой строки, определяющей стратегию А_i игрока А, не больше (меньше или равны) соответствующих элементов другой строки, то стратегия A_i называется заведомо невыгодной.

Определение 3. Если в матрице игры все элементы некоторого столбца, определяющего стратегию В_j игрока В, не меньше (больше или равны) соответствующих элементов другого столбца, то стратегия B_j называется заведомо невыгодной.

Для того, чтобы перевести значения всех элементов платежной матрицы в область неотрицательных значений, нужно ко всем элементам матрицы добавить некоторое достаточно большое число L. При этом цена игры  увеличится на L, а решение задачи не изменится.

Таким образом, платежную матрицу можно всегда преобразовать так, что ее элементы будут целыми неотрицательными числами, а это упрощает расчеты.

Пример. Выполнить возможные упрощения платежной матрицы:

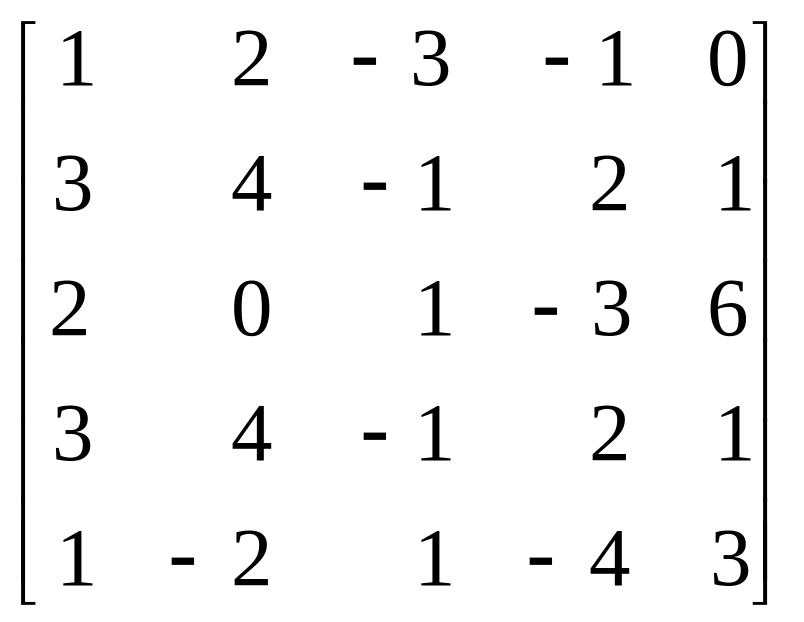. (1.1)

Решение. Поскольку соответствующие элементы второй и четвертой строк матрицы (1.1) равны, то имеет место случай с дублирующими стратегиями. Следовательно, одну из строк можно убрать (например, четвертую). Элементы первой строки меньше соответствующих элементов второй строки, а элементы пятой строки меньше или равны соответствующим элементам третьей строки. Поэтому игроку А, стремящемуся максимизировать выигрыш, выгоднее применять стратегии А₂ и А₃, а не стратегии А₁ и А₅. В связи с этим опустим первую и пятую строки, получим платежную матрицу (1.2):

. (1.2)

В преобразованной матрице (1.2) элементы первого и второго столбцов больше соответствующих элементов четвертого столбца. Поэтому игроку B, стремящемуся минимизировать проигрыш, стратегии В₁ и В₂ являются заведомо невыгодными. В связи с этим опустим первый и второй столбцы. По аналогичной причине после сравнения пятого и третьего столбцов опускаем пятый столбец. В результате приходим к матрице (1.3):

. (1.3)

Далее, для того, чтобы перевести элементы матрицы (1.3) в область неотрицательных значений добавим к каждому из них число 4. Получим матрицу (1.4):

. (1.4)

Сравнивая вновь строки полученной матрицы, заключаем, что дальнейшему упрощению она не подлежит.

1.1.4. Решение матричных игр без седловых точек

Если матрица игры содержит седловую точку, то ее решение находится по принципу минимакса (матричная игра решается в чистых стратегиях). Если же платежная матрица не имеет седловой точки, т. е.   , то решением для каждого игрока будет сложная стратегия, состоящая в случайном применении им двух и более чистых стратегий.

Если в процессе игры игрок применяет попеременно несколько чистых стратегий с определенными частотами, то такая стратегия игрока называется смешанной.

Однако, следует отметить, что применение игроками смешанных стратегий имеет смысл только тогда, когда данная игра проводится ими многократно. В случае однократно проводимой игры, не имеющей седловой точки, дать какие-либо содержательные рекомендации игрокам не представляется возможным.

Смешанной стратегией игрока А называется вектор (p₁; p₂; …, p_m), где p_i – вероятность, с которой игрок A выбирает свою чистую стратегию A_i. Компоненты вектора р удовлетворяют условиям: .

Смешанной стратегией игрока B называют вектор , где q_i – вероятность применения игроком B его чистой стратегии B_j. При этом .

Решить задачу в смешанных стратегиях означает найти такие оптимальные смешанные стратегии и , которые доставляют игроку A максимальный средний выигрыш, а игроку B – минимальный средний проигрыш.

Ценой игры  при решении в смешанных стратегиях называется величина среднего выигрыша игрока A (среднего проигрыша B), приходящегося на одну партию. Стратегии игроков, входящие в их оптимальные смешанные стратегии, называются активными.

Можно показать, что цена игры всегда удовлетворяет условию:

.

Следовательно, если каждый игрок придерживается своих смешанных стратегий при многократном повторении игры, то он получает более выгодный для себя результат, чем применяя “перестраховочные” стратегии, соответствующие  и . Каждый из игроков не заинтересован в отходе от своей оптимальной стратегии, так как ему это невыгодно.