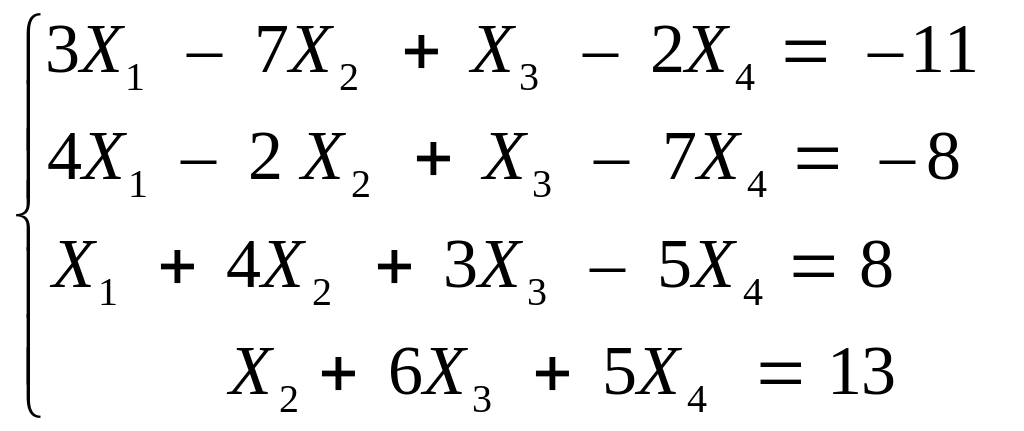Вариант |
Контрольная работа №1 Задания №. |
||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
01 |
1 |
11 |
21 |
31 |
41 |
51 |
61 |
71 |
81 |
02 |
2 |
12 |
22 |
32 |
42 |
52 |
62 |
72 |
82 |
03 |
3 |
13 |
23 |
33 |
43 |
53 |
63 |
73 |
83 |
04 |
4 |
14 |
24 |
34 |
44 |
54 |
64 |
74 |
84 |
05 |
5 |
15 |
25 |
35 |
45 |
55 |
65 |
75 |
85 |
06 |
6 |
16 |
26 |
36 |
46 |
56 |
66 |
76 |
86 |
07 |
7 |
17 |
27 |
37 |
47 |
57 |
67 |
77 |
87 |
08 |
8 |
18 |
28 |
38 |
48 |
58 |
68 |
78 |
88 |
09 |
9 |
19 |
29 |
39 |
49 |
59 |
69 |
79 |
89 |
10 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
Вариант |
Контрольная работа №2 Задания №. |
||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
01 |
91 |
101 |
111 |
121 |
131 |
141 |
151 |
161 |
171 |
02 |
92 |
102 |
112 |
122 |
132 |
142 |
152 |
162 |
172 |
03 |
93 |
103 |
113 |
123 |
133 |
143 |
153 |
163 |
173 |
04 |
94 |
104 |
114 |
124 |
134 |
144 |
154 |
164 |
174 |
05 |
95 |
105 |
115 |
125 |
135 |
145 |
155 |
165 |
175 |
06 |
96 |
106 |
116 |
126 |
136 |
146 |
156 |
166 |
176 |
07 |
97 |
107 |
117 |
127 |
137 |
147 |
157 |
167 |
177 |
08 |
98 |
108 |
118 |
128 |
138 |
148 |
158 |
168 |
178 |
09 |
99 |
109 |
119 |
129 |
139 |
149 |
159 |
169 |
179 |
10 |
100 |
110 |
120 |
130 |
140 |
150 |
160 |
170 |
180 |
Вариант |
Контрольная работа №3 Задания №. |
|||||
1 |
2 |
3 |
4 |
5 |
6 |
|
01 |
181 |
191 |
201 |
211 |
221 |
231 |
02 |
182 |
192 |
202 |
212 |
222 |
232 |
03 |
183 |
193 |
203 |
213 |
223 |
233 |
04 |
184 |
194 |
204 |
214 |
224 |
234 |
05 |
185 |
195 |
205 |
215 |
225 |
235 |
06 |
186 |
196 |
206 |
216 |
226 |
236 |
07 |
187 |
197 |
207 |
217 |
227 |
237 |
08 |
188 |
198 |
208 |
218 |
228 |
238 |
09 |
189 |
199 |
209 |
219 |
229 |
239 |
10 |
190 |
200 |
210 |
220 |
230 |
240 |
Студент должен помнить, что для приобретения опыта математического мышления и овладения избранной специальностью, для которой математические знания являются базовыми, от него требуется систематическая и упорная самостоятельная работа.
Задания на контрольные работы №1 – 3 контрольна работа №1
Для выполнения контрольной работы №1 студент должен освоить следующие темы рабочей программы:
Элементы векторной и линейной алгебры и аналитической геометрии.
Введение в математический анализ.
Дифференциальное исчисление функций одной переменной.
Применение дифференциального исчисления для исследования функций и построения их графиков.
Задача 1
1 – 10. Уровень II
Исследовать на совместность и найти общее решение системы линейных уравнений методом Гаусса: исключением неизвестных путем приведения к треугольному виду с помощью операций деления и вычитания; умножения и сложения.
1. |
|
2. |
|
|
3. |
|
4. |
|
|
5. |
|
6. |
|
|
7. |
|
8. |
|
|
9. |
|
10. |
|
|
Задача 2
11 – 20. Уровень II
Даны векторы
,
,
,
в некотором базисе. Показать, что векторы
,
,
образуют базис и найти координаты
вектора
в этом базисе. Систему линейных уравнений
решить методом Крамера.
11. |
(7,3,0), |
(4,1,1), |
(–7,1,12), |
(–1,5,10). |
12. |
(2,0,3), |
(–9,2,10), |
(–4,2,10), |
(–1, –2, –10). |
73. |
(1,2,2), |
(5, –2, –7), |
(0,5, –1), |
(–2,6, –6). |
14. |
(–2,3,1), |
(2,6,7), |
(4, –1,0), |
(6, –3, –5). |
15. |
(1,3,1), |
(1, –8,2), |
(0, –5,3), |
(3, –8,2). |
16. |
(2,5, –1), |
(–1,2, –6), |
(–2,1,1), |
(–11, –5, –1). |
17. |
(–1,4,3), |
(5,0,1), |
(–1,4,4), |
(–7,8,7). |
18. |
(3,3,2), |
(1,2,3), |
(1, –1,4), |
(4, –1,7). |
19. |
(–2, –1,1), |
(2,3,0), |
(–4,2,3), |
(–10, –9,3). |
20. |
(1,5,1), |
(–2,5,4), |
(3, –1,2), |
(4,19,9). |
Задача 3
21–30. Даны вершины А1(х1, у1, z1), А2(х2, у2, z2), А2(х3, у3, z3), А4(х4, у4, z4) пирамиды.
21. |
А1(3, –2,8), |
А2(–1,3,2), |
А3(2,0, –1), |
А4(4, –2,3). |
22. |
А1(2, –1,8), |
А2(3,4,4), |
А3(2, –1,2), |
А4(6, –1,1). |
23. |
А1(8,5,0), |
А2(–3,7, –5), |
А3(–4,1,3), |
А4(–2,1, –4). |
24. |
А1(0,1, –1), |
А2(3, –4,4), |
А3(6, –5,3), |
А4(5,2, –1). |
25. |
А1(3,2, –3), |
А2(3, –1, –1), |
А3(0,2, –2), |
А4(1, –2,3). |
26. |
А1(0,6, –1), |
А2(3,0,5), |
А3(4, –1,0), |
А4(2,1, –4). |
27. |
А1(2, –3,2), |
А2(0,5,4), |
А3(5,6,1), |
А4(–2, –2,3). |
28. |
А1(6, –2,0), |
А2(6,2, –1), |
А3(2, –1,4), |
А4(–2,7,4). |
29. |
А1(1,4, –2), |
А2(–3,0,3), |
А3(8,0,1), |
А4(1, –4,3). |
30. |
А1(1,8,2), |
А2(4, –1,2), |
А3(–1,5,3), |
А4(3,3, –3). |
Уровень I
Построить пирамиду в декартовой ортонормированной системе координат и найти:
длину ребра А1А2;
угол между ребрами А1А2 и А1А4;
уравнения высоты, опущенной из вершины А4 на грань А1А2А3.