2.2 Случайные величины и их вероятностные характеристики.

Если случайная величина ξ может принимать конечное число дискретных значений x_i, исчерпывающей вероятностной характеристикой ее служит распределение вероятностей этих значений P_i. (По аналогии со случайными функциями случайные величины обозначим буквами греческого алфавита, а их конкретные реализации – буквами латинского алфавита.)

Если случайная величина ξ непрерывна и может принимать любое значение на интервале [x_min, x_max], то ее статистической характеристикой может служить так называемый интегральный закон распределения F (x)=P(ξ<x), определяющий вероятность того, что случайная величина ξ не превзойдет значение x. Из определения интегрального закона распределения вытекает следующее очевидное соотношение:

где – вероятность того, что случайная величина ξ не выйдет за пределы интервала [x₁, x₂].

Очевидны следующие свойства функции F(x): F(x) – монотонная неубывающая функция;

Если функция F(x) дифференцируемая, то в качестве вероятностной характеристики случайной величины удобно использовать дифференциальный закон распределения или закон распределения плотности вероятности

(2.15)

Очевидны следующие соотношения:

Помимо законов распределения, часто используются числовые характеристики случайных величин, так называемые моменты распределения. Моменты, характеризующие распределение случайных величин относительно нуля, называются начальными.

Для непрерывных случайных величин начальный момент k-го порядка определяется по формуле

(2.16)

Для дискретной случайной величины ξ, принимающей значения x₁, x₂, …, x_n с вероятностями P₁, P₂, …, P_n,

(2.17)

Наиболее важное значение имеют моменты 1-го и 2-го порядков. Начальный момент 1-го порядка дает математическое ожидание или среднее значение случайной величины ξ:

(2.18)

Разность Δ_ξ=ξ – m₁(ξ) называется отклонением случайной величины. Моменты распределения отклонений случайной величины называются центральными и обозначаются M_k(ξ). Нетрудно убедиться, что M₁(ξ)=0.

Случайные величины с нулевым средним значением называются центрированными. Любые случайные величины можно свести к центрированным, если перейти к отклонениям Δ_ξ.

Начальный момент 2-го порядка определяет средний квадрат случайной величины ξ:

(2.19)

Центральный момент 2-го порядка называется дисперсией случайной величины:

(2.20)

Отношение Δ_ξ/σ_ξ называется нормированным отклонением случайной величины.

Центральный и начальный момент 2-го порядка случайной величины связаны простым соотношением:

(2.21)

Для совокупности двух случайных величин ξ₁ и ξ₂ исчерпывающей вероятностной характеристикой служит двумерный интегральный закон распределения F(x₁, x₂)=P(ξ₁<x₁, ξ₂<x₂), определяющий вероятность того, что случайные величины ξ₁ и ξ₂ не превосходят соответственно значений x₁ и x₂. Если функция F(x₁, x₂) дифференцируемая, то вероятностной характеристикой двумерной случайной величины может служить двумерный дифференциальный закон распределения или двумерная плотность вероятностей ω₂(x₁, x₂)=∂²F(x₁, x₂)/∂x₁∂x₂. Аналогично могут быть введены многомерный интегральный закон распределения и многомерные функции распределения для совокупностей из любого числа случайных величин.

Можно также ввести числовые характеристики для совокупности двух случайных величин ξ₁ и ξ₂, имеющих двумерную плотность вероятностей ω₂(x₁, x₂). Весьма важной числовой характеристикой совокупности двух случайных величин является смешанный второй центральный момент или ковариация случайных величин ξ₁ и ξ₂:

(2.22)

Если случайные величины ξ₁ и ξ₂ независимы, то ω₂(x₁, x₂)=ω(x₁)ω(x₂), и двукратный интеграл в (2.22) распадается на произведения двух однократных интегралов:

и, следовательно, M₂(ξ₁, ξ₂)=0. Поэтому ковариация M₂(ξ₁, ξ₂) может служить некоторой мерой зависимости между двумя случайными величинами. Чаще в качестве такой меры принимают безразмерный коэффициент корреляции

Две случайные величины, для которых коэффициент корреляции равен нулю, называются некоррелированными. Случайные величины, для которых 1-й начальный момент их произведения

называют ортогональными. Если средние значения случайных величин равно нулю, то понятия ортогональности и некоррелированности случайных величин совпадают.

Моменты распределения того или иного порядка, являясь важными числовыми характеристиками случайной величины, не являются, однако, их однозначной полной статистической характеристикой: случайные величины, имеющие одинаковые 1-й и 2-й моменты, могут иметь разные законы распределения.

Нормальный закон распределения.

Среди случайных величин особое место занимают нормальные случайные величины, подчиняются так называемому нормальному закону распределения:

(2.23)

Определим 1-й начальный момент нормальной случайной величины ξ:

Сделав замену , получим

так как первый из интегралов равен нулю в силу нечетности подынтегральной функции, а

Итак, a=m₁(ξ).

Определим теперь 2-й центральный момент нормальной случайной величины ξ:

так как

Таким образом, величины a и σ², полностью определяющие нормальный закон распределения, представляют собой соответственно среднее значение и дисперсию случайной величины ξ, т.е. нормальный закон распределения плотности определяется, если известны первые два момента. Из формулы (2.23) видно, что нормальное распределение симметрично относительно среднего значения случайной величины a. Максимум плотности вероятности, соответствующий x=a, равен

На рис 2.1 приведен вид нормального закона для различных σ при а=0.

Рис. 2.1

Нормальный закон распределения занимает особое положение в силу того, что большинство реальных случайных величин имеет распределение, близкое к нормальному. Последнее обстоятельство связано с тем, что на практике случайные величины обычно являются результатом совокупного действия многих независимых случайных факторов и, при некоторых условиях, по мере увеличения числа этих факторов закон распределения асимптотически приближается к нормальному. Условия эти определяются центральной предельной теоремой теории вероятности, которая в упрощенном виде может быть сформулирована следующим образом: если независимые случайные величины ξ₁, ξ₂, …, ξ_n имеют одинаковые распределения с конечной, отличной от нуля дисперсией σ², то при n→∞ сумма этих величин стремится к нормальному распределению со средним значением и дисперсией .

А. М. Ляпунов показал, что тенденция к нормализации случайных величин имеет место и при более общих предположениях.

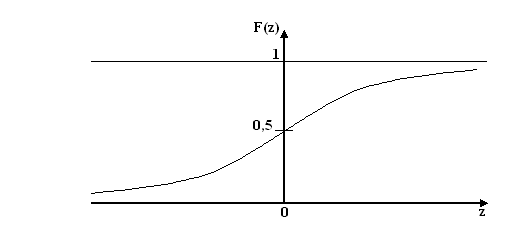
Рис. 2.2

Решение многих практических задач не столь критично к точности аппроксимации закона распределения и уже в случае, когда случайная величина определяется несколькими примерно равноценными независимыми факторами, закон ее распределения можно приближенно аппроксимировать нормальным законом.

Интегральный закон распределения, соответствующий нормальному закону (2.23), имеет вид:

(2.24)

Если перейти к нормированным отклонениям , то получим

(2.25)

Функция , представляющая собой вероятность того, что нормированное случайное отклонение не превзойдет величину z, называется интегралом вероятности. Вид этой функции приведен на рис. 2.2.

Поскольку

то F(-z)=1-F(z) и функцию F(z) достаточно определить в положительной области.

Вероятность того, что нормальная случайная величина ξ не выйдет за пределы интервала [x₁, x₂]

(2.26)