1) Максимальная скорость; 2) пропускная скорость; 3) предел скорости.

35. Пропускная способность дискретного канала без помех можно представить выражением: C_Д = V_Tlog₂m (где V_T – техническая скорость, m – объем алфавита равновероятных символов). С увеличением m, как изменяется С_Д:

1) Уменьшается; 2) увеличивается; 3) не изменяется.

36. Пропускная способность дискретного канала без помех можно представить выражением: C_Д = V_Tlog₂m (где V_T – техническая скорость, m – объем алфавита равновероятных символов). С увеличением m, как изменяется сложность технической реализации:

1) Уменьшается; 2) увеличивается; 3) не изменяется.

37. Предельная возможность канала передачи информации характеризуется коэффициентом использования канала: λ = J(z)/C_Д (где J(z) – производительность источника сообщений, С_Д – пропускная способность канала связи). Как изменяется λ:

1) λ > 1; 2) λ < 0; 3) 0 ≤ λ ≤ 1.

38. Каналы, используемые для передачи непрерывных сигналов принято называть непрерывными. Математическая модель непрерывного канала, получившая наиболее широкое распространение – это Гауссов канал. Какой дифференциальный закон распределения вероятностей (плотность вероятностей) описывает Гауссов канал:

1) равномерный; 2) нормальный; 3) экспоненциальный.

39. Пропускная способность Гауссова канала определяется, как: С_H = F_Klog₂(1+P_u/P_ζ) (где F_K – полоса пропускания, P_u/P_ζ – отношение мощности сигнала к мощности помехи). Укажите практические линии связи, обеспечивающие наибольшую С_Н:

1) двухпроводные; 2) кабельные; 3) волоконно-оптические.

40. Емкость канала передачи информации определяется, как: V_K = T_KF_KH_K (где T_K – время предоставления канала для передачи, F_K – полоса пропускания, H_K = log₂(P_u/P_ζ) – превышение мощности сигнала P_u к мощности помехи P_ζ). Какая линия связи обеспечивает наибольшую F_K:

1) двухпроводные; 2) кабельные; 3) волоконно-оптические.

41. Емкость передаваемого сигнала принято определять как: V_С = T_СF_СH_С (где T_С – длительность сигнала, F_С – ширина спектра сигнала, H_с = log₂(P_u/P_ζ) – превышение мощности сигнала P_u к мощности помехи P_ζ), а емкость канала, как V_K = T_KF_KH_K. Как следует изменить T_C, если F_C > F_K, чтобы сигнал передать по данному каналу:

1) увеличить; 2) уменьшить; 3) не изменить.

5. Основы теории кодирования.

5.1. Кодирование как процесс выражения информации в цифровой форме.

С точки зрения теории информации кодирование есть процесс сопоставления элементов алфавита источника цифрам. Правило сопоставления называется кодом. Цифры, сопоставленные элементам алфавита, называются кодовыми словами. Например, измерение аналоговой величины, выражающееся в сравнении ее с образцовыми мерами, также приводит к числовому представлению информации. Передача или хранение сообщений при этом сводится к передаче или хранению чисел. Числа можно выразить в какой-либо системе счисления. Таким образом, будет получен один из кодов, основанный на данной системе счисления.

Сравним системы счисления и построенные на их основе коды с позиций применения в системах передачи, хранения и преобразования информации.

Общепризнанным в настоящее время является позиционный принцип образования системы счисления. Значение каждого символа (цифры) зависит от его положения – позиции в ряду символов, представляющих число.

Единица каждого следующего разряда больше единицы предыдущего разряда в m раз, где m – основание системы счисления. Полное число получаем, суммируя значения по разрядам:

где i – номер разряда данного числа; – количество разрядов; a_i – множитель, принимающий любые целочисленные значения в пределах от 0 до m-1 и показывающий, сколько единиц i-го разряда содержится в числе.

Чем больше основание системы счисления, тем меньшее число разрядов требуется для представления данного числа, а следовательно, и меньшее время для его передачи.

Однако с ростом основания существенно повышаются требования к линии связи и аппаратуре создания и распознавания элементарных сигналов, соответствующих различным символам. Логические элементы вычислительных устройств в этом случае должны иметь большее число устойчивых состояний.

Учитывая оба обстоятельства, целесообразно выбирать систему, обеспечивающую минимум произведения количества различных символов m на количество разрядов l для выражения любого числа. Найдем этот минимум по графику и таблице на рис. 5.1, где показана связь между величинами m и l при воспроизведении определенного достаточно большего числа Q (Q ≈ 60000).

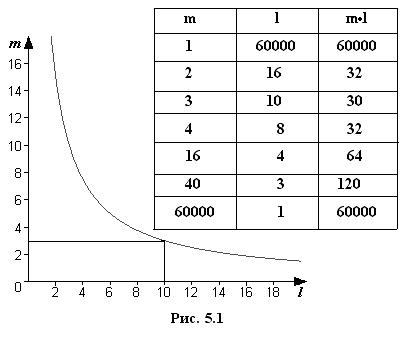
Зависимость m от l для представления числа Q = 60000.

Из графика следует, что наиболее эффективной системой является система с основанием три. Незначительно уступают ей двоичная и четверичная системы. Системы с основанием 10 и более существенно менее эффективны. Сравнивая эти системы с точки зрения удобства физической реализации соответствующих им логических элементов и простоты выполнения в них арифметических и логических действий, предпочтение необходимо отдать двоичной системе. Действительно, логические элементы, соответствующие этой системе, должны иметь всего два устойчивых состояния. Задача различения сигналов сводится в этом случае к задаче обнаружения (если импульс или нет импульса), что значительно проще.

Арифметические и логические действия также наиболее просто осуществляется в двоичной системе. В таблицы сложения, вычитания и умножения входит всего по четыре равенства:

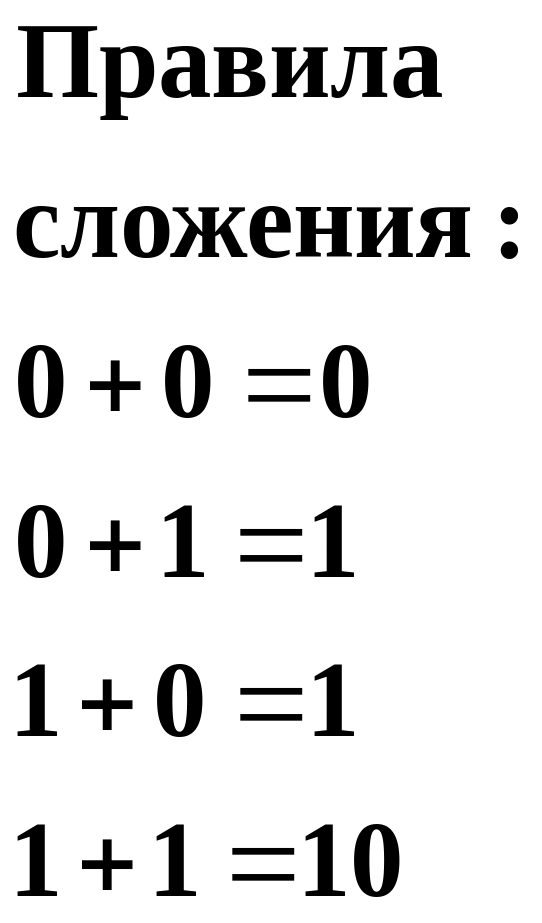
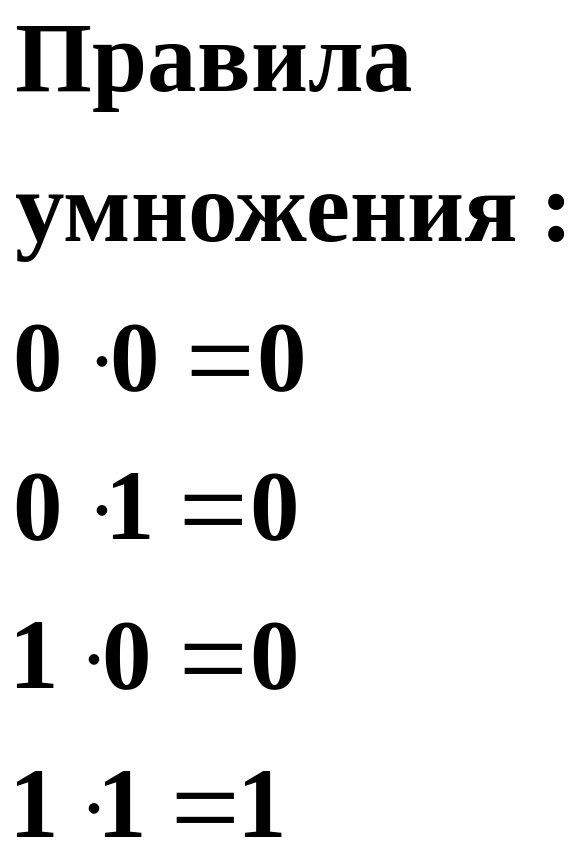
Наиболее распространенная при кодировании и декодировании логическая операция – сложение по модулю. В двоичной системе она также наиболее проста и определяется равенствами:

Алгоритм перевода из двоичной в привычную для человека десятичную систему несложен. Пересчет начинается со старшего разряда. Если в следующем разряде стоит 0, то цифра предыдущего (высшего) разряда удваивается. Если же в следующем разряде единица, то после удвоения предыдущего разряда результат увеличивается на единицу.

Пример 5.1 Найдем десятичный эквивалент двоичного числа 1001. После первой единицы слева стоит 0. Удваиваем эту единицу. Получаем число 2. Цифрой следующего младшего разряда также является 0. Удваивая число 2, получаем 4. В самом младшем разряде стоит единица. Удваивая число 4 и прибавляя 1, окончательно получаем 9.

Итак, для передачи и проведения логических и арифметических операций наиболее целесообразен двоичный код. Однако он неудобен при вводе и выводе информации, так как трудно оперировать с непривычными двоичными числами. Кроме того, запись таких чисел на бумаге оказывается слишком громоздкой. Поэтому, помимо двоичной, получили распространение системы, которые, с одной стороны, легко сводятся как к двоичной, так и к десятичной системе, а с другой стороны, дают более компактную запись. К таким системам относятся восьмеричная, шестнадцатеричная и двоично-десятичная.

В восьмеричной системе для записи всех возможных чисел используется восемь цифр от 0 до 7 включительно. Перевод чисел из восьмеричной системы в двоичную крайне прост и сводится к замене каждой восьмеричной цифры равным ей трехразрядным двоичным числом. Например, для восьмеричного числа 745 получаем:

Поскольку в восьмеричной системе числа выражаются короче, чем в двоичной, она широко используется как вспомогательная система при программировании.

Чтобы сохранить преимущества двоичной системы и удобство десятичной системы, используют двоично-десятичные коды. В таком коде каждую цифру десятичного числа записывают в виде четырехразрядного двоичного числа (тетрады). С помощью четырех разрядов можно образовать 16 различных комбинаций, из которых любые 10 могут составить двоично-десятичный код. Наиболее целесообразным является код 8-4-2-1 (табл. 5.1). Этот код относится к числу взвешенных кодов. Цифры в названии кода означают вес единиц в соответствующих двоичных разрядах. Двоично-десятичный код обычно используется как промежуточный при введении в вычислительную машину данных, представленных в десятичном коде.

В табл. 5.1 представлены два других двоично-десятичных кода с весами 5-1-2-1 и 1-4-2-1, которые широко используются при поразрядном уравновешивании в цифровых измерительных приборах.

Среди кодов, отходящих от систем счисления, большое практическое значение имеют такие, у которых при переходе от одного числа к другому изменение происходит только в одном разряде.

Таблица 5.1

Число в десятичном коде	Двоично-десятичный код с весами 8-4-2-1	Двоично-десятичный код с весами 5-1-2-1	Двоично-десятичный код с весами 2-4-2-1
0	0000 0000	0000 0000	0000 0000
1	0000 0001	0000 0001	0000 0001
2	0000 0010	0000 0010	0000 0010
3	0000 0011	0000 0011	0000 0011
4	0000 0100	0000 0111	0000 0100
5	0000 0101	0000 1000	0000 1011
6	0000 0110	0000 1001	0000 1100
7	0000 0111	0000 1010	0000 1101
8	0000 1000	0000 1011	0000 1110
9	0000 1001	0000 1111	0000 1111
10	0001 0000	0001 0000	0001 0000

Наибольшее распространение получил код Грея, часто называемый циклическим или рефлексно-двоичным. Код Грея используется в технике аналого-цифрового преобразования, где он позволяет свести к единице младшего разряда ошибку неоднозначности при считывании. Комбинации кода Грея, соответствующие десятичным числам от 0 до 15, приведены в табл. 5.2.

Правила перевода числа из кода Грея в обычный двоичный сводится к следующему: первая единица со стороны старших разрядов остается без изменения, последующие цифры (0 и 1) остаются без изменения, если число единиц, им предшествующих, четно, инвертируется, если число единиц нечетно.

Таблица 5.2

Число в десятичном коде	Код Грея	Число в десятичном коде	Код Грея	Число в десятичном коде	Код Грея
0	0000	6	0101	11	1110
1	0001	7	0100	12	1010
2	0011	8	1100	13	1011
3	0010	9	1101	14	1001
4	0110	10	1111	15	1000
5	0111

Пример 5.2. Выразим кодовое число единиц, записанное в коде Грея, в обычном двоичном коде.

Первая единица слева переписываем. Следующая цифра будет единицей, так как в этом разряде кода Грея стоит нуль и впереди только одна единица. Далее необходимо записать нуль, так как в следующем разряде исходного числа стоит единица и впереди снова имеется только одна единица. Поскольку перед последней цифрой числа в коде Грея стоят две единицы, то она должна остаться неизменной, т.е. нулем. Таким образом, число 1010 в коде Грея соответствует обычное двоичное число 1100.