Пропускная способность дискретного канала с помехами [1 и др.].
При наличии помех соответствие между множествами символов на входе и выходе канала связи перестает быть однозначным. Среднее количество информации I(S, Z), передаваемое по каналу одним символом, определяется в этом случае соотношением
(4.12)
Если статистические связи между символами отсутствуют, энтропия сигнала на выходе линии связи равна
(4.13)
При наличии статистической связи энтропию определяют с использованием цепей Маркова. Поскольку алгоритм такого определения ясен и нет необходимости усложнять изложение громоздкими формулами, ограничимся здесь только случаем отсутствия связей.
Апостериорная энтропия характеризует уменьшение количества переданной информации вследствие возникновения ошибок. Она зависит как от статистических свойств последовательностей символов, поступающих на вход канала связи, так и от совокупности переходных вероятностей, отражающих вредное действие помехи.
Если объем алфавита входных символов Z равен m1, а выходных символов S – m2, то
(4.14)
Подставив выражения (4.13) и (4.14) в (4.12) и проведя несложные преобразования, получим среднее количество информации
(4.15)
Скорость передачи информации по каналу с помехами
(4.16)
Считая скорость манипуляции VT предельно допустимой при заданных технических характеристиках канала, величину I(S,Z) можно максимизировать, изменяя статистические свойства последовательностей символов на входе канала посредством преобразователя (кодера канала). Получаемое при этом предельное значение CД скорости передачи информации по каналу называют пропускной способностью дискретного канала связи с помехами:
(4.17)
где p(z) – множества возможных распределений вероятностей входных сигналов.
Важно подчеркнуть, что при наличии помех пропускная способность канала определяет наибольшее количество информации в единицу времени, которое может быть передано со сколь угодно малой вероятностью ошибки.
Показано [6], что к пропускной способности канала связи с помехами можно приблизиться, кодируя эргодическую последовательность букв источника сообщений блоками такой длины, при которой справедлива теорема об асимптотической равновероятности длинных последовательностей.
Произвольно малая вероятность ошибки оказывается достижимой только в пределе, когда длина блоков становится бесконечной.
При удлинении кодируемых блоков возрастает сложность технической реализации кодирующих и декодирующих устройств и задержка в передаче сообщений, обусловленная необходимостью накопления требуемого числа букв в блоке. В рамках допустимых усложнений на практике при кодировании могут преследоваться две цели: либо при заданной скорости передачи информации стремятся обеспечить минимальную ошибку, либо при заданной достоверности – скорости передачи, приближающуюся к пропускной способности канала.
Предельные возможности канала никогда не используются полностью. Степень его загрузки характеризуется коэффициентом использования канала
,
(4.18)
где Ru(Z) – производительность источника сообщений; СД – пропускная способность канала связи.
Поскольку нормальное функционирование канала возможно, как показано далее, при изменении производительности источника в пределах 0≤ Ru(Z)≤ СД, λ теоретически может изменятся в пределах от 0 до 1.
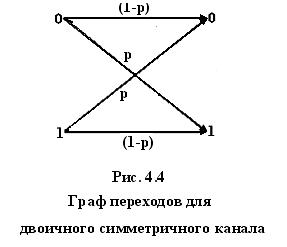
Пример 4.4 Определить пропускную способность двоичного симметричного канала (ДСК) со скоростью манипуляции VT в предположении независимости передаваемых символов.
Запишем соотношение (4.14) в следующем виде:
Воспользовавшись обозначениями на графе (рис. 4.4), можем записать
Так как p(0) + p(1) =1, то
Величина H(Z|S) не зависит от вероятностей входных символов, что является следствием симметрии канала.
Следовательно, пропускная способность
Максимум H(Z) достигается при равенстве вероятностей появления символов, он равен 1. Отсюда
(4.19)
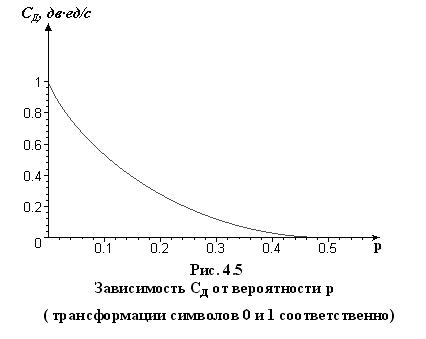
График зависимости пропускной способности ДСК от p показан на рис. 4.5. При увеличении вероятности трансформации символа с 0 до ½ СД(p) уменьшится от 1 до 0. Если p=0, то шум в канале отсутствует и его пропускная способность равна 1. При p=1/2 канал бесполезен, так как значения символов на приемной стороне с равным успехом можно устанавливать по результатам подбрасывания монеты (герб – 1, решетка – 0). Пропускная способность канала при этом равна нулю.
