2. Скорость передачи информации по дискретному каналу [1 и др.].

Характеризуя дискретный канал связи, используют два понятия скорости передачи: технической и информационной.

Под технической скорости передачи V_T, называемой также скоростью манипуляции, подразумевают число элементарных сигналов (символов), передаваемых по каналу в единицу времени. Она зависит от свойств линии связи и быстродействия аппаратуры канала.

С учетом возможных различий в длительностях символов скорость

(4.8)

где τ_ср – среднее значение длительности символа.

При одинаковой продолжительности τ всех передаваемых символов τ_ср=τ.

Единицей измерения технической скорости служит бод – скорость, при которой за одну секунду передается один символ.

Информационная скорость или скорость передачи информации, определяется средним количеством информации, которое передается по каналу в единицу времени. Она зависит как от характеристик данного канала связи, таких, как объем алфавита используемых символов, техническая скорость их передачи, статистические свойства помех в линии, так и от вероятностей поступающих на вход символов и их статистической взаимосвязи.

Если по каналу передается z_k символов в единицу времени, т.е. техническая скорость равна V_T, а среднее количество информации на один символ канала равно J(Z, S), то скорость передачи информации по каналу R_k задается соотношением

(4.9)

где J(Z, S) – среднее количество информации, переносимое одним символом.

2. Пропускная способность дискретного канала без помех [1 и др.].

Для теории и практики важно выяснить, до какого предела и каким путем можно повысить скорость передачи информации по конкретному каналу связи. Предельные возможности канала по передаче информации характеризуется его пропускной способностью.

Пропускная способность канала С_д равна той максимальной скорости передачи информации по данному каналу, которой можно достигнуть при самых совершенных способах передачи и приема:

(4.10)

При заданном алфавите символов и фиксированных характеристиках канала (например, полосе частот, средней и пиковой мощности передатчика) остальные характеристики должны быть выбраны такими, чтобы обеспечить наибольшую скорость передачи по нему элементарных сигналов, т.е. обеспечить максимальное значение V_T. Максимум среднего количества информации, приходящейся на один символ принятого сигнала I(Z, S), определяется на множестве распределений между символами S₁, …, S_i, …, S_m.

Пропускная способность канала, как и скорость передачи информации по каналу, измеряется числом двоичных единиц информации в секунду (дв. ед./с. или бит./с.).

Так как в отсутствии помех имеет место взаимно-однозначное соответствия между множеством символов {z} на выходе канала и {s} на его входе, то I(Z, S)=I(S, Z)=H(S). Максимум возможного количества информации на символ равен logm, где m – объем алфавита символов, откуда пропускная способность дискретного канала без помех

(4.11)

Следовательно, для увеличения скорости передачи информации по дискретному каналу без помех и приближения ее к пропускной способности канала последовательность букв сообщения должна подвергнутся такому преобразованию в кодере, при котором различные символы в его выходной последовательности появлялись бы по возможности равновероятно, а статистические связи между ними отсутствовали бы.

Доказано (см [9], §5.4), что это выполнимо для любой эргодической последовательности букв, если кодирование осуществлять блоками такой длины, при которой справедлива теорема об их асимптотической равновероятности.

Расширение объема алфавита символов m приводит к повышению пропускной способности канала (рис. 4.3.), однако возрастает и сложность технической реализации.

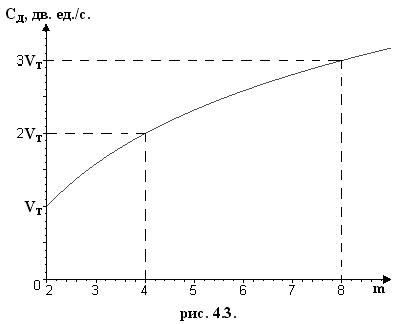
График изменения С_Д=φ(m), где m – объем алфавита символов передачи.