2. Энтропия непрерывного источника информации (дифференциальная энтропия) [1, 2 и др.].

В предыдущих параграфах была рассмотрена мера неопределенности выбора для дискретного источника информации. На практике мы в основном встречаемся с источниками информации, множество возможных состояний которых составляет континуум. Такие источники называют непрерывными источниками информации.

Во многих случаях они преобразуются в дискретные посредством использования устройств дискретизации и квантования. Вместе с тем существует немало и таких систем, в которых информация передается и преобразуется непосредственно в форме непрерывных сигналов. Примерами могут служить системы телефонной связи и телевидения.

Оценка неопределенности выбора для непрерывного источника информации имеет определенную специфику. Во-первых, значения, реализуемые источником, математические отображаются непрерывной случайной величиной. Во-вторых, вероятности значений этой случайной величины не могут использоваться для оценки неопределенности, поскольку в данном случае вероятность любого конкретного значения равна нулю.

Естественно, однако, связывать неопределенность выбора значения непрерывной случайной величины с плотностью распределения вероятностей этих значений, относящихся к любому сколь угодно малому интервалу непрерывной случайной величины, вероятность конечна, попытаемся найти формулу для энтропии непрерывного источника информации, используя операции квантования и последовательного перехода при уменьшении кванта до нуля

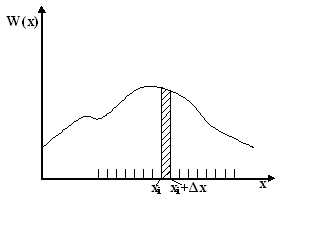
Рис. 3.3

С этой целью разобьем диапазон изменения непрерывной величины X характеризующейся плотностью распределения вероятностей W(x), на конечное число n малых интервалов шириной Δx (рис. 3.3). При реализации любого значения x, принадлежащего интервалу (x_i, x_i+Δx), будем считать, что реализовалось значение x_i дискретной случайной величины X. Поскольку Δx мало, вероятность p(x_i≤x≤x_i+Δx) реализации значения x из интервала (x_i, x_i+Δx):

Тогда в соответствии с (3.5) информация на один отсчет такого квантованного сигнала равна (отсчеты полагаем некоррелированными):

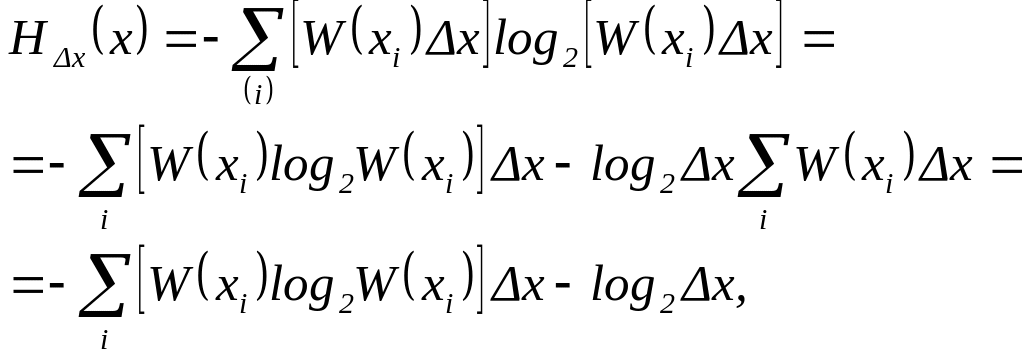
так как

Переходя к пределу при Δx→0, получаем, что энтропия на один отсчет непрерывного источника сообщений равна

(3.19)

Первый член правой части (3.19)

(3.20)

называется дифференциальной энтропией непрерывного распределения (источника непрерывного сообщения). Величина h(x) имеет конечное значение. Она не зависти от шага квантования Δx, а зависит только от закона распределения непрерывной величины x. Второй член правой части (3.19), напротив, не зависит от характеристик источника сообщений, а определяется только шагом квантования Δx уровня сигнала. Можно легко проследить влияние его на энтропию сигнала: при увеличении или уменьшении величины Δx энтропия соответственно монотонно убывает или возрастает.

Свойства дифференциальной энтропии.

1. Дифференциальная энтропия в отличии от энтропии дискретного источника является относительной мерой неопределенности. Ее значение зависит от масштаба случайной величины X, а следовательно, и от выбора ее измерения.

Изменим масштаб случайной величины X, например, в k раз, оставив неизменным масштаб равномерно распределенной в единичном интервале случайной величины X, принятой за эталон. Если x_k=kx, то W(x_k)=W(x)/k.

Тогда

(3.21)

Если одновременно изменить масштаб величины X, то относительная неопределенность также изменится, так как значение эталона будет уже иным.

Из относительности дифференциальной энтропии следует, что энтропия может принимать положительные, отрицательные и нулевые значения.

2. Дифференциальная энтропия не зависит от конкретных значений случайной величины X и, в частности, от изменения всех ее значений на постоянное. Действительно, масштаб X при этом не меняется и справедливо равенство

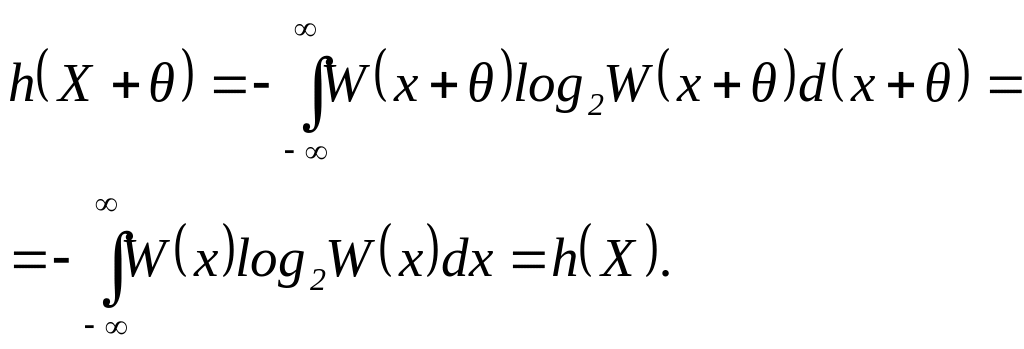(3.22)

3. Какие же непрерывные распределения обладают максимальной дифференциальной энтропией?

а) Если единственным ограничением для случайной величины X является область ее возможных значений [α, β], то максимальной дифференциальной энтропией обладает равномерное распределение вероятностей в этой области.

При доказательстве решается задача определения плотности распределения W(x), обеспечивающей максимальное значение функционала

при ограничении

Используя, например, метод неопределенных множителей Лагранжа. получим

(3.23)

Нетрудно убедится в том, что найденная функция W(x) обеспечивает максимум функционала h(X), причем

(3.24)

б) Если ограничения на область значений непрерывной случайной величины X отсутствуют, но известно, что дисперсия ее ограничена, то максимальной дифференциальной энтропией обладает нормальное распределение величины X.

При доказательстве решается задача определения функции W(x), обеспечивающей максимальное значение функционала

(3.25)

при ограничениях

и

где σ – среднеквадратическое отклонение от математического ожидания (σ – заданное ограничение).

Искомую плотность распределения W(x) находят, например, методом неопределенных множителей Лагранжа.

Она оказывается гауссовской:

(3.26)

Вычислив функционал (3.25) для этого распределения, получим значение максимальной дифференциальной энтропии h_max(X). В двоичных единицах неопределенности

(3.27)

Поскольку в информационных системах сигнала, описываемый случайной величиной X, часто представляет собой электрическое напряжение (или ток), дисперсия X пропорциональна средней мощности сигнала. Тогда в соответствии с (3.26) можно утверждать, что при заданной мощности наибольшей средней неопределенностью выбора будет обладать источник, генерирующий сигналы, амплитуды которых распределены по нормальному закону.

4. Соотношения для дифференциальной энтропии объединения статистически зависимых непрерывных источников аналогичны соответствующим формулам для дискретных источников:

(3.28)

где

Пример 3.4 Определить, насколько мы выиграем в мощности, используя для организации мешающего воздействия, характеризующегося энтропией, источник шума с гауссовской плотностью распределения по сравнению с источником, имеющим в интервале [α, β] равномерную плотность распределения.

В соответствии с (3.27) дифференциальная энтропия гауссовского распределения

где σ_г² – дисперсия, характеризующая мощность, выделяемую на резисторе с сопротивлением в 1Ом.

Для равномерного распределения энтропия определена соотношением (3.24):

Вычислим дисперсию σ_р² равномерного на интервале [α, β] распределения:

(3.29)

Из условия обеспечения равенства энтропий следует

(3.30)

(3.31)

Возведя (3.31) в квадрат и подставив в (3.29) получим

Следовательно, искомый выигрыш составляет 42%.