2. Условная энтропия и ее свойства [1,2 и др.].

При оценке меры неопределенности выбора исхода опыта часто необходимо учитывать статистические связи, которые в большинстве случаев имеют место как между состояниями двух или нескольких источников, объединенных в рамках одной системы, так и между состояниями, последовательно выбираемыми одним источником.

Определим энтропию объединения двух статистически связанных ансамблей X и Y. Объединение ансамблей характеризуется матрицей p(X,Y) вероятностей p(x_i, y_j) всех возможных комбинаций состояний x_i(1≤i≤N) ансамбля X и состояний y_j(1≤j≤k) ансамбля Y:

(3.12)

Суммируя столбы и строки матрицы (3.12), получим информацию об ансамблях X и Y исходных источников x и y:

При известных вероятностях p(x_i, y_j) появления пары (x_i, y_j) энтропия системы сигналов X, Y в соответствии с формулой (3.9) определяется выражением

(3.13)

Проанализируем это выражение. Согласно теореме умножения вероятностей,

(3.14)

(3.15)

Здесь p(y_j) и p(x_i) – вероятности появления элементов соответственно и ; p(y_j|x_i) – условная вероятность появления элемента при условии, что уже известен элемент ; p(x_i|y_j) – условная вероятность появления элемента при условии, что уже известен элемент .

Подставив в формулу (3.13) и (3.14), получим

Учитывая, что log p(y_j)p(x_i|y_j)=log p(y_j)+log p(x_i|y_j), последнее выражение перепишем в виде

Имея в виду, что , получим

Рассмотрим сумму . Согласно формуле (3.5) эта сумма представляет собой энтропию сигнала Y. Сумма представляет собой случайную величину, характеризующую неопределенность, приходящуюся на одно состояние ансамбля Y при условии, реализовалась конкретное состояние x_i ансамбля X. Эта условная энтропия относительно элемента y_j называется частной условной энтропией. Обозначим ее через H(X|y_j). В результате получим

Сумма представляет собой усредненное значение частной условной энтропии H(X|y_j) по всем возможным значениям сигнала Y и называется условной энтропией сигнала X относительно сигнала Y. Обозначив условную энтропию через H(X|Y), получим

(3.16)

Если в равенство (3.13) подставить выражение (3.15), а не (3.14), то после аналогичных преобразований получим

(3.17)

Формулы (3.16) и (3.17) позволяет сделать вывод, что энтропия объединения двух сигналов X и Y равна энтропии одного из этих сигналов плюс условная энтропия второго сигнала относительно первого.

Свойства условной энтропии

Покажем, в каких пределах может изменятся энтропия объединения двух сигналов: X и Y. Выражение для условной энтропии в развернутой форме имеет вид

(3.18)

Известно, что для независимых случайных событий условные вероятности равны безусловным. Предположив, что составляющие X и Y сигнала (X, Y) независимы, тогда в формуле (3.18) возможна замена p(x_i|y_j)=p(x_i) и она может быть преобразована к виду

Учитывая, что , имеем

Таким образом, условная энтропия при независимых сигналах равна безусловной энтропии, и в этом случае формулы (3.16) и №.17) примут одинаковый вид: H(X, Y)=H(X)+H(Y).

Рассмотрим теперь другой крайний случай, когда сигналы X и Y полностью зависимы, т.е. если получена конкретная реализация сигнала X, то тем самым известна и реализация сигнала Y.

Пусть сигнал X принял значение x_k. При этом известно, что сигнал Y с необходимостью примет значение y_s. Это значит, что условная вероятность p(y_s|x_k)=1, все остальные условные вероятности p(y_j|x_i), (j, i)≠(s, k), примут нулевое значение. Тогда в формулу (3.18) будут входить слагаемые двух видов: либо p(x_i)∙1∙log1, либо p(x_i)∙0∙log0. И в этом и в другом случае эти слагаемые равны нулю, поэтому H(Y|X)=0.

Рассуждая аналогично, можно показать, что при полностью зависимых сигналах X и Y энтропия H(X|Y)=0.

Таким образом, в случае полной зависимости сигналов X и Y энтропия их объединения равна энтропии одного из этих сигналов H(X, Y)=H(X)=H(Y), т. е. каждый сигнал содержит всю информацию относительно другого сигнала.

Уяснению соотношений между рассмотренными энтропиями дискретных источников информации (ансамблей) способствует их графическое отображение (рис. 3.2).

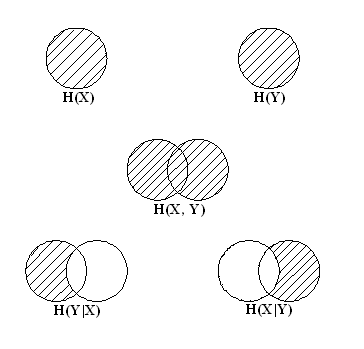
Рис. 3.2

Условное графическое представление H(X), H(Y), H(X, Y), H(Y|X) и H(X|Y).

Пример 3.3. Определить энтропию H(X), H(Y), H(X|Y), H(X, Y), если задана матрица вероятностей состояний системы, объединяющей источники x и y:

Вычисляем безусловные вероятности состояний каждой системы как суммы совместных вероятностей по строкам и столбцам заданной матрицы:

Определяем условные вероятности

Проверим результат по формуле