2. Свойства энтропии [1,3 и др.].

Рассмотрим основные свойства энтропии, обратив внимание на то, что сформулированные условия для меры неопределенности выполняются.

1. Энтропия является вещественной и неотрицательной величиной, так как для любого i(1≤i≤N) p_i изменяется в интервале от 0 до 1, log(p_i) отрицателен и, следовательно, -p_ilog(p_i) положительна.

2. Энтропия – величина ограниченная. Для слагаемых –p_ilog(p_i) в диапазоне 0<p_i≤1 ограниченность очевидна. Остается определить предел, к которому стремится слагаемое –p_ilog(p_i) при p_i→0, поскольку -log(p_i) при этом неограниченно возрастает:

Обозначив и воспользовавшись правилом Лопиталя, получим

3. Энтропия обращается в нуль лишь в том случае, если вероятность одного из состояний равна единице; тогда вероятности всех остальных состояний, естественно, равны нулю. Это положение соответствует случаю, когда состояние источника полностью определено.

4. Энтропия максимальна, когда все состояния источника равновероятны, что легко доказывается методом неопределенных множителей Лагранжа:

(3.7)

5. Энтропия источника x с двумя состояниями x₁ и x₂ изменяется от нуля до единицы, достигая максимума при равенстве их вероятностей:

График зависимости H(X) в функции p

(3.8)

приведены на рис. 3.1

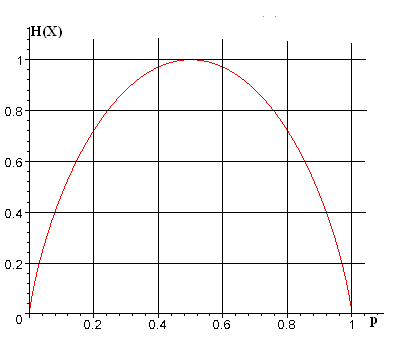
Рис. 3.1. Зависимость энтропии H(X) от вероятности p.

При p<<(1-p) частная неопределенность, приходящаяся на состояние x₁ велика, однако такие состояния источника весьма редки. Состояния x₂ реализуются часто, но неопределенность, приходящаяся на такое состояние, очень мала. Поэтому энтропия, характеризующая среднюю неопределенность на одно состояние ансамбля , так же мала. Аналогичная ситуация наблюдается при p>>(1-p).

Отметим, что энтропия непрерывно зависит от вероятностей отдельных состояний, что непосредственно вытекает из непрерывности функции –plogp.

6. Энтропия объединения нескольких статистически независимых источников информации равна сумме энтропий исходных источников.

Не теряя общности, ограничимся рассмотрением объединения, включающего два источника информации x и y понимают обобщенный источник информации (x, y), характеризующийся вероятностями p(x_i, y_j) всех возможных комбинаций состояний x_i источника X и y_j источника Y. Аналогично трактуется и объединение ансамблей.

В соответствии с определением энтропия объединения

(3.9)

здесь p(x_i, y_j) – вероятности совместной реализации состояний

и

В случае статистической независимости источников информации x и y запишем

тогда

Учитывая, что

и

получим

(3.10)

Соответственно для энтропии объединения нескольких независимых источников x,y,z имеем

(3.11)

В дальнейшем для придания общности получаемым результатам о неопределенности выбора будем говорить в основном применительно к математическим моделям источников информации в виде ансамблей.

7. Энтропия характеризует среднюю неопределенность выбора одного состояния из ансамбля. При ее определении используют только вероятности состояний, полностью игнорируя их содержательную сторону.

8. Энтропия как мера неопределенности согласуется с экспериментальными данными, полученными при изучении психологических реакций человека, в частности реакции выбора. Установлено, что время безошибочной реакции на последовательность беспорядочно чередующихся равновероятных раздражителей (например, загорающихся лампочек) растет с увеличением их числа так же, как энтропия. Это характеризует неопределенность выбора одного раздражителя.

Замена равновероятных раздражителей неравновероятными приводит к снижению среднего времени реакции ровно настолько, насколько уменьшается энтропия.