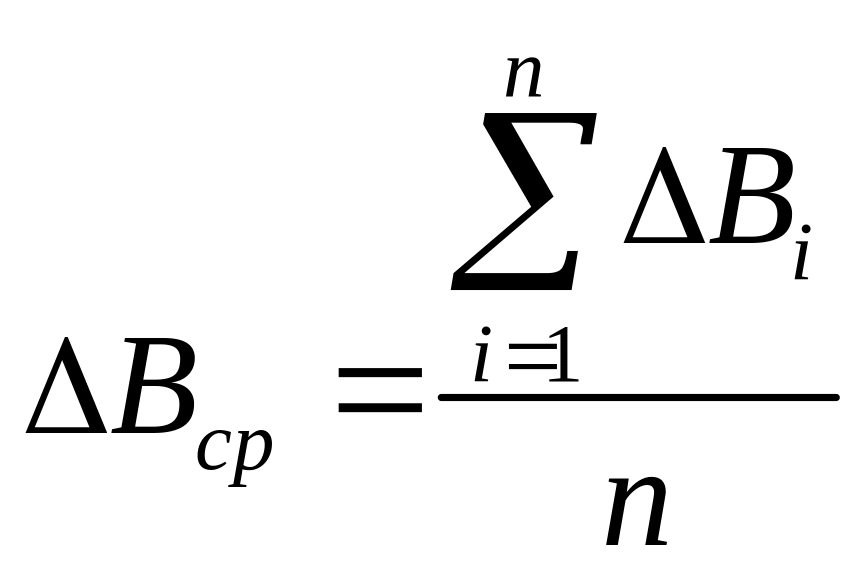Вычисление погрешностей при косвенных измерениях

Очень редко содержание экспериментальной работы сводится к получению результата прямого измерения. Большей частью искомая величина В является функцией нескольких других неизвестных величин x , y , z , которые измеряются непосредственно. Таким образом, величина B является косвенно измеряемой величиной. Ее погрешность определяется погрешностью величин, непосредственно измеряемых.

Для расчета погрешностей косвенно измеряемой величины используется аппарат дифференциального исчисления. При этом считается, что погрешность измерения много меньше самих измеряемых величин , , и т.д., следовательно, знаки приращения () можно заменить на знаки дифференциала (d). Если величина В является функцией величин x, y , z , то полный дифференциал функции выражается

Поэтому абсолютная погрешность В косвенно измеряемой величины В будет

,

где , , – модули частых производных функции по x , y, z;

 x , y,  z – предельные абсолютные погрешности непосредственно измеряемых величин x , y , z .

Относительная погрешность косвенно измеряемой величины В

Значение В_ср вычисляется по формуле .

Результат записывается в виде

Пусть, например,

Находим полный дифференциал dB

Абсолютная погрешность будет

Относительная погрешность косвенно определяемой величины

Ниже приводится табл. 2 формул для вычисления погрешности с использованием указанных выше правил для величины В, представленной простейшими функциональными зависимостями.

Таблица 2

№ п/п	В	В
1	2	3	4
1
2
3
4
5
6
1	2	3	4
7
8
9
10

Порядок обработки результатов прямых и косвенных измерений приведен в табл. 3 и 4.

Таблица 3

Обработка результатов прямых измерений физической величины

№ п/п	Порядок вычисления	Формула
1	2	3
1	Получены n измерений величины a	а1 , а2 . . . аn
2	Приборная погрешность	априб
3	Среднее арифметическое аср из всех измерений
1	2	3
4	Абсолютная погрешность отдельных измерений аi
5	Средняя абсолютная погрешность отдельных измерений аср
6	Предельная абсолютная погрешность результата апред а) если , то б) если , то предельная погрешность
7	После округления результат измерения записывается в виде
8	Предельная относительная погрешность

Таблица 4

Обработка результатов косвенных измерений величины

№ п/п	Порядок вычисления		Формула
1	2		3
1. При однократном измерении величины В
1	Получены прямые измерения величин Они записаны в виде			x , y , z
2	Вычисляется среднее значение окончательного результата одного измерения Вср
3	Вычисляется предельная абсолютная погрешность
1	2			3
4	Вычисляется предельная относительная погрешность
5	Окончательный результат записывается в виде
2. При проведении многократных измерений величины
6		Получены n косвенных измерений
7		Вычисляется среднее арифметическое значение Вср из результатов отдельных косвенных измерений
8		Вычисляются абсолютные погрешности отдельных косвенных измерений
9		Средняя абсолютная погрешность результатов
10		После округления Вср и Вср окончательный результат запишется в виде

В окончательном результате, как и в любых численных обозначениях, необходимо поставить единицы измерения, т.к. без этого численный результат измерений в физике не имеет смысла, равно как отсутствие вычисленных погрешностей лишает его всякой ценности.

Рассмотрим пример расчета результата измерений при выполнении лабораторной работы.

Требуется определить объем полого цилиндра, расчетная формула которого

,

где D – внешний диаметр;

d – внутренний диаметр;

h – высота цилиндра.

D, d, h – непосредственно измеряемые величины.

Объем V измеряется косвенно, диаметры D и d измеряются штангецир-кулем, цена деления которого 0,1 мм , т.е. D_приб = d_приб = 0,1 мм . Высота измеряется микрометром, приборная погрешность которого h_приб = 0,01 мм.

Пусть результат непосредственного измерения запишется следующим образом:

h = ( 18,13  0,02 ) мм ,

D = ( 43,3  0,1 ) мм ,

d = ( 24,5  0,1 ) мм.

Рассчитаем объем V_ср

мм³

Рассчитаем относительную погрешность _v по формуле, полученной в результате применения правил вычисления погрешностей

Входящие в формулу погрешности уже вычислены. Погрешность  может быть сделана сколько угодно малой, если взять  с достаточным количеством знаков. Возьмем  = 3,14 , тогда  = 0,002 (т.к.  = 3,14159…) . Подставляя погрешность получим

Абсолютная погрешность результата

мм³

Окончательный результат измерений

V = ( 181  2)  10² мм³

Лабораторная работа 1