3.4 2.Бинарная фазовая манипуляция

Для двухуровневой фазовой модуляции (М = 2) модулирующий сигнал может принимать два различных значения, определяемые передаваемым символом в исходной бинарной информационной последовательности. Другими словами, передаваемым информационным символам 0 или 1 соответствуют два возможных значения фазы колебания несущей частоты при выполнении условия

. (1)

Конкретные значение фазовых состояний, очевидно, не имеют значения, важно лишь расстояние между ними, равное . Без ограничения общности можно предположить, что значения модулирующего сигнала равны 0 и , как это определено в (1) . В более общем виде колебание с фазовой модуляцией можно представить в виде

(2)

где – фазовые состояния несущей, k = 1, 2, …, M; q(t) – форма импульса в модулирующем сигнале, ω_с – несущая частота, А – постоянная амплитуда.

Дифференциальная фазовая манипуляция

Многолучевое распространение проявляется в конструктивной и деструктивной интерференции и может сопровождаться дополнительными быстрыми поворотами фазы несущего колебания. За время отсчета символа накапливаются фазовые смещения фазового угла несущей частоты, что приводит к ошибочному приему символа. Ошибка, накопленная в одном символе, аккумулируется с ошибками, возникающими при выделении последующих символов. В качестве противодействия этому процессу используют кодирование, простейшим вариантом которого является дифференциальное фазовое кодирование. При этом информация, содержащаяся в модулированном сигнале, сохраняется в изменениях (differences) относительной фазы лучше, чем в изменениях абсолютных величин фазы.

Принципиальное отсутствие несущей частоты в спектре модулированного сигнала в некоторых случаях приводит к неоправданному усложнению демодулятора приемника. QPSK и BPSK сигналы могут быть приняты только когерентным детектором, для реализации которого необходимо либо передавать наравне с сигналом еще и опорную частоту или реализовывать в приемнике специальную схему восстановления несущей. Очевидно, что для недорогой аппаратуры удобнее было бы использование значительно более простого детектора огибающей.

П рименение детектора огибающей для фазоманипулированных колебаний возможно в том случае, когда эта модуляция реализуется в дифференциальном виде (DPSK). Схема демодулятора сигнала с QPSK показана на рис. 4.4

В системах передачи бинарных цифровых сигналов для реализации дифференциальной модуляции исходный цифровой модулирующий сигнал, прежде чем поступить на модулятор, кодируется по следующему алгоритму:

, (4)

где m_k – иcходная бинарная последовательность, d_k – результирующая бинарная последовательность, – символ сложения по модулю два.

В передатчике дифференциальное кодирование реализуется в схеме задержки сигнала на временной интервал, равный длительности одного бита информации и несложной логической схемы (рис. 4.5). Пример дифференциального кодирования показан в табл. 4.2.

Таблица 4.2 Дифференциальное кодирование бинарного цифрового сигнала

		1	0	0	1	0	1	1	0
		1	1	0	1	1	0	0	0
	1	1	0	1	1	0	0	0	1

И дея дифференциального кодирования состоит в том, что передается не абсолютное значение информационного символа, а его изменение (или не изменение) относительно предыдущего значения, т.е. каждый последующий передаваемый символ содержит в себе информацию о предыдущем символе. Тем самым для извлечения исходной информации в качестве опорного сигнала можно использовать не несущую частоту, а предыдущее значение символа. В самом деле, если в приемнике (рис. 4.6) осуществить задержку принятого символа на один символьный интервал, а затем произвести перемножение полученного и задержанного символов, то результатом этой операции будет исходная информационная последовательность:

. (5)

После фильтрации с помощью ФНЧ или согласованного фильтра в (5) остается только постоянная составляющая и, с учетом (4), получим:

. (6)

Очевидно, что ни временная форма, ни спектральный состав дифференциального DВPSK сигнала не будет отличаться от обычного BPSK сигнала.

Пример 4.2. Рассмотрим один из важных компонентов системы спутниковой радионавигации – метод дифференциальной фазовой манипуляции, используемый в системе ГЛОНАСС. Этот метод реализуется посредством перекодировки исходной последовательности информационных символов по алгоритму (4). При приеме перекодировка выполняется по алгоритму (6).

Изучение метода дифференциальной фазовой манипуляции проведем в среде систем SIMULINK и MatLAB.

Из блоков библиотеки SIMULINK соберем схему, представленную на рис. 4.6. В этой схеме используются следующие блоки: блок Repeating Sequence Interpolated содержит данные (символы), которые надлежит перекодировать, чтобы получить последовательность символов с дифференциальной фазовой манипуляцией. Блоки Unit Delay выполняют задержку на один символ, блоки Logical Operator XOR – это сумматоры по модулю два. Блок Scope – представляет собой трехканальный осциллограф, регистрирующий результаты работы схемы.

Символы [1101010100] в сигнальной форме представлены на верхнем графике рис. 4.7 и соответствуют данным, передаваемым по соответствующему каналу (рис. 4.6). Средний график рис. 4.7 – это результат выполнения алгоритма (6) и соответствует данным, сформированным в другом канале рис. 4.4. Нижний график рис. 4.7 представляет собой результат применения алгоритма (6) восстановления данных и соответствует данным, сформированным в нижнем канале рис. 4.6.

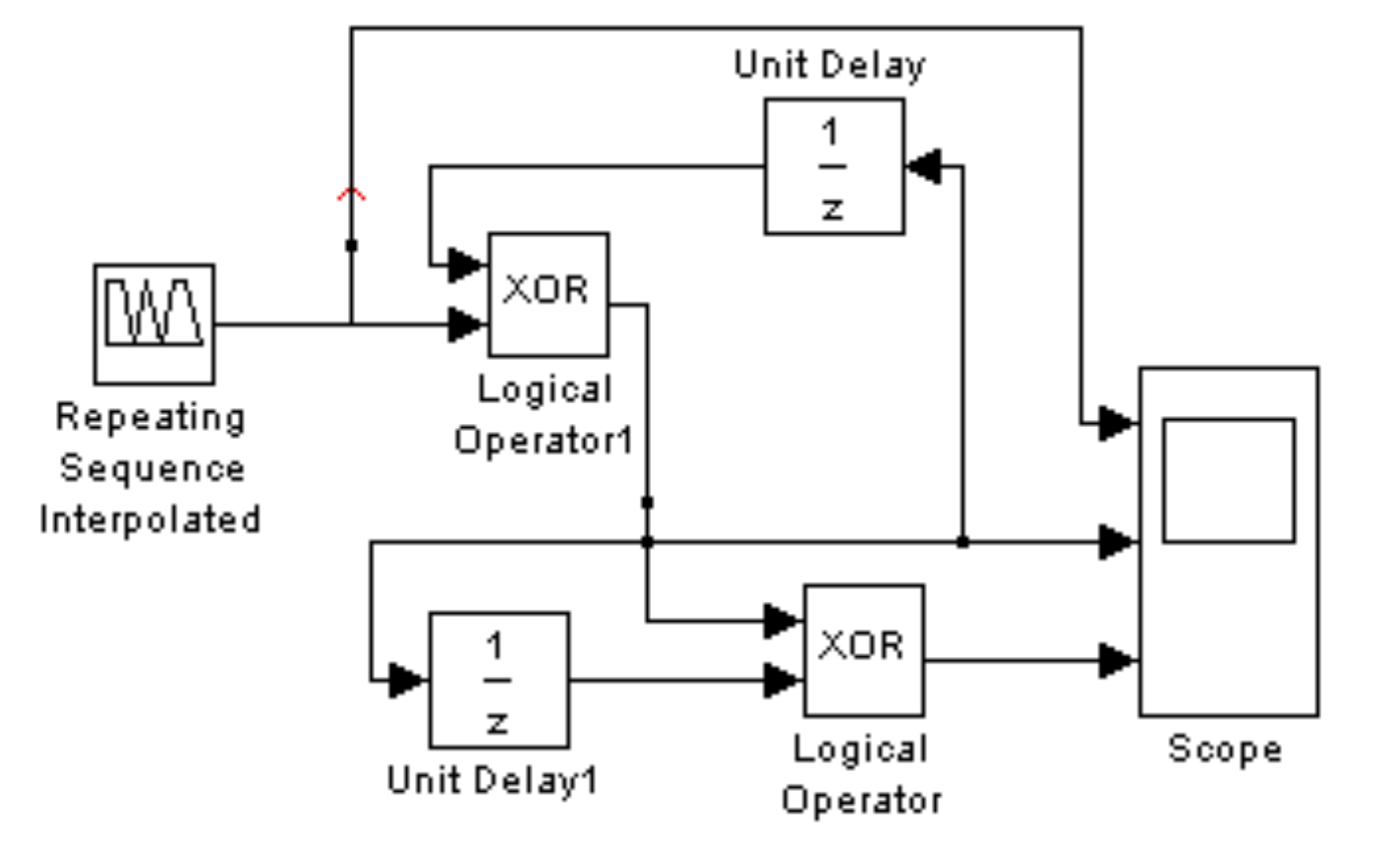
Рис. 4.6. Модель формирования дифференциальной фазовой манипуляции, построенная в системе SIMULINK

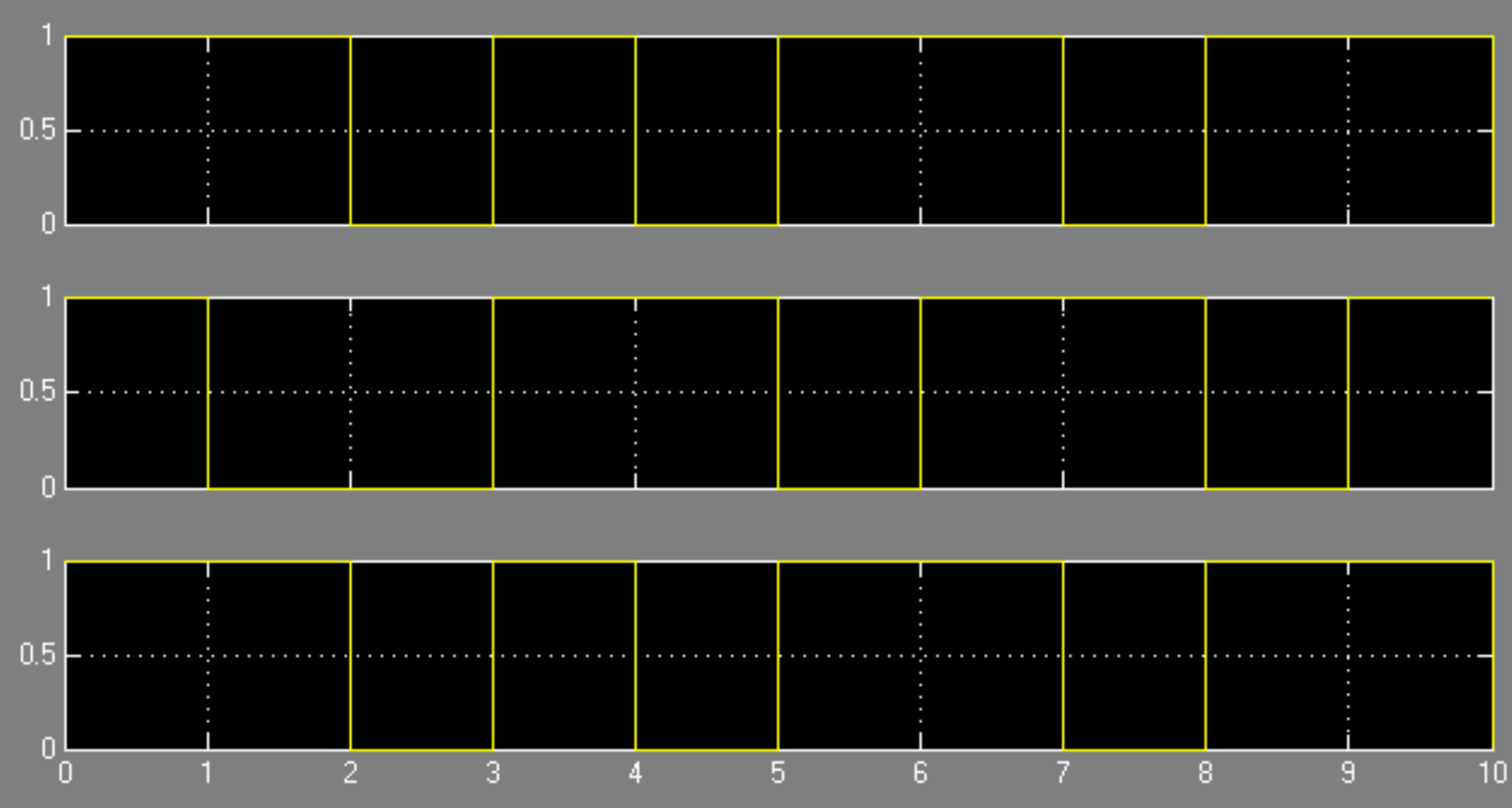
Рис. 4.7. Осциллограммы исходного сигнала с фазовой манипуляцией (верхний рисунок), сигнала с дифференциальной фазовой манипуляцией (средний рисунок) и обратно преобразованного сигнала с дифференциальной фазовой манипуляцией в сигнал с фазовой манипуляцией (нижний рисунок)

Моделирование преобразований по алгоритмам (4) и (6) можно выполнить и в системе MatLAB. Для этого необходимо создать m-файл, с помощью которого будет реализована процедура перекодировки по алгоритмам (4) и (6):

%m-файл процедуры перекодировки

%входная последовательность

a = [1101010100];

%выходная последовательность

aout = a(1);

I = 1;

for i= 5

aout (i) = xor(a(i), aout(i-1));

end

aout

%вывод выходной последовательности в командное окно

b(1) = aout(1);

for I = 2:5

b(i) = xor(aout(i-1), aout(i))

end

b

%вывод обратного преобразования последовательности в командное окно

Выполняя этот m-файл легко убедиться, что результат выполнения соответствует данным, изображенным в командном окне.

Частотно-манипулированные сигналы с разрывной

и непрерывной фазой

Частотная манипуляция FSK или, иначе, частотная модуляция с разрывной фазой, имеет место при скачкообразном изменении несущей частоты на некоторую величину в соответствии с величиной импульсов цифрового модулирующего сигнала.

В общем случае каждый передаваемый k-й импульс M-позиционной FSK записывается в виде:

, (1)

где g_k(t) = exp[iφ_k(t)] = exp(i2πf_dt), w_k = A_kq(t), A_k = 2k – 1– M для k = 1, 2, …, M, f_d – девиация частоты, q(t) – форма модулирующего импульса.

Частотно-модулированные сигналы, определенные согласно (1), не гарантируют непрерывность фазы сигнала при изменении частоты. Фазовые скачки, очевидно, приводят к избыточному расширению ширины спектра модулированного колебания. Вследствие разрывности фазы достаточно сложно и вычислить спектральную плотность мощности для таких сигналов. Поэтому на практике значительно чаще применяют частотные методы модуляции, обеспечивающие непрерывность фазы при изменениях частоты. Методы непрерывной частотной модуляции не требуют никаких дополнительных аппаратурных затрат для реализации по сравнению с обычной FSK.

Идея осуществления модуляции с непрерывной фазой естественно следует из требования максимально возможного уменьшения ширины спектра сигнала. Очевидно, что любые разрывы и резкие изменения какого-либо параметра несущей автоматически приводят к избыточному расширению спектра. Под избыточным расширением понимается увеличение ширины спектра сигнала, которое не приводит ни к увеличению пропускной способности канала, ни к повышению достоверности приема. Одним из способов уменьшения избыточной полосы сигнала является применение фильтров сглаживания сигналов. Действительно, нет никакой необходимости передавать хорошо прямоугольные импульсы сигнала, занимающие относительно широкий диапазон частот. Вполне достаточно использовать сглаженные сигналы с более узкой занимаемой полосой частот, если хотя бы в отдельные, выделенные моменты времени импульс сохраняет свою первоначальную амплитуду. Измеряя амплитуду сигнала именно в эти моменты времени, мы не теряем информации, но в то же время, используем меньшую полосу частот.

После «сглаживания» импульсов модулирующего сигнала естественно применить «сглаживание» и для метода модуляции, т.е. исключить резкие скачкообразные изменения модулируемого параметра.

Возвращаясь к общей форме записи частотно модулированного сигнала (34), потребуем, чтобы фаза комплексной огибающей была непрерывной функцией времени. Непрерывность фазы будет наверняка обеспечена в том случае, если закон изменения фазы будет интегральной функцией времени. В этом случае любая физически реализуемая функция времени, стоящая под интегралом, будет удовлетворять условиям Дирихле, а, следовательно, и интеграл от этой функции будет непрерывной функцией времени:

, (2)

где A_k – символы информационной последовательности, q(t) – форма импульса.

Существенно, что под интегралом стоит сумма всех предыдущих переданных символов, поскольку только учет предыдущих состояний фазы модулированного сигнала позволяет обеспечить ее непрерывность. Во всех предыдущих случаях (при фазовой манипуляции или FSK) текущее значение фазы зависело только от текущего значения модулирующего символа.

Меняя местами линейные операции суммирования и интегрирования, уравнение (2) можно преобразовать к виду:

(3)

Первое слагаемое отражает суммарный набег фазы за все время передачи символов сообщения, второе слагаемое отражает текущий набег фазы на последнем символьном интервале.

Для прямоугольного импульса модулирующего сигнала (q(t) = const):

, (4)

где h = 2f_dT_S – индекс модуляции

Для каждого предшествующего импульса, кроме текущего, результат интегрирования прямоугольного импульса на интервале времени T_S, равном длительности символа, дает величину T_S, так что набег фазы на k-м символьном интервале определяется произведением . В момент окончания предпоследнего импульса текущее значение фазы определяется первым слагаемым, второе равно нулю. Затем, при скачкообразном переходе от передаваемого символа к , фаза, описываемая вторым слагаемым, начинает плавно изменяться от 0 до значения .

Уравнения (2)÷(4) для фазы сигнала и комплексной огибающей g(t) определяют общий вид частотно-модулированного сигнала с непрерывной фазой. Из этих уравнений следует, что частотная модуляция с непрерывной фазой является нелинейной модуляцией с памятью. Нелинейность модуляции заключается в том, что комплексная огибающая передаваемого символа не определяется только текущим значением передаваемого символа, а зависит от времени и предыдущих переданных символов. Следовательно, принцип суперпозиции, который справедлив для линейных амплитудной и фазовой модуляций, не выполняется для частотной модуляции с непрерывной фазой. Необходимость элемента памяти очевидно необходима для обеспечения непрерывности изменения фазы.

Приведем без вывода полезную формулу для спектральной плотности мощности ЧМ сигнала с непрерывной фазой и прямоугольной формой импульсов информационной последовательности:

(5)

где h – индекс модуляции, M – количество уровней информационной последовательности, T – длительность символьного интервала, f – частота,

.

В качестве примера на рис. 5.4 показана спектральная плотность мощности частотно модулированного сигнала при модуляции бинарным сигналом (M = 2) прямоугольной формы в зависимости от нормированной частоты при индексах модуляции h = 0,25, 0,5, 1.

Наглядным методом анализа свойств частотно модулированных сигналов являются фазовые траектории (рис. 5.5). Предположим, что модулирующий сигнал представляет собой бинарную последовательность , форма модулирующего импульса прямоугольная. При этих условиях фаза модулированного сигнала изменяется линейно на интервале времени T. Значками +1 или –1 на фазовой диаграмме (фазовом дереве) обозначены значения амплитуды модулирующего сигнала. Фазовая диаграмма является кусочно-линейной функцией времени, хотя информационные символы изменяются скачкообразно. Диаграмма фактически указывает все возможные состояния фазы модулированного сигнала при произвольных значениях информационных символов.

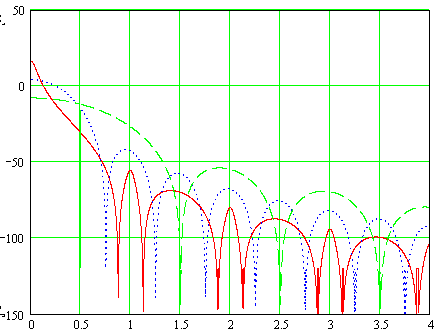
Рис. 5.4 Спектральная плотность мощности частотно

модулированного сигнала

Спектрально-эффективная частотная манипуляция

Для сигнала с непрерывной фазой и равенство справедливо при минимальном значении аргумента, равном :

(7)

Отметим, что для сигналов с разрывной фазой ортогональность сигналов имеет место при минимальном фазовом сдвиге, равном :

(8)

Таким образом, MSK сигнал имеет в два раза большую спектральную эффективность, чем сигнал с разрывной фазой при равной вероятности достоверного приема. Этот вывод подтверждается и расчетом спектральной плотности частотно модулированных сигналов рис. 5.15. Ширина спектра сигнала с индексом модуляции имеет минимальную величину по сравнению с сигналами с или .

Математическая форма записи MSK сигнала следует непосредственно из общей формулы для непрерывно-фазовых сигналов с прямоугольной формой импульсов сигнала при h = 1/2:

(9)

Рассмотрим подробнее типовые схемы MSK модуляторов и демодуляторов.