Задача 1.

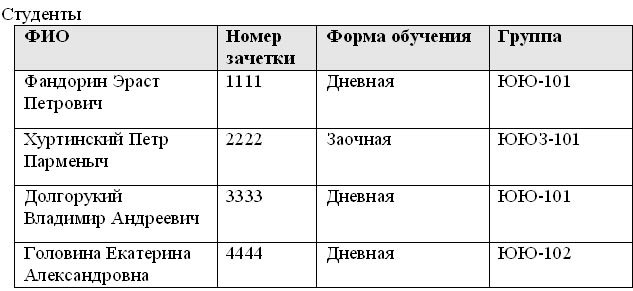
Написать запросы, которые преобразуют эту таблицу в эквивалентную(ные) во 3-ей НФ – вместе с данными.

Задача 2

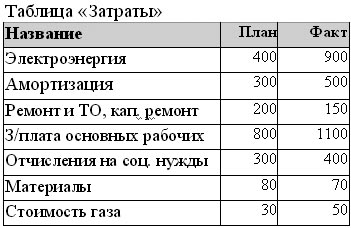
Написать запрос для вывода пункта затрат, где было максимальное превышение плана.

Т.е. результатом должно быть: Электроэнергия, превышение плана = 500

Список литературы:

1. Базы данных: модели, разработка, реализация / Т, С. Карпова. — СПб.: Питер,2001. Имеется электронный вариант в НБ ЧелГУ. 2. М.Р. Когаловский. “Энциклопедия технологий баз данных”. М. Финансы и статистика, 2002. Имеется в НБ ЧелГУ, в количестве 2 шт. 3. К. Дейт. “Введение в системы баз данных”. 7-е изд., М.; СПб.: Вильямс.- 2007. Имеется в НБ ЧелГУ в количестве 35 шт.

4. Пушников А.Ю. Введение в системы управления базами данных [www.citforum.ru/dbms]

Методы оптимизации и исследование операций

Теория:

1. Задача линейного программирования и различные формы ее записи. Приведение общей задачи ЛП к симметричной форме записи.

2. Приведение общей задачи ЛП к каноническому виду.

3. Условие оптимальности базисного плана канонической задачи ЛП. Симплекс-метод и его сходимость.

4. Теорема о существовании решения задачи ЛП.

5. Формулы пересчета при симплекс-методе.

6. Построение начального базисного плана с помощью искусственных переменных.

7. Двойственность для задач линейного программирования в симметричной форме записи. Критерии оптимальности.

8. Запись двойственной задачи и условий дополнительности для задачи ЛП общего вида.

9. Обзор методов нелинейной оптимизации. Метод возможных направлений.

10. Градиентные методы нелинейной оптимизации.

11. Методы штрафных функций и функций Лагранжа для нелинейной оптимизации.

12. Транспортная задача в матричной постановке. Существование решения. Критерий оптимальности для транспортной задачи. Метод потенциалов. Связь с симплекс-методом.

13. Динамическое программирование. Принцип оптимальности Беллмана. Функциональное уравнение динамического программирования на примерах. Особенности применения динамического программирования.

14. Целочисленное линейное программирование. Общие замечания. Схема метода ветвей и границ для дискретных задач оптимизации.

15.  Системы массового обслуживания. Их общая характеристика.

16. Математическая модель однофазной СМО.

17. Показатели эффективности системы массового обслуживания

18. СМО с конечной очередью. Определение вероятностей состояний.

19. Показатели эффективности СМО с конечной очередью.

20. СМО с отказами. Определение вероятностей состояния.

21. Показатели эффективности СМО с отказами.

22. СМО с ожиданием. Определение вероятностей состояний.

23. Показатели эффективности СМО с ожиданием.

Практика:

Задача 1.

Для производства двух видов продукции А и В используются три вида ресурсов. На изготовление единицы изделия А расходуется a₁ , a2 и a₃ кг ресурсов соответствующего вида, на изготовление единицы изделия В расходуется b₁ , b2 и b₃ кг ресурсов .

На складе фирмы наличные объемы ресурсов соответствующего вида составляют c₁ , c2 и c₃ кг.

От реализации единицы готовой продукции вида А фирма имеет прибыль в размере  рублей, а от единицы продукции вида В -  рублей.

Требуется найти такие объемы производства продукции А и В, при которых достигается максимум суммарной прибыли от реализации. При этом количество используемых ресурсов на производство продукции не должно превосходить их наличного количества.

1. Запишите соответствующую вашему варианту числовую модель задачи линейного программирования

2. Найдите решение задачи симплекс – методом.

3. Дайте геометрическую интерпретацию полученного решения.

4. Запишите сопряженную задачу и найдите ее решение из соотношений двойственности.

5. Поясните экономический смысл полученного решения сопряженной задачи.

a1 a2 a3 b1 b2 b3 c1 c2 c3   20 15 14 28 9 1 758 526 541 10 2

Задача 2.

Имеются три пункта производства, располагающие некоторым однородным продуктом в количествах a₁, a₂ и a₃. Продукт необходимо доставить в пять пунктов конечного потребления, платежеспособный спрос в которых составляет b₁, b₂, b₃, b₄ и b₅. Затраты на транспортировку (прямую поставку) единицы продукта от пункта производства в пункт потребления приведены в таблице С. Требуется отыскать такие объемы прямых поставок продукта от пунктов производства к пунктам потребления, при которых достигается минимум суммарных транспортных затрат.

a1	a2	a3	b1	b2	b3	b4	b5	C
200	175	225	100	130	80	190	100	5 7 4 2 5 7 1 3 1 10 2 3 6 8 7

ЛИТЕРАТУРА

1. Ашманов С.А. Линейное программирование. М.:Наука, 1981.

2. Сухарев А.Г., Тимохов А.В., Федоров В.В. Курс методов оптимизации. М.:Наука, 1986.

3. Карманов В.Г. Математическое программирование.– 5-е изд. М.:Физматлит, 2001.

4. Мину М. Математическое программирование. М.: Наука, 1990.

5. Галкина В.А. Дискретная математика: комбинаторная оптимизация на графах. М.:Гелиос АРВ, 2005.

6. Таха, Х.А. Введение в исследование операций. 7-е изд – М.: Издательский дом «Вильямс», 2007.