Тема 5. Дополнительные сведения о логических функциях
В этом разделе собраны различные полезные сведения, которые рано или поздно приходится использовать при построении логических схем.
Если в заданной таблице истинности число единиц составляет более половины общего числа строк, то сократить работу по минимизации можно за счёт того, что строить не саму функцию, а её инверсию – попросту говоря, добавить ещё один столбец, куда записать 1 в той строке, где был 0 в столбце F и наоборот. Число единиц теперь окажется существенно меньше. Построив схему для инверсной функции, надо не забыть подключить к её выходу инвертор для восстановления первоначального смысла функции.
Может случиться и так, что функция будет задана не для всех наборов исходных переменных-аргументов, которые перечислены в таблице истинности. Пусть в каком-либо календарном устройстве воскресенье кодируется как 000, понедельник – как 001 и так далее до субботы – 110. Больше дней недели нет, комбинация 111 осталась неиспользованной. При правильной работе устройства на вход блока, включающего световое табло «Сегодня мастерская не работает», никогда не будет поступать этот код 111. Для того, кто задаёт таблицу, значение функции на этом наборе безразлично.
Такого рода функции называют недоопределёнными или частично определёнными. В таблице истинности на местах неопределённых значений обычно ставят прочерки. Непосредственно построить СДНФ, а значит, и схему для такой функции нельзя. Функцию сначала надо доопределить – то есть самостоятельно заполнить позиции прочерков нулями либо единицами. Как правило, это делают так, чтобы достичь лучшей минимизации. Удобно это делать непосредственно в карте Карно – сначала перенести туда из таблицы истинности не только все нули и единицы, но и все прочерки, затем заполнить позиции прочерков так, чтобы объединялось возможно большее количество единиц.
В конструкциях цифровых устройств часто находит применение ещё одна базисная функция, которую в настоящее время можно считать стандартной. Она называется «сумма по модулю 2». В случае двух (и только двух!) аргументов эта же функция именуется «Исключающее ИЛИ», «Неравнозначность», NAND. Таблица истинности этой функции была приведена выше (Тема 1). Название связано с тем, что функция в точности совпадает с результатом арифметического сложения двоичных чисел в пределах одного разряда. Отсюда широкое применение этой функции при построении разного рода счётных и суммирующих устройств, а также устройств контроля правильности передачи данных. Ниже приведено условное изображение элемента, реализующего эту функцию, и её представление в базисе И, ИЛИ, НЕ:
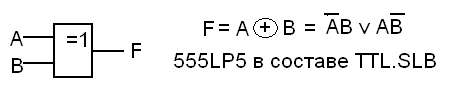
Если используемый логический базис дополнить этим элементом, то зачастую удаётся более экономно строить логические устройства для тех функций, которые не минимизируются или плохо минимизируются в базисе И, ИЛИ, НЕ.
Серия интегральных микросхем (ИМС) – это группа ИМС, одинаковых или схожих по используемым технологиям и имеющих одинаковые (совместимые) уровни входных и выходных сигналов, рассчитанные для совместного применения в аппаратуре. Серия, как правило, обозначается номером (например, 155, 555 или 176), а отдельные изделия – логические элементы и более крупные узлы – обозначаются сочетанием букв и цифр, например, 155ИР17 или 176ЛА1.
В библиотеке TTL.SLB размещаются модели элементов серии 555. Это отечественная серия, и её компоненты изначально обозначались русскими буквами. Однако, поскольку в библиотеках PCAD русские обозначения не допускаются, то и все обозначения, находящиеся там, получены транслитерацией (заменой русских букв на английские). Так, элемент 555ЛА3 обозначен как 555LA3, 555ИЕ7 – как 555IE7 и так далее.
Справочные данные по элементам, используемым в практикуме, и их условным обозначениям приведены в отдельном методическом пособии, которое имеется в компьютерном кабинете. Здесь же отметим, что набор логических элементов серии 555 отнюдь не исчерпывается только элементами И, ИЛИ. НЕ. Серия 555, как и другие, содержит не минимальный, а расширенный базис элементов, что позволяет более рационально строить схемы многих цифровых устройств.
Важнейшими элементами этого расширенного базиса являются инвертирующие функции (и соответственно элементы) И-НЕ и ИЛИ-НЕ. Любая из этих функций сама обладает полнотой, то есть способностью выражать какие угодно сложные логические функции только через саму себя. Таблицы истинности этих функций были приведены выше (Тема 1). Особенно часто используется сочетание элементов (функций) НЕ и И-НЕ. Есть в серии 555 и ещё более мощные комбинированные элементы, например, 555ЛР11.
Логический элемент И-НЕ обозначается подобно элементу И, а элемент ИЛИ-НЕ – подобно элементу ИЛИ, но с очень важным (!) отличием: на выходе элемента изображается кружок – символ инверсии, как у элемента НЕ. Чтобы грамотно работать в инвертирующих базисах, надо знать логические тождества, известные как правила де Моргана.
Правила де Моргана для случая двух аргументов изображаются следующими формулами:
Формул всего две, запись справа и слева означает (по закону двойного отрицания) по сути одно и то же и приведена здесь лишь для удобства использования.
Элементы И-НЕ более эффективно реализуются интегральной технологией, чем чистые И, а также ИЛИ, поэтому после построения и минимизации логической функции имеет смысл перевести полученную формулу в базис НЕ, И-НЕ и реализовать на ИМС серии 555 именно в таком виде.