Тема 4. Минимизация (упрощение) логических функций
Представление логической функции в виде СДНФ, рассмотренное выше, не единственно возможное и, как правило, не самое короткое. Чаще всего подобную формулу удаётся упростить или, как принято говорить в алгебре логики, минимизировать. Этот процесс аналогичен упрощению обычных алгебраических выражений. Безусловно, всем студентам физического факультета памятны задачи из школьного курса алгебры под общим названием «Упростить выражение», например:
Мы применили здесь известное тождество квадрата суммы и приведение слагаемых с разными знаками. Что же может предложить нам алгебра логики? Наиболее очевидный способ состоит также в последовательном применении к исходному логическому выражению (СДНФ) различных логических тождеств. Этих тождеств существует довольно много, часть из них аналогична законам обычной (классической) алгебры, другие же весьма специфичны. Автор данного пособия не планирует превращать последнее в учебник математической логики, поэтому ниже будут приведены лишь самые основные тождества, без которых, что называется, нельзя жить. Остальные тождества можно найти в более подробной учебной литературе.
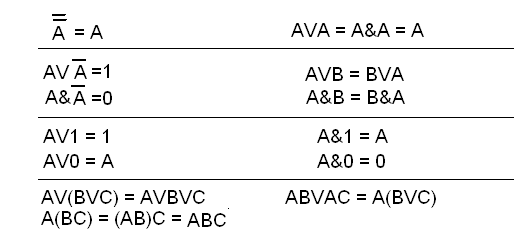
Процесс минимизации состоит в том, что к исходной СДНФ применяются эти и другие подобные тождества до тех пор, пока это возможно. Возьмём, например, ранее рассмотренную функцию (Тема 2) и преобразуем её:
В результате получилась более короткая формула, чем исходная СДНФ, соответственно и логическая схема будет проще. Попробуйте построить её самостоятельно.
Кроме непосредственного применения логических тождеств, существуют и другие методы минимизации. В частности, довольно широко используется наглядное геометрическое представление функции трёх переменных в виде объёмной фигуры – куба. Предполагается, что куб построен с началом системы координат, расположенном в одной из вершин куба. Сами оси координат, на которых отмечены только значения 0 и 1, представляют ни что иное как значения исходных переменных-аргументов A, B, C:
Функция принимает восемь значений – у куба как раз восемь вершин. Каждая вершина изображается либо закрашенным (тёмным) кружком, если соответствующее значение функции равно 1, либо никак не отмечается, если значение равно 0. Соседние вершины, образующие одно ребро, можно склеить, представив это ребро в формуле двучленной конъюнкцией, что равнозначно применению формулы
¬ABC V ABC = BC · (¬A V A) = ВС.
Ещё лучше, если найдутся вершины, образующие целую грань – тогда можно склеить все четыре вершины, представив эту грань в итоговой формуле как одну-единственную переменную (либо её инверсию). Лишь вершины, не имеющие соседей, придётся оставить в таком виде, как они и были – в виде трёхчленных конъюнкций.
Существует и модификация этого представления для случая функции четырёх переменных – четырёхмерный гиперкуб, который в данном случае наглядно изображают в виде двух кубов, один из которых «вложен» в другой (находится внутри другого). У такой фигуры 16 вершин, отвечающих 16 значениям функции. Работа с такой фигурой выглядит уже довольно громоздко.
Дальнейшее развитие геометрического представления привело к появлению очень удобного метода диаграмм Вейча, или метода карт Карно, основанного на зрительном анализе развёрток многомерных кубов на плоскости, Карта Карно – это плоская таблица из восьми клеток для функции трёх переменных и из шестнадцати клеток – для функции четырёх переменных. Значения нулей и единиц над столбцами и слева от строк здесь располагаются так, чтобы при переходе от строки к строке и от столбца к столбцу всегда изменялось значение только одного разряда:
В такую таблицу сначала переносят все значения функции из таблицы истинности (все нули и единицы из столбца F), а затем приступают к построению контуров (обводов) единиц, Единицы, стоящие рядом в количестве 2, 4, или 8 и образующие один вертикальный, один горизонтальный отрезок (прямоугольник) либо квадрат, обводят общим контуром. Одна и та же единица может входить в несколько контуров:
Для каждого такого контура выписывают конъюнкцию переменных-аргументов по принципу: переменная, значение которой изменяется (с 0 на 1 или наоборот) внутри контура, НЕ ВХОДИТ в конъюнкцию (слагаемое будущей ДНФ). Сколько было контуров – столько получится и слагаемых (с учётом ни с чем не объединённых единиц). Останется только соединить эти слагаемые знаками «ИЛИ».