Инструментальные методы рб

9 Семестр лекции 17 ч зачёт

Общие свойства детекторов. Функция отклика, форма линии. Временное и энергетическое разрешения. Связь показаний детектора с полем излучений.

Спектрометрия заряженных частиц. Измерение энер­гии частиц с помощью ионизационных камер, пропорциональных счетчиков, полупроводниковых и сцинтилляционных детекторов.

Сцинтилляционная и ПП гамма- спектрометрия. Характеристики спектрометров. Методы обработки спектров.

Расчёты экспериментов по определению:

• концентрации ⁴⁰K в почве и поверхностного загрязнения ¹³⁷Cs,

• концентрации U и ^239,240Pu и определение происхождения плутония,

• концентрации трития в воде

Лабораторные работы проводятся в ФЭИ

Technical skill is the mastery of complexity while creativity is the mastery of simplicity.

E. Christopher Zeeman

Л1 05 09 13

При прохождении ИИ через вещество изменяется

вещество и излучение

1. Ии рассеивается, поглощается и генерирует новое ии þ определение параметров ии и среды.( гамма и нейтронная спектрометрия)

2. Ии изменяет состояние среды þ радикалы, кванты,

следы Þ регистрация.

3. Ии þ наведенная радиоактивность þ анализ состава.

4. Меченые атомы (T, T_1/2 = 18 кэВ)

5. Естественная радиоактивность Þ возраст (¹⁴C,T_1|2 = 5730 л, E_bmax =156кэВ , миграция).

Общие свойства детекторов

Функция отклика G(x^®,y^®) (форма линии, амплитудное распределение импульсов). Линейное приближение: амплитуда выходного сигнала пропорциональна амплитуде входного. Сдвиг по времени.

Пример: разделение V и t и G(E,V) = g(E)d(E-V) :

Статистика исключает d функцию Разрешение и основы статистики

Критерии, по которым судят о качестве детектора - это разрешающая способность (разрешение) по отношению к измеряемой величине (энергии, времени, пространственной координате и т.д.). Если истинное значение искомой величины z₀ (например, энергия гамма-кванта E₀), то детектор формирует функцию распределения D(z) от переменной z_изм - z₀, где z_изм -измеренное значение x. Ожидаемое значение <z>:

Нормированная D(x) –плотность распределения вероятности.

Дисперсия

(s_z – стандартное отклонение)

Для прямоугольного распределения

D(z) = 1 в интервале - d/2 £ z £ d/2

D(z) = 0 вне интервала

<z> = 0

s_z = d/12

δ и σ_z размерны; δz/z или σ_z/z - безразмерны.

Часто экспериментальные величины распределены нормально.

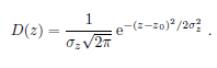
Распределение Гаусса для σ_z = 0,5, z₀ = 50 и σ_z = 1, z₀ = 50.

Для распределения Гаусса (нормального) 68.27% всех значений z находится в доверительном интервале ([z₀ − σ_z, z₀ + σ_z]), внутри ([z₀ −2σ_z, z₀ +2σ_z])- 95.45% и внутри ([z₀ −3σ_z, z₀ +3σ_z]) - 99.73% всех значений. Значения 68.27%, 95.45%, 99.73% - доверительные уровни.

Если задан доверительный уровень то вычисляется доверительный интервал и наоборот. (но только если известна D(z) !). При негауссовой D(z) доверительный интервал может быть несимметричным относительно среднего.

Для характеристики разрешения часто используют ширину на полувысоте распределения (full width at half maximum (FWHM)) -Dz.

Для нормального распределения

Распределение Гаусса непрерывно. Если регистрируются импульсы детектора, то их распределение описывается распределением Пуассона. Оно дискретно и ассиметрично (число событий (импульсов) не может быть отрицательным). Если среднее число событий μ распределение числа наблюдаемых событий n

Математическое ожидание для этого распределения равно μ, а дисперсия

σ² = μ. !!

Для больших n распределение Пуассона аппроксимируется гауссовым.

При регистрации случайного события возможны только два исхода: либо регистрация события с вероятностью p либо пропуск с вероятностью 1 – p = q. Вероятность регистрации точно r событий из общего числа n экспериментов даётся биномиальным распределением: (Bernoulli distribution)

Математическое ожидание <r> _ = n · p и дисперсия σ² = n · p · q.