Теорема 3 (Кориолиса). Абсолютное ускорение аа в сложном движении равно геометрической сумме переносного ае, относительно аr и кориолисова аk ускорений:

(1.12)

Направление Кориолисова ускорения – вектор направления скорости относительно тела к, необходимо повернуть на 90^о по направлению к угловой скорости.

, , (1.13)

где ω_е – угловая скорость переносного движения; υ_r – относительная линейная скорость; произведение ω_е и υ_r - векторное.

Объединяя утверждения теорем 1 и 2, для абсолютной скорости любой точки В можно записать следующее векторное равенство:

, (1.14)

где υ_А – скорость любой точки А рассматриваемого твердого тела; υ_ВА - относительная скорость точки В в ее мгновенном вращении вокруг точки А; линия действия этой скорости перпендикулярна радиусу ВА.

Графическое изображение скоростей в масштабе, называют планом скоростей. Точка Р_v является началом отсчета, и ее часто называют полюсом плана скоростей.

Если переносное движение – поступательное (ω_е = 0), то ускорение Кориолиса а_k = 0. Относительное движение по теореме 1 - вращение точки В вокруг точки А. Поэтому относительное ускорение а_r, в свою очередь состоит из двух ускорений: нормального аⁿ = ω²r, направленного вдоль линии ВА к центру вращения, и касательного а^t, направленного перпендикулярно ВА (рисунок 1.21, а_r = a_ВА). Таким образом, выражение (1.13) получит вид:

(1.15)

Рассмотрим векторный метод планов скоростей и ускорений на примере четырехшарнирного механизма (рисунок 1.21, а).

План скоростей. Абсолютная скорость точки А (l₁ – длина звена ОА); вектор υ_А перпендикулярен ОА и направлен по угловой скорости ω₁. Для определения абсолютной скорости точки В в соответствии с теоремой 1 рассмотрим движение звена АВ как сумму поступательного переносного движения вместе с полюсом –

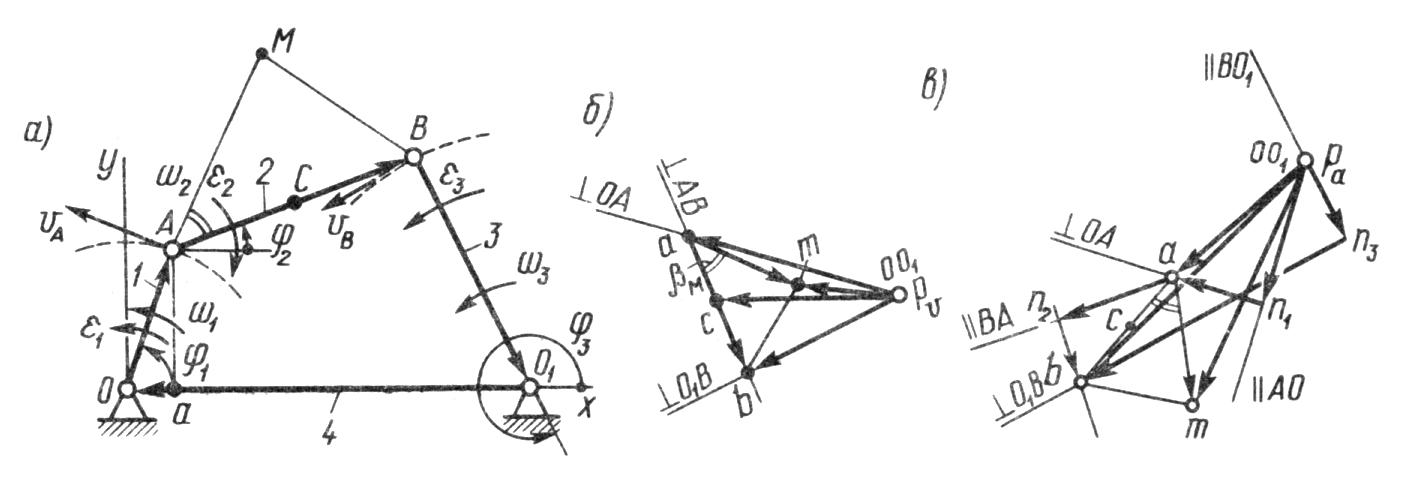
Рисунок 1.21

точкой А и относительного вращения вокруг полюса А. Векторное уравнение (8) определяет абсолютную скорость точки В; здесь линия действия вектора перпендикулярна звену О₁А, а вектора - звену АВ (в уравнении (1.14) векторы, известны по модулю и направлению, подчеркнуты дважды, а векторы, у которых известна только линия действия, - один раз). При графическом решении уравнения (1.14) на чертеже выбирают начало отсчета – точку р_υ

(рисунок 1.21, б), откладывают от нее в направлении скорости υ_А отрезок р_υa. Длину отрезка р_υa выбирают из условия удобства дальнейших построений: отрезок р_υa определяет масштабный коэффициент плана скоростей:

который показывает, что каждый миллиметр чертежа изображает μ_υ единиц скорости; единица масштабного коэффициента – (м/с)/мм.

Продолжая графическое решение уравнения (1.14), из точки а плана (рисунок 1.21, б), которая изображает конец вектора υ_А, проводим линию действия вектора υ_ВА перпендикулярную АВ, а через начальную точку р_υ – линию действия вектора υ_В перпендикулярного О₁В. Точка b пересечения этих линий определяет отрезок р_υb, изображающий вектор υ_В. Отрезок ab изображает вектор υ_ВА; согласно уравнению (1.14) направление этого вектора – от точки а к точке b. Векторный треугольник р_υab - графическое решение исходного уравнения; модули найденных векторов скоростей:

Угловые скорости звеньев 2 и 3 в их движении относительно точек А и О₁:

где l₂ = АВ, l₃ = ВО₁ – длины соответствующих звеньев. Для определения направления угловых скоростей ω₂ и ω₃ векторы и переносим мысленно с плана скоростей на план механизма в точку В и видим, что звено 2 вращается относительно точки А по часовой стрелке, а звено 3 относительно точки О₁ – против часовой стрелки (рисунок 1.21, а).

Определив скорость точки В, скорости точек С и М (или любых других в данном положении механизма) находят без составления уравнений и их решения; для этого используются следующие свойства планов скоростей и ускорений:

1. Векторы, идущие из точки р_υ плана скоростей (ускорений), представляют собой в масштабе μ_υ абсолютные скорости (ускорения) соответствующих точек механизма; векторы, не проходящие через полюс, есть относительные скорости (ускорения) точек звеньев. Концы векторов абсолютных скоростей (ускорений) точек А, В, … принято обозначать соответствующими малыми буквами а, b, … .

2. Отображения точек закрепленных шарниров О, О₁ всегда совпадают с начальной точкой р_υ.

3. Отрезки оа, ab, o₁b на плане отображают звенья АО, АВ и О₁В механизма. Это означает, что если, например, на звене АВ

(рисунок 1.21, а) имеется точка С, лежащая на прямой АВ, то соответствующая отображающая точка с на плане (рисунок 1.21, б) находится на прямой ab и при этом верно соотношение ab/ac=l₂/АС, что вытекает из уравнений тогда вектор абсолютной скорости точки с звена 2

4. Любые три точки А, В, М звена, составляющие треугольник, отображаются на плане в треугольник Δabm подобный ΔАВМ; на отрезке ab можно построить два треугольника, подобных данному; из них искомое решение дает тот, у которого порядок обхода вершин из точки а такой же, как в ΔАМВ (направление обхода вершин на звене и на плане должно быть одинаковым). Таким образом, на рисунке 1.21, б получено отображение на плане точки М – точки m:

При тщательном выполнении построений, средняя ошибка определения скоростей составляет 5…7%, ускорений – до 10%.

План ускорений. Исходными данными для построения плана ускорений механизма (рисунок 1.21, а) являются известные абсолютные ускорения точки А звена 1 и найденные скорости. Ускорение точки А при равно векторной сумме нормального ускорения , направленного от точки А к точке О, и касательного .

Выбрав начало отсчета р_υ плана ускорений (рисунок 1.21, в), показывают на чертеже отображения ускорений и векторы и ; вектор плана изображает полное ускорение а_А. Масштабный коэффициент плана ускорений [(м/с²)/мм]:

Для определения ускорения точки В рассмотрим абсолютное движение звена АВ как сумму переносного и относительного движений. С учетом выражения (1.15) векторной уравнение абсолютного ускорения точки В получит вид:

. (1.16)

Вектор нормального ускорения по модулю равен и как центростремительный направлен по прямой АВ от точки В к центр относительного вращения – точке А. Вектор касательного ускорения перпендикулярен прямой АВ. В уравнении (1.16) двумя чертами подчеркнуты ускорения, известные по модулю и направлению, а одной чертой – когда известна лишь линия действия. Так как ни модуль, ни линия действия вектора a_B неизвестны, а у вектора известна только линия действия, то векторное ускорение (1.16) решить нельзя; поэтому необходимо иметь второе векторное уравнение.

Точка В принадлежит одновременно звеньями АВ и ВО₁ (рисунок 1.21, а). Рассматривая движение звена ВО₁ и принимая за полюс неподвижную точку О₁, запишем следующее уравнение для абсолютного ускорения точки В:

, (1.17)

где вектор параллелен ВО₁; линия действия вектора

Совместное решение векторных уравнений (1.16) и (1.17) дает возможность определить искомый вектор абсолютного ускорения точки В. Отрезок представляет собой первое слагаемое векторного уравнения (1.16) - ускорение а_А. От точки а откладывают отрезок , изображающий вектор , который направлен параллельно звену ВА от точки В к точке А (так как звено 2 вращается относительно точки А, а вектор - центростремительное ускорение). Далее через конец отрезка an₂ проводят линию действия .

Аналогично, графически реализуется уравнение (1.17). На пересечении линий действия векторов и находится искомая точка b; отрезок изображает вектор а_В; отрезки и изображают соответственно векторы и . Полученный план ускорений и система уравнений (1.16) и (1.17) взаимно однозначно соответствуют друг другу, т.е. найденное графическое решение удовлетворяет исходным уравнениям. Стрелки векторов на плане ускорений поставлены в соответствии с векторными уравнениями.

Если на звене имеется дополнительная точка, например, на звене 2 точка С, то ее отображение с на плане ускорений (рисунок 1.21, в) находится на отрезке ab с учетом соблюдения условия .

Отображение m точки М строится на основании четвертого свойства планов: подобен ; .

Угловые ускорения звеньев в их относительном вращательном движении можно найти, используя соответствующие касательные ускорения: ; .

Для определения направления углового ускорения ε₂ звена АВ переносим вектор в точку В (рисунок 1.21, а) на плане механизма и видим, что вектор поворачивает звено вокруг точки а по часовой стрелке. Сопоставляя направления ω₂ и ε₂, заключаем, что звено 2 движется относительно точки А ускоренно. Аналогично определяем направление ускорения ε₃ звена О₁В.

60