18

Лекция 7. Физические явления в p-n-переходе

Электронно-дырочные переходы

Однородные полупроводники и однородные полупроводниковые слои находят весьма узкое применение: они непосредственно используются только в разного рода резисторов. Основные же элементы ИС (и основная масса дискретных полупроводниковых приборов) представляют собой сугубо неоднородные структуры. Два важнейших варианта таких структур это следующие: p-n-переход (контакт двух полупроводников с разным типом проводимости); структура МП (контакт металла и полупроводника).

В полупроводнике с областями p- и n- типов, образующими переход, можно выделить следующие пространственные области: металлургический переход (контакт) (воображаемая плоскость, разделяющая p- и n-области), область перехода, или область пространственного заряда, или обедненная область (располагается по обе стороны металлургического перехода и имеет толщину от 10^-6 до 10^-4 см в зависимости от технологии производства), нейтральные области (р- и n-области), лежащие между областью пространственного заряда и границами полупроводников p- и n-типов, и, наконец, омические контакты, которыми оканчиваются нейтральные области.

Электронно-дырочные переходы классифицируют по резкости металлургической границы и по соотношению удельных сопротивлений слоев.

Ступенчатыми переходами называют переходы с идеальной границей, по одну сторону которой находятся доноры с постоянной концентрацией N_d, а по другую – акцепторы с постоянной концентрацией N_a. Такие переходы наиболее просты для анализа.

Плавными переходами называют такие, у которых в районе металлургической границы концентрация одного типа примеси постепенно уменьшается, а другого растет. Сама металлургическая граница в этом случае соответствует равенству примесных концентраций (N_d = N_a).

По соотношению концентраций примесей в p- и n-слоях переходы делят на симметричные, несимметричные и односторонние. Симметричные переходы характерны условиям N_dn  N_ap, где N_dn и N_ap – концентрации примесей в соответствующих слоях.

Симметричные переходы не типичны для полупроводниковой техники.

В случае резкой асимметрии, когда концентрации примесей (а значит, и основных носителей) различаются на 1-2 порядка и более, переходы называют односторонними и обозначают n⁺ - p или p⁺ - n, где верхний индекс «+» соответствует слою со значительно большей концентрацией.

Диаграмма энергетических зон равновесного p−n-перехода

Рассмотрим равновесную модель резкого, или ступенчатого, p−n-перехода, в котором концентрация примесных атомов скачком изменяется от значения N_a в р-области до значения N_d в n-области. Резкий переход не является структурой, типичной для современных приборов. Тем не менее, такая упрощенная модель позволяет проанализировать наиболее важные характеристики, например вольт-амперные. Другая причина, позволяющая воспользоваться столь простой моделью, заключается в том, что внутренние физические процессы и электрические свойства перехода лишь в малой степени зависят от способа его изготовления.

Будем рассматривать p−n переход в состоянии термодинамического равновесия, т. е. при отсутствии внешних воздействий, таких, как внешнее напряжение. Математическая модель перехода строится на базе таких понятий, как высота потенциального барьера (контактная разность потенциалов) φ₀, толщина области перехода W, максимальная напряженность внутреннего электрического поля E_max и плотность электрического заряда Q.

Следствием предположения о термодинамическом равновесии является то, что:

- суммарные токи электронов и дырок в каждой точке объема полупроводника равны нулю (I_n=I_p=0);

- уровень Ферми постоянен для всего полупроводника.

При этом энергетические зоны изогнуты и полностью заполнены во всех точках полупроводникового материала, в которых np = n_i² .

Кроме того, принимается гипотеза обеднения, состоящая в том, что весь полупроводник с p−n-переходом мысленно разбивают на область перехода и на две нейтральные области. При этом в области перехода пренебрегают носителями заряда.

Рис. 7.1. Одномерная модель резкого p-n-перехода: xp и xn – границы области пространственного заряда, имеющей на практике толщину от 10-6 до 10-4 см (W = xn + xp; Wn = Xn – xn; Wp = Xp – xp)

В равновесном состоянии J_n = 0 (это условие, относящееся как к дрейфовому току, так и к току диффузии, часто служит отправной точкой построения теории). Можно записать

и получить .

Отсюда, используя соотношение Эйнштейна и равенство Е = – dφ/dx, находим

, (7.1)

где φ_Т = kT/e – температурный потенциал. Интегрируя (7.1) по х в пределах от –х_р до x_n, получаем

. (7.2)

Эта формула определяет высоту потенциального барьера p-n-перехода, равную

. (7.3)

Так как все примеси в обедненном слое считаются ионизированными, то

,

откуда находим

. (7.4)

Это соотношение определяет напряжение, которое возникает в условиях термодинамического равновесия, ведущее к прекращению диффузионного тока.

Рис.7.2. Кривая распределения потенциала, знак которого противоположен знаку изменения энергии (см. рис. 7.3). График можно получить, проведя двукратное интегрирование уравнения Пуассона (7.6)

Из уравнения Пуассона, в котором N(x) = N_d⁺ - N_a^–, следует:

. (7.5)

На основании гипотезы обеднения (p  n  0) это уравнение принимает вид

(7.6)

Здесь φ – электростатический потенциал, который соответствует выражению φ = -E_i/q; _а- абсолютная диэлектрическая проницаемость, равная _а = ₀_п, где ₀ – электрическая проницаемость вакуума, _п - относительная диэлектрическая проницаемость полупроводника.

Рис. 7.3. Диаграмма энергетических уровней EC и EV для некоторого р-n-перехода в равновесном состоянии. Квазиуровни Ферми EFp = -qφp и EFn = -qφn при равновесии совпадают с уровнем Ферми EF; φ = -Ei/q

Как можно видеть из рис. 7.1, в области перехода на отрезке –x_p  x  0 N(x) = N_a. Поэтому уравнение (7.6) принимает вид

Интегрируя его, получаем

(7.7)

Так как , то напряженность электрического поля

(7.8)

В области 0  x  x_n концентрация N(x) = N_d; тогда из уравнения (7.6) следует, что

(7.9)

(7.10)

Величина Е максимальна при х = 0 (рис. 7.4); на основании равенств (7.8) и (7.10) имеем

(7.11)

откуда

(7.12)

что является условием электрической нейтральности перехода.

В соответствии с рис. 4.1 толщина обедненного слоя перехода

W = x_p + x_n. (7.13)

Так как при х = 0 потенциал φ должен быть непрерывным, то постоянные интегрирования в выражениях (7.8) и (7.10) должны быть одинаковыми: С₁ = С₂ = С. Как следствие этого, используя формулы (7.13), (7.12), (7.4), (7.8) и (7.10), находим

. (7.14)

В соответствии с равенством (7.12) плотность заряда, отнесенного к единичной площади, по обе стороны от сечения х = 0 (рис. 7.5)

(7.15)

или

. (7.16)

Выражения (7.5), (7.11), (7.14) и (7.16) образуют математическую модель резкого p-n-перехода, находящегося в термодинамическом равновесии.

Рис. 7.4. Распределение напряженности электрического поля Е, полученное интегрированием уравнения Пуассона (7.6)	Рис. 7.5. Распределение плотности пространственного заряда, входящей в уравнение Пуассона (7.6)

Работа p-n-перехода при прямом смещении

В условиях термодинамического равновесия (при нулевом внешнем напряже­нии на p-n - переходе) токи диффузии и дрейфа уравновешивают друг друга. При пря­мом смещении, когда к выводам p-n - перехода прикладывается прямое напряжение U_пр (рис.7.6), это равновесие нарушается. В ОПЗ появляется компонент электрического поля Е_внеш, направленный встречно полю Е, образованному зарядами ионов доноров и ак­цепторов (рис.7.6). Это эквивалентно снижению потенциального барьера p-n - перехода на величину приложенного напряжения U₀ - U_пр. За счет ослабления поля в переходе уменьшаются дрейфовые токи электронов и дырок, и токи диффузии становятся преобладающими. Дырки диффундируют через переход в область n- типа, а электроны в область p - типа. Этот процесс называется инжекцией носителей. В результате инжекции возрастают концентрации неосновных носителей p_n(x) и n_p(x) по обе стороны перехода. Под действием градиента концентрации неосновные носители диффундируют вглубь об­ластей p и n - типов. По мере движения они рекомбинируют с основными носителями, поэтому вдали от перехода снова восстанавливаются равновесные концентрации неоснов­ных носителей p_n0 и n_p0 . Исчезнувшие в результате рекомбинации неосновные носители пополняются за счет диффузии со стороны p-n - перехода, а основные - за счет дрейфа со стороны омических контактов. В итоге возникает постоянный прямой ток.

Рис. 7.6. p-n-переход при прямом смещении

Найдем отношение электронного и дырочного токов через переход, считая их диффузионными

(7.17)

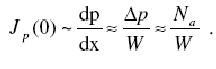
В этих выражениях Δn и Δp - перепады концентрации электронов и дырок по обе сторо­ны перехода, W - ширина ОПЗ, в пределах которой реализуются эти перепады. Таким об­разом,

В резко ассимметричных p-n - переходах N_d >> N_a или N_a >> N_d. Это означает, что инжекция в таких переходах практически односторонняя. Сильнолегированная область, из кото­рой осуществляется инжекция основных носителей, называется эмиттером. Слаболегиро­ванная область, в которую инжектируются эти носители, называется базой. Отметим, что носители, инжектированные в базу, становятся в ней неосновными.

При построении энергетических диаграмм прямосмещенного p-n - перехода необходимо иметь в виду, что условие термодинамического равновесия нарушено. В не­равновесной системе закон действующих масс, сформулированный в виде pn = n_i², не­применим, а уровень Ферми в p и n - областях не является постоянным. По этой причине вместо уровней Ферми используется понятие квазиуровней Ферми: E_Fn в области n - ти­па и E_Fp в области p - типа. Их определяют таким образом, чтобы сохранить соотношение между собственной концентрацией n_i и концентрациями электронов и дырок в том же ви­де как при термодинамическом равновесии

(7.18)

Выполнив подстановки

, , ,

представим выражения концентраций электронов и дырок в виде

, . (7.19)

В этих выражениях φ_n и φ_p называют квазипотенциалами электронов и дырок соответст­венно, φ_i - электростатическим потенциалом. Найдем произведение концентраций элек­тронов и дырок

. (7.20)

Из выражения (7.20) следует, что расстояние между квазиуровнями Ферми представляет собой меру отклонения полупроводника от состояния термодинамического равновесия. На рис.7.7, а показана диаграмма энергетических уровней прямосмещенного p-n – перехода и там же для сравнения приведена диаграмма несмещенного перехода (рис.7.7,б).

a)

б)

Рис. 7.7. Диаграммы энергетических уровней: а) p-n-перехода в равновесном состоянии; б) p-n-перехода при прямом смещении

Построение диаграммы прямосмещенного перехода выполнено в следующей по­следовательности. Первоначально произвольно устанавливается квазиуровень Ферми в одной из областей, например в р - области E_Fp. Далее он дополнен собственным уровнем Ферми E согласно выражению (7.18), в котором p = N_a, E_i - E_Fp = kTln(N_a /n_i). Так как уровень E_i располагается посредине запрещенной зоны шириной E_g, то диаграмма допол­нялась изображением дна зоны проводимости (энергия E_c) и потолка валентной зоны (энергия E_v) в области р - типа. Учитывая, что расстояние между квазиуровнями Ферми в р и n - областях равно qU, где U - приложенное напряжение, следующим шагом устанав­ливается квазиуровень Ферми в n - области E_Fn. Так же как в p - области диаграмма до­полнялась собственным уровнем Ферми E_i, а также уровнями E_c и E_v в n - области. На­конец, зоны проводимости и валентные зоны обеих областей (уровни Е_с и E_v) соединяли через область пространственного заряда (ОПЗ), ширина которой W = x_n – х_p. Напомним, что на данной диаграмме, как и на всех предшествующих, энергия электронов увеличива­ется вверх, а энергия дырок - вниз.

Вольт-амперная характеристика p-n - перехода при

прямом смещении

Уравнение Шокли

При выводе вольт-амперной характеристики (ВАХ) будем использовать обо­значения, принятые на рис.9. Для упрощения анализа примем следующие допущения.

1. В ОПЗ (-x_p< x <x_n) выполняется условие обеднения, согласно которому кон­центрации электронов и дырок в ОПЗ пренебрежимо малы. Это допущение оправдано на­личием в ОПЗ сильного электрического поля Е, которое перебрасывает подвижные носи­тели (электроны и дырки), попавшие в ОПЗ, в соответствующие нейтральные области.

2. В ОПЗ электроны и дырки не рекомбинируют. Это эквивалентно тому, что токи электронов и дырок в пределах ОПЗ неизменны. Следовательно, токи электронов и дырок на левой границе ОПЗ (х = - х_р) равны соответствующим токам на правой границе (х = х_п). Такое допущение оправдано тем, что в ОПЗ практически отсутствует накопление концентраций подвижных носителей.

3. Все внешнее напряжение U приложено к ОПЗ, так как это самая высокоомная область p-n - перехода.

4. Уровень инжекции в обеих областях низкий.

5. Генерация носителей отсутствует G_n = G_p = 0, а скорости рекомбинации электронов и дырок пропорциональны их избыточным концентрациям.

Согласно допущению 1 анализ физических процессов в ОПЗ и в нейтральных областях может производиться независимо. При в этом в ОПЗ анализируется только урав­нение Пуассона, а в нейтральных областях - только уравнения непрерывности. Вывод вольт-амперной характеристики прямосмещенного p-n - перехода связан с анализом уравнений непрерывности.

Согласно допущению 4 концентрации неосновных носителей, инжектирован­ных в p и n - области, много меньше концентраций основных носителей в этих областях. Δn_p << p_p0 ~ N_a и Δp_n << n_n0 ~ N_d. Так как в силу зарядовой нейтральности избыточные кон­центрации основных и неосновных носителей равны Δn_p = Δp_p и Δp_n = Δn_n, то пол­ные концентрации основных носителей p = p_p0 + Δp_p и n = n_n0 +Δn_n в результате инжекции практически не меняются. Вместе с тем, концентрации неосновных носителей n_p = n_p0 + Δn_p и p_n = p_n0 + Δp_n изменяются на несколько порядков. Таким образом, можно ограни­читься анализом уравнений непрерывности только для неосновных носителей.

Согласно допущению 3 электрическое поле в нейтральных областях практиче­ски отсутствует. Это позволяет пренебречь дрейфовыми компонентами в уравнениях пе­реноса, а оставшиеся диффузионные члены подставить непосредственно в уравнения непрерывности.

Согласно допущению 5 генерационные члены G_n и G_p в уравнениях непре­рывности можно опустить, а скорости рекомбинации электронов и дырок R_n и R_p пред­ставить в виде выражений

- для электронов в области р-типа

- для дырок в области n-типа

Наконец в силу того, что выводится стационарная воль-амперная характеристи­ка при постоянном напряжении смещения U, следует решать стационарные уравнения не­прерывности

.

С учетом сформулированных допущений стационарные уравнения непрерывности приводятся к виду

, (7.21)

. (7.22)

Разделим все члены уравнения (7.21) на D_n, а уравнения (7.22) на D_p и введем обозначения и . Имея в виду, что n_p0 и p_n0 являются константами, вычтем их под знаками дифференциалов в (7.21) и (7.22) соответственно из n_p и p_n. При этом уравнения (7.21) и (7.22) будут записаны относительно избыточных концентраций неосновных носите­лей Δn_p = n_p – n_p0 и Δp_n = p_n – p_n0

, (7.23)

. (7.24)

Уравнения (7.23) и (7.24) называются уравнениями диффузии, а входящие в них параметры L_n и L_p - диффузионными длинами электронов и дырок соответственно. Физи­чески диффузионная длина есть среднее расстояние, проходимое диффундирующей час­тицей (электроном или дыркой) до рекомбинации.

Для завершения математической модели процесса диффузии неосновных носи­телей необходимо сформулировать граничные условия к уравнениям (7.23) и (7.24). Так как анализ этих уравнений совершенно идентичен, ограничимся нахождением решения урав­нения (7.24) для дырок в n - области. Будем считать, что ширина нейтральной n-области превосходит диффузионную длину дырок в ней не менее чем в 3 раза: W_n > 3L_p. Тогда при удалении от перехода на две диффузионные длины концентрация инжектированных ды­рок снижается практически до равновесного значения p_n0 и перестает изменяться с рос­том координаты. Граничное условие, соответствующее данному случаю, выражается сле­дующим образом

.

Учитывая, что p_n(x) = p_n0 + Δp_n(x), это условие можно представить в более удобном виде

. (7.24а)

В качестве второго граничного условия установим соотношение равновесной и неравновесной концентраций дырок на границе ОПЗ с нейтральной n - областью (x = x_n). Согласно выражению (7.20) произведение неравновесных концентраций основных и неосновных но­сителей в точке x = x_n имеет вид

. (7.25)

Как уже отмечалось, при низком уровне инжекции неравновесные концентра­ции основных носителей в нейтральных областях практически равны равновесным. Сле­довательно n_n(x_n)  n_n0. В соответствии с законом действующих масс n_i² = n_n0p_p0. Из диаграммы энергетических уровней на рис.7.7 следует, что E_Fn - E_Fp = qU. После подста­новки указанных величин в (7.25) приходим к следующему граничному условию

, где .

Переходя к избыточной концентрации дырок Δp_n(x), полученное условие представим в виде

. (7.26)

Уравнение (7.24) является линейным, однородным дифференциальным уравнени­ем второго порядка с постоянными коэффициентами. Его решение представляет линей­ную комбинацию экспонент

. (7.27)

Постоянные интегрирования А и В находятся из граничных условий, сформулированных выше. Из граничного условия (7.24а) следует, что В = 0. При этом выражение (7.27) упрощается

. (7.28)

Постоянная интегрирования А находится из граничного условия (7.26)

.

Таким образом, распределение избыточной концентрации дырок в n - области имеет вид

при x  x_n. (7.29)

Если повторить выполненный анализ для электронов в р - области, то получим аналогичное выражение распределения избыточной концентрации электронов в р-области

при x  -x_p. (7.30)

Плотности токов электронов и дырок найдем из уравнений переноса (7.31) и (7.32) с учетом того, что согласно допущению 3 электрическое поле в нейтральных областях от­сутствует (Е = 0).

, (7.31)

. (7.32)

После подстановки в (7.31), (7.32) p_n(x) и n_p(x) из (7.29) и (7.30) найдем плотности электронного и ды­рочного токов как функции координаты

при x  -x_p, (7.33)

при x  x_n. (7.34)

Из выражений (7.29), (7.30) и (7.33), (7.34) следует, что избыточные концентрации и плотности токов неосновных носителей экспоненциально снижаются по мере удаления от перехода. Это связано с рекомбинацией носителей в процессе их диффузионного движе­ния.

На рис.7.8а в логарифмическом масштабе показаны распределения концентра­ций основных и неосновных носителей в р и n - областях. Концентрации неосновных но­сителей показаны сплошными линиями, а основных - штриховыми

а)	б)
Рис. 7.8. Распределение концентраций и плотности токов электронов и дырок в p и n – областях: а) - распределение концентраций основных (штриховые кривые) и неоснов­ных (сплошные кривые) носителей в p и n – областях; б) - плотности токов основных (штриховые кривые) и неосновных (сплошные кривые) носителей в p и n - областях

Так как анализ выполнен в предположении низкого уровня инжекции, то концентрации основных носителей p_p0 и n_n0 в результате инжекции практически не изменились. В то же время концентрации неосновных носителей по сравнению со своими равновесными значениями изменились на несколько порядков.

На рис.7.8,б сплошными кривыми показано изменение плотностей токов неос­новных носителей в р и n - областях, а штриховыми - основных носителей. В верхней части рисунка показана результирующая плотность тока через переход, которая постоянна в каждой точке х и равна сумме плотностей токов основных и неосновных носителей. На­помним, что ток инжектированных неосновных носителей является током диффузии, а ток основных носителей - током дрейфа, идущим на компенсацию рекомбинационных по­терь.

Плотность тока в каждом сечении полупроводника равна сумме электронной и дырочной составляющих в данном сечении (в данной координате x). Запишем выражение плотности тока в точке x = x_n

.

Согласно допущению 2 . Следовательно

, (7.35)

т.е. плотность тока через p-n - переход равна сумме плотностей токов неосновных носи­телей на границах ОПЗ (рис.7.1). Подставляя в (7.35) значения j_n(-x_p) из (7.33) и j_p(x_n) из (7.34), получим уравнение вольт-амперной характеристики p-n - перехода

. (7.36)

Введем обозначение и перепишем уравнение (7.36) в виде

(7.37)

Это уравнение называют формулой Шокли. Величину j_s называют плотностью тока насыщения. Важно отметить, что она определяется только параметрами полупровод­ника и не зависит от режима работы p-n - перехода (от тока через переход и напряжения на переходе). Значение j_s имеет величину порядка 10^-10 А/м².

На рис. 7.9 приведены вольт-амперные характеристики трех p-n-переходов из различных материалов.

Рис. 7.9. Вольт-амперные характеристики германиевого, кремниевого и арсенид-галлиевого p-n-переходов

Таким образом величина j_s имеет порядок 10^-10 А/см². Столь низкое значение плотности тока насыщения определяет специфику вольт-амперной характеристики перехода. Про­анализируем вид этой характеристики.

Рабочие плотности тока диодных структур имеют порядок 100 А/см². Опреде­лим из уравнения (7.37) напряжение на переходе, при котором плотность тока оказывается на три порядка меньше, т.е. 0,1 А/см² . При j_s ~ 10 А/см² для реализации указанного ус­ловия множитель ехр(U/φ_T) должен составить 10⁹. Этому соответствует напряжение U = φ_Tln10⁹ = 0,55 В. При меньших значениях напряжения ток через p-n- переход пренебре­жимо мал. Эту величину напряжения будем называть напряжением отсечки. Для кремние­вых приборов оно составляет 0,5 - 0,6 В. Отметим, что величина потенциального барьера U₀, являющегося теоретическим пределом прямого напряжения на p-n-переходе, примерно равна 0,75 В, т.е. отличается от напряжения отсечки всего на 0,2 В.

Рассмотрим температурную зависимость напряжения на прямосмещенном p-n-переходе. Пренебрежем в (7.37) единицей и выразим напряжение как функцию плотности тока

.

С ростом температуры пропорционально растет. Одновременно растет и плотность тока насыщения j_s ~ n_i² ~ . В итоге зависимость U(T) слабо выражена. С ростом температуры напряжение линейно уменьшается со скоростью 2 мВ/^оС. При этом вольт-амперная характеристика смешается в сторону меньших напряжений (рис. 7.38).

	Рис. 7.38. Вольт-амперные характеристики кремниевого p-n-перехода при температурах Т1 = 25 оС и Т2 = 125 оС