9. 2.4.5 Теоремы apt

Наиболее важные теоремы, показывающие характеристики сетей APT:

1. После стабилизации процесса обучения предъявление одного из обучающих векторов (или вектора с существенными характеристиками категории) будет активизировать требуемый нейрон слоя распознавания без поиска. Эта характеристика «прямого доступа» определяет быстрый доступ к предварительно изученным образам.

2. Процесс поиска является устойчивым. После определения выигравшего нейрона в сети не будет возбуждений других нейронов в результате изменения векторов выхода слоя сравнения С; только сигнал сброса может вызвать такие изменения.

3. Процесс обучения является устойчивым. Обучение не будет вызывать переключения с одного возбужденного нейрона слоя распознавания на другой.

4. Процесс обучения конечен. Любая последовательность произвольных входных векторов будет производить стабильный набор весов после конечного количества обучающих серий; повторяющиеся последовательности обучающих векторов не будут приводить к циклическому изменению весов.

9. 2.5 Выбор модели нейрона.

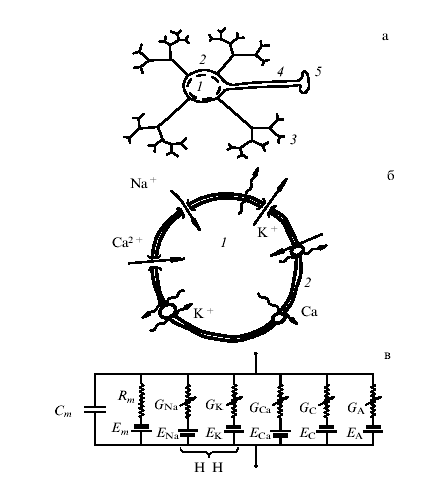
Рис. 14. (а) Схематическое изображение нейрона: 1 – тело клетки (сома), 2 – мембрана, 3 – дендриты,4 – аксон, 5 – синаптическое окончание, (б) Ионные каналы в мембране нейрона: К, Na, Са – ионы калия, натрия, кальция, (в) Эквивалентная электрическая схема мембраны нейрона: G_Na, G_K, G_Ca,…— нелинейные ионные проводимости; R_m – сопротивление утечки; С_т – емкость мембраны; E_Na, E_K,…–равновесные потенциалы для соответствующих токов.

На рис. 14 схематически изображены нервная клетка и клеточная мембрана. Для построения адекватной динамической модели нейрона принципиально, что окружающая его мембрана нередко представляет собой эквипотенциальную поверхность. Поэтому, несмотря на вполне макроскопические размеры нейрона, при анализе его электрической активности (частота 4-60 Гц) нервную клетку можно рассматривать как сосредоточенную в пространстве систему. Другими словами, переменные, описывающие состояние нейрона (мембранный потенциал, концентрацию тех или иных ионов и т.д.), можно рассматривать как функции только времени. Другой важный вопрос связан со способом описания активности нейронов. Поскольку состояние нейрона определяется неравновесной диффузией различных заряженных ионов, для моделирования его активности, вообще говоря, следует использовать кинетическое описание. Однако, когда мы интересуемся нейроном как генератором низкочастотных электрических пульсаций, такое описание, очевидно, избыточно. Для построения соответствующей теории вполне достаточно уравнений для средних по времени t₀ << Т (Т — характерный период электрической активности нейрона) динамических переменных: мембранного потенциала и макроскопических ионных токов. При этом нейрон можно рассматривать как нелинейную электрическую цепь из RC-элементов. Источником энергии для работы этой диссипативной системы служат биохимические процессы, связанные со взаимодействием внутриклеточной и межклеточной сред.

Осцилляторная активность нейрона определяется тем, что это неравновесная система с разнообразными обратными связями, в том числе и запаздывающими. Именно благодаря этим обратным связям, закрывающим или открывающим ионные каналы в соответствующей фазе электрической активности мембраны, состояние нейрона, отвечающее потенциалу покоя, может стать неустойчивым, и он превращается в генератор. Такой генератор можно рассматривать как динамическую систему, в рамках которой микроскопическая кинетика проявляется лишь как малые флуктуации.

Нелинейные динамические модели нейронов, которые строятся для объяснения обнаруживаемых феноменов и предсказания новых (в чем, собственно, и состоит назначение теории), в значительной степени зависят от того нейрофизиологического эксперимента, на который они опираются. Так, для описания нейронов ЦГ обычно используются варианты классической модели Ходжкина-Хаксли (1952 г.), включая ее разнообразные обобщения, учитывающие дополнительные мембранные токи, или, наоборот, более упрощенные, использующие в качестве переменных мембранный потенциал V(t) и некоторые вспомогательные токи, описывающие процессы двух типов быстрые Ie(t) и медленные I_M(t) (см., например, [13-15]).

Типичная обобщенная модель Ходжкина-Хаксли (в широком смысле conductance-based model) имеет вид

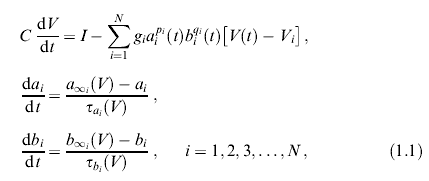
где V(t) — электрический потенциал клеточной мембраны, С характеризует электрическую емкость мембраны, iобозначает вид тока, текущего через мембрану, или, как говорят, тип ионного канала (калиевого, натриевого, кальциевого канала, канала утечки), g_i — максимальная проводимость, V_i — равновесный потенциал (потенциал реверсии) для i-го канала, a_i и b_i — переменные, характеризующие активацию и инактивацию i-го канала, эти переменные можно рассматривать, например, как вероятности открытия или закрытия того или иного канала, a p_iи q_i представляют собой число управляющих частиц, достаточное, чтобы открыть или закрыть канал (обычно это целые числа от нуля до четырех). a_∞i (V) и b_∞i(V) — стационарные состояния уровня активации и инактивации, они зависят от V сигмоидным образом, так же как и характерные времена релаксации ф_ai(V) и ф_ai(V). В классической работе Ходжкина и Хаксли [14] N = 3.

Сейчас популярны и более простые модели подобного типа. Одна из них — модель Морриса-Лекара [15]:

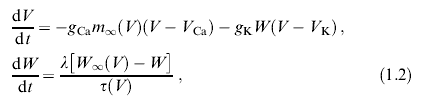
где m_∞(V), W_∞(V), ф(V) — функции сигмоидного типа. Здесь учтена всего лишь одна переменная W,описывающая активацию нейрона. Естественно, что в рамках динамической модели с двумерным фазовым пространством невозможно описать все детали динамики нейрона и, в первую очередь, хаотические колебания мембранного потенциала клетки, наблюдаемые в различных экспериментах [16, 17] (поскольку странный аттрактор не может быть вложен в двумерное пространство). Поэтому сейчас весьма широко используются трехмерные модели, также опирающиеся на формализм Ходжкина-Хаксли. Это, например, модель Чэй [18] и др.

Формализм Ходжкина и Хаксли, основанный на детальном анализе ионного транспорта через мембрану, получил широкое распространение. Но весьма продуктивны и феноменологические модели, описывающие основные особенности динамики нейронов. Одна из моделей такого типа — модель Розе-Хиндмарш [19] (более подробно см. раздел 3):

где х – мембранный потенциал, у характеризует "быстрые" токи (например, калиевые и натриевые), а z –"медленные" токи, I – внешний ток, а, Ь, с, d, r, s, х₀ – постоянные параметры.

При обсуждении динамических процессов в коре головного мозга наиболее часто используется модель нейронной активности Вилсона и Кована (1972 г.), учитывающая взаимодействие двух связанных популяций нейронов – подавляющих и возбуждающих [20]:

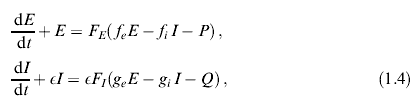
где Е и I – безразмерные величины, характеризующие активность возбуждающих и тормозящих нейронов соответственно. Здесь параметр е < 1, поскольку постоянные времени для торможения, как правило, больше характерных времен возбуждения, F – функция сигмоидного типа: F=l/(l+e^-x) или F= 1/2 + (1/р) arctanx.

При моделировании больших ансамблей нейронов часто используют и совсем простые точечные модели в виде фазовых осцилляторов, к которым сводятся системы осцилляторов общего вида с периодическим поведением и слабыми парными связями (см., например, [21], обзор [22]):

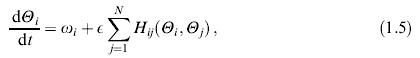
или еще более простые модели переключательного, спинового, типа, подобные тем, которые широко применяются в теории фазовых переходов.

Описанные выше модели нейронов дублируют именно физиологические и анатомические особенности отдельного нейрона. Но при создании нейронной сети нет необходимости в таком точном воспроизведении естественного нейрона. Необходим нейрон, удовлетворяющий поставленным требованиям, и не усложненный реализацией лишних в рамках поставленной задачи физиологических особенностей, так как это будет негативно отражаться на быстродействии сети. Необходима упрощенная, но подходящая для поставленной задачи распознавания модель.

В поставленной задаче необходим пороговый, импульсный нейрон, удовлетворяющий требованию пластичности и стабильности. Для решения этой задачи я взяла двухпороговый нейрон (рис. 15).

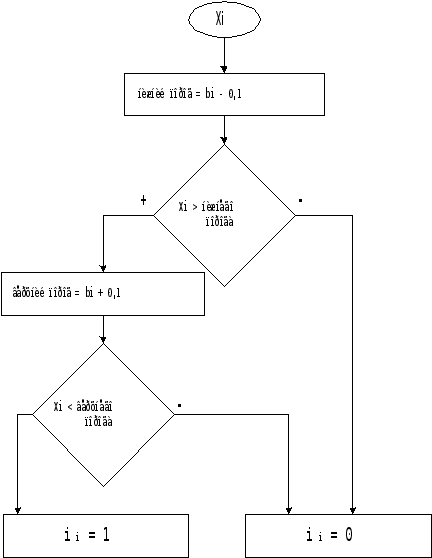
Рис.15. Двухпороговый нейрон.

При прохождении входным сигналом нижнего порога, и не превышении верхнего, нейрон срабатывает и генерирует импульс.

После обучения нейронного ансамбля, он будет узнавать только сигнал, мало отличающийся от запомненного. Т.е. ансамбль будет генерировать положительный импульс только в случае резонанса входного сигнала и сигнала, которому обучен ансамбль (рис. 16).

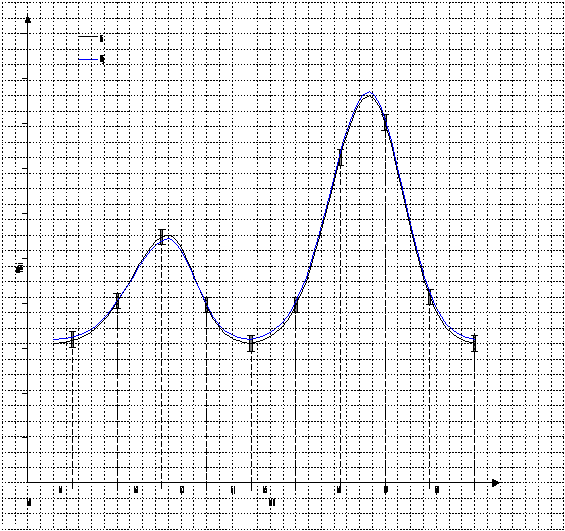
Рис.16. Резонанс.