5 Построить потенциальную диаграмму для какого-либо контура, включающего точки a и b

Потенциальная диаграмма – диаграмма распределения потенциала вдоль замкнутого контура цепи; по оси абсцисс один за другим в выбранном масштабе откладываются сопротивления контура; по оси ординат в выбранном масштабе – потенциалы всех точек схемы (после каждого элемента цепи ставится точка, потенциал которой необходимо определить).

Решение:

Е₁=25 В, Е₂=50 В, Е₃=75 В;

r₁=15 Ом, r₂=30 Ом, r₃=45 Ом, r₄=60 Ом, r₅=75 Ом;

=2 А.

Рисунок 6 – Расчетная схема

Составляем расчетную схему цепи, на которой показываем выбранные положительные направления всех токов и ЭДС, а также пронумеровываем все узлы схемы (рисунок 6).

Определяем значения потенциалов для контура 32b4a13:

(0;0)

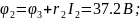(30;37.2)

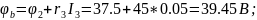(75;39.45)

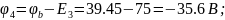(75;-35.6)

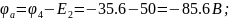(75;-85.6)

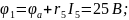(150;25)

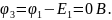(150;0)

Составляем потенциальную диаграмму для контура 32b4a13 (рисунок 7):

Рисунок 7 – Потенциальная диаграмма для контура 32b4a13

6 Определить напряжение между точками a и b

Закон Ома устанавливает связь между током I и напряжением U на сопротивлении приемника (нагрузки):

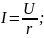
Для участка цепи с ЭДС закон Ома представляется следующим образом:

.

Решение:

Е₁=25 В, Е₂=50 В, Е₃=75 В;

r₁=15 Ом, r₂=30 Ом, r₃=45 Ом, r₄=60 Ом, r₅=75 Ом;

=2 А.

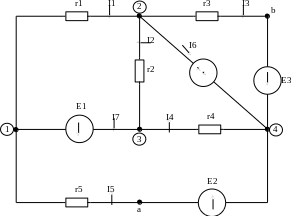
Рисунок 8 – Расчетная схема

Составляем расчетную схему цепи, на которой показываем выбранные положительные направления всех токов и ЭДС (рисунок 8).

Используя обобщенный закон Ома, определим напряжение между точками a и b:

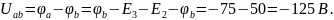
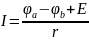16