2.2 Принцип работы и схема транзисторного амплитудного модулятора.
Н
а
практике в качестве нелинейных элементов
модуляторов чаще используются транзисторы.
Модулируемое высокочастотное напряжение
подают во
входную цепь
нелинейного элемента. Модулирующий же
сигнал вводят в цепи различных электродов:
в транзисторах - в цепь базы или коллектора
(соответственно базовая или коллекторная
модуляция). Рассмотрим схему базовой
модуляции на транзисторе (рис. 1).
Напряжение на базе содержит, кроме
смещения Еб,
определяющего положение рабочей точки,
колебания низкой и высокой частот
Рисунок 1 - схема транзисторного амплитудного модулятора
Здесь
u1
= U1
cos
ω0t—высокочастотное
напряжение; u2
= U2
cos
Ωt
— модулирующее
низкочастотное напряжение. Коллекторный
ток представляет последовательность
импульсов, отличающихся друг от друга
высотой Imax
и углом отсечки θ. Если разложить каждый
из этих импульсов тока в ряд Фурье за
период высокой частоты
,
получим постоянную составляющую и
гармоники высокой частоты.
Напряжение на контуре, настроенном на частоту ω0, создается только первой гармоникой ik1=Ik1cos ω0t: uвых=ik1Rэ=Ik1 Rэcos ω0t.
Изменение высоты и ширины импульсов тока во времени приводит к изменению амплитуды Iк1 с низкой частотой Ω. Поэтому выходное напряжение получается модулированным по амплитуде.
Режим работы модулятора, определяемый величинами Eб, U1 и U2, нельзя выбирать таким, чтобы все мгновенные значения находились в пределах линейного участка характеристики транзистора, так как в этом случае коллекторный ток будет иметь такую же форму, что и uб, амплитуда высокочастотной составляющей тока ik1 будет постоянной, а потому напряжение на выходе окажется немодулированным.
При осуществлении модуляции могут возникать искажения огибающей AM колебания. Оценка величины искажений и выбор режима работы, обеспечивающего их отсутствие, по характеристике прямой передачи ik1(uб) практически невозможны. Для решения этой задачи целесообразен иной подход к рассмотрению работы модулятора. Напряжение uб можно рассматривать как сумму высокочастотного колебания u1 и напряжения смещения uб(t)= Eб+ u2(t), медленно изменяющегося с низкой частотой, а модуляцию как следствие изменения смещения, приводящего к изменению импульсов тока и их первой гармоники. Так как амплитуда выходного напряжения пропорциональна Iк1, для получения неискаженной модуляции требуется, чтобы амплитуда Iк1 изменялась пропорционально изменению напряжения смещения.
Под СМХ понимается зависимость амплитуды первой гармоники тока коллектора Ik1 транзистора от постоянного напряжения смещения на базе Uбэ, при постоянной амплитуде напряжения несущей коллектора.
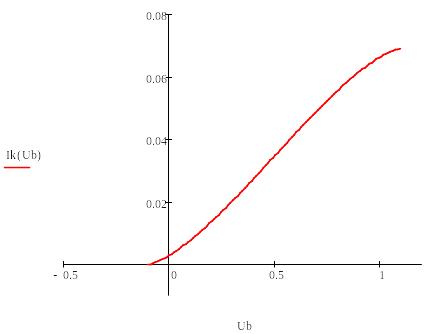
Необходимо определить с помощью СМХ оптимальное напряжение смещения и допустимую величину амплитуды модулирующего сигнала.
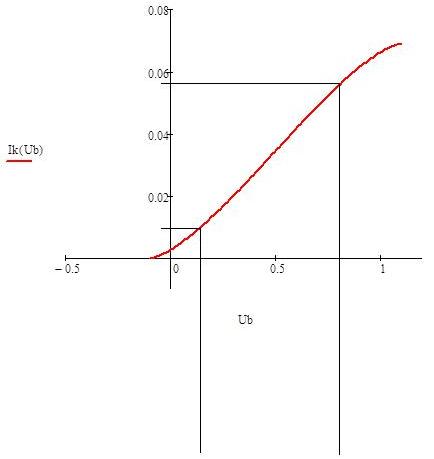
Оптимальное смещение находится на середине этого линейного участка.
Определим коэффициент амплитудной модуляции:
Запишем математическое выражение этого сигнала по следующим данным.
Umax=0,33 В
М=1
f0=650 кГц
F=5 кГц
с-1
с-1
Задача №3
Вольт-амперная характеристика (ВАХ) диода линейного диодного детектора аппроксимирована отрезками двух прямых линий
Требуется:
а) пояснить назначение детектирования модулированных колебаний.
б) изобразить схему линейного диодного детектора, описать принцип его работы и назначение элементов, входящих в схему детектора;
в) рассчитать сопротивление нагрузки RH для получения заданного коэффициента детектирования Kд
г) выбрать значение ёмкости нагрузки детектора СН при заданных f0 и F.
д) рассчитать и построить спектры напряжений на входе и выходе детектора.
Исходные данные:
На входе детектора воздействует амплитудно-модулированное колебание:
S=45 мА/В
MAM=0.9
КД=0.65
Um=1.4 B
f0 =550 кГц
F=4.5 кГц
3.1 Детектированием (демодуляцией) – называется процесс преобразования модулированного высокочастотного сигнала в колебание, форма которого воспроизводит низкочастотный модулирующий сигнал. Детекторы (демодуляторы) выполняют функцию, обратную функции, осуществляемой модуляторами и подразделяются на амплитудные, частотные, фазовые, импульсные, цифровые и т.д. Детектирование модулированных колебаний, принятых по каналу связи, существует для получения исходного информационного сигнала.
3.2 Схема диодного детектора изображена на рисунке (особенно пригодная для работы с сигналами большого уровня). Такой детектор образован последовательным соединением диода и параллельной RC-цепи, которая выполняет роль частотного фильтра. Для нормального функционирования схемы необходимо, чтобы сопротивление нагрузки Rн значительно превышало сопротивление диода в прямом направлении, т.е. чтобы SRн>>1. При подаче на вход детектора АМ-колебания конденсатор заряжается через открытый диод значительно быстрее, чем разряжается через резистор, поэтому выходное напряжение примерно повторяет огибающую входного напряжения. Диод большую часть периода входного колебания закрыт и амплитуда выходного напряжения близка к амплитуде входного.
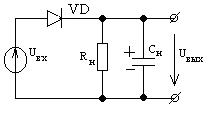
Схема диодного детектора
3.3 Рассчитаем сопротивление нагрузки RH для получения заданного коэффициента детектирования Kд.
Коэффициент передачи детектора Кд равен:
где θ – угол отсечки входного сигнала. Он находится из соотношения:
Отсюда θ = arcos Кд = arcos(0,8)=0,863рад
3.4 Выбираем значение ёмкости нагрузки детектора СН при заданных f0 и F.
Чтобы нагрузка выполняла роль частотного фильтра, подавляющего высокочастотные спектральные составляющие, необходимо:
Преобразуем выражение:
Следовательно,
где
Сигнал на входе детектора выглядит следующим образом:
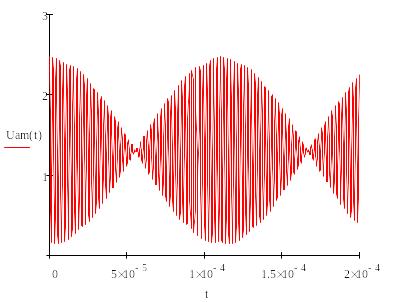
3.5 Строим спектры напряжений на входе и выходе детектора
Спектр напряжения на выходе
Спектр напряжений на входе
Задача №4
Задана кодовая комбинация простого первичного кода Q(0,1)
Требуется:
а) закодировать ее помехоустойчивым циклическим кодом, исправляющим однократную ошибку (tиспр.=1);
б) проверить правильность построения кодовой комбинации циклического кода F(0,1);
в) составить таблицу синдромов циклического кода;
г) проверить, будет ли исправлена однократная ошибка в i – м разряде кодовой комбинации циклического кода;
д) построить структурную схему кодера циклического кода.
Исходные данные:
Последняя цифра зачетной книжки 2 = 10
Предпоследняя цифра зачетной книжки 4 = 11
K=1011
i = 3
Кодовая комбинация: 1011 (к=4)
а) Чтобы код позволял исправлять tиспр-кратные ошибки, необходимо минимальное кодовое расстояние:
d0=2∙tиспр+1=2∙1+1=3
Для кода с d0=3 известно точное соотношение для определения числа проверочных элементов:
где k – число информационных элементов.
В нашем случае k=4, минимальное удовлетворяющее условию значение r=3, общая длина кодовой комбинации:
б) Разрешенные кодовые комбинации циклического кода делятся без остатка на образующий полином. Степень образующего полинома равна количеству проверочных элементов. Выберем образующий полином:
Разрешенную кодовую комбинацию можно вычислить по формуле в алгебраическом виде:
где Q(x) – кодовая комбинация простого кода,
R(x)
– остаток от деления
Кодовая комбинация простого кода в алгебраическом и цифровом виде:
Вычислим кодовую комбинацию циклического кода.
В алгебраическом виде:
x6+x4+ x3 x6+x4+ x3 000 |
x3+x+1 |
x3+ x2 |
В цифровом виде:
Проверим правильность составления кодовой комбинации, для этого поделим её на образующий полином, если получим нулевой остаток, значит кодовая комбинация составлена правильно.
x6+x4+ x3 x6+x4+ x3 0 |
x3+x1+1 |
x3 |
|
|
|
|
|
|
Следовательно, данная кодовая комбинация построена правильно.
в) Построим производящую матрицу циклического кода
Возьмем следующие комбинации(содержащие единицу в одном разряде):
Q(0,1): Q1=1000; Q2=0100; Q3=0010; Q4=0001
Найдём первую строку производящей матрицы:
F1(x)=Q1(x)∙x3/G(x)=x6/x3+x1+1=1000 101
Аналогично:
F2(0,1)= 0100 111
F3(0,1)= 0010 110
F4(0,1)=0001 011
Производная матрица G7,4 имеет вид:
G7,4= |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
|
0 |
0 |
1 |
0 |
1 |
1 |
0 |
|
0 |
0 |
0 |
1 |
0 |
1 |
1 |
Проверочная матрица H7,4 имеет вид:
H7,4= |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
0 |
0 |
0 |
1 |
Составим таблицу синдромов циклического кода.
С3,4= |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
2 |
|
1 |
1 |
0 |
3 |
|
0 |
1 |
1 |
4 |
|
1 |
0 |
0 |
5 |
|
0 |
1 |
0 |
6 |
|
0 |
0 |
1 |
7 |
г) Проверим, будет ли исправлена ошибка в i-том разряде кодовой комбинации циклического кода. i=3
F’(0,1)=1001000
x6+x3 x6+x4+ x3 x4 x4+ x2+x x2+x |
x3+x1+1 |
x3+x |
|
|
|
|
|
|
110→ошибка в 3-eм символе.
Ошибка исправлена
д) На рисунке 1 представлена схема кодера. Следует иметь в виду, что число ячеек сдвигающего регистра и регистра задержки выбирается равным степени образующего полинома, а число сумматоров – на единицу меньше веса образующего полинома. Сумматоры по модулю два включаются перед ячейками, которые стоят на позициях единиц в образующем полиноме, за исключением старшего разряда.
Образующий полином P(x)=x3+x2+1, что соответствует P(0,1)=1101, тогда регистр сдвига должен иметь 3 ячейки (образующий полином 3-й степени), в него включаются два сумматора, которые включаются перед первой и третьей ячейками.
Рисунок 1 – Схема кодера
Режим работы.
Такая схема содержит регистр задержки (РЗ), обеспечивающий сдвиг информационной группы на четыре такта, и формирователь проверочной группы, включающий регистры сдвига и сумматоры по модулю 2 в цепи обратной связи. В схеме также имеются два ключа К1 и К2, обеспечивающие необходимую последовательность функционирования. В положении, когда К1 замкнут, а К2 разомкнут, информационная часть кода подается на вход схемы, т. е. в первую ячейку регистра задержки, и через S1 в первую ячейку сдвига. По окончании четырех тактов старший разряд информационной группы записывается в последние ячейки обоих регистров. Во время пятого такта информационная группа начинает поступать на выход схемы. С этого момента К1 размыкается, а К2 замыкается. . Начиная с пятого такта формирователь проверочной группы будет функционировать в соответствии с ранее описанной процедурой. После девятого такта К2 размыкается, а К1 замыкается. С этого момента формирователь проверочной группы работает как обычный регистр сдвига, выталкивая на выход записанные в ячейках кодовые импульсы проверочной группы. Одновременно в регистры начинает поступать новая группа информационных элементов.
Число ячеек сдвигающего регистра и регистра задержки выбирается равным степени образующего полинома, а число сумматоров – на единицу меньше веса образующего полинома. Сумматоры по модулю два включаются перед ячейками, которые стоят на позициях единиц в образующем полиноме, за исключением старшего разряда. Образующий полином P(x)=x3+x2+1, что соответствует P(0,1)=1101, тогда регистр сдвига должен иметь 3 ячейки (образующий полином 3-й степени), в него включаются два сумматора, которые включаются перед первой и третьей ячейками.