Обробка результатів вимірювань

Результат вимірювання, під яким розуміють значення величини, певне при її вимірюванні, одержують після відповідної обробки результатів спостережень: визначають систематичну складову погрішності й виключають промахи. Систематичну складову виключають шляхом введення виправлення П. Значення виправлення дорівнює абсолютної систематичної погрішності , узятої із протилежним знаком:

З урахуванням виправлення результат вимірювання приймає значення

Вплив випадкової складової погрішності можна зменшити багаторазовим повторенням того самого вимірювання в однакових умовах (з наступною обробкою результату методами математичної статистики). Тому що ймовірність появи позитивних і негативних випадкових погрішностей однакова, то за результат вимірів при досить великій їхній кількості приймають середнє арифметичне х_СР із всіх отриманих результатів х₁, х₂, х₃... х_n:

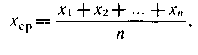
де п — кількість вимірювань.

Випадкову погрішність одиничного вимірювання характеризують середньоквадратичною погрішністю (, що дорівнює

При цьому максимальна випадкова погрішність М дорівнює

З урахуванням систематичної й випадкової складових погрішності границі можливих значень вимірюваної величини визначаються наступними вираженнями:

— з імовірністю 95 %,

— з імовірністю 99,7%.

При обробці результатів непрямих вимірювань, якщо шукана вимірювана величина х дорівнює добутку декількох величин, обмірюваних прямим методом:

де к, т, п — постійні числа, те гранична відносна погрішність непрямого вимірювання визначається наступним вираженням:

Наприклад, при визначенні потужності по відомій формулі

відносна погрішність дорівнює:

При обробці непрямих вимірювань, якщо вимірювана величина X дорівнює сумі (різниці) декількох однорідних величин X = Х₁ ± Х₂ ±:..., гранична відносна погрішність визначається вираженням

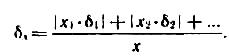
У результаті обробки результатів спостережень одержуємо числове значення вимірюваної шуканої величини. Отримане значення погрішності виміру дозволяє оцінити числові значення, які є достовірними.

Існують наступні правила округлення результатів обробки:

1. У значенні погрішності втримується не більше двох значущих цифр, причому остання цифра округляється звичайно до нуля або п'яти.

2. Числове значення результату вимірювань повинне кінчатися цифрою того ж розряду, що й значення погрішності. Приклад: 235,732±0,15 округляється до 235,73 + 0,15.

3. Якщо перша із цифр, що відкидаються, менше п'яти, то цифри, що залишаються, не змінюються. Приклад: 442,741 ±0,4 округляється до 442,7 ±0,4.

4. Якщо перша із цифр, що відкидаються, більше або дорівнює п'яти й за нею треба значуща цифра, то остання цифра, що залишається, збільшується на одиницю. Приклад: 37,268±0,5 округляється до 37,3 ±0,5; 37,252 ±0,5 округляється до 37,3±0,5.

5. Якщо перша із цифр, що відкидаються, дорівнює п'яти й за нею не треба значущих цифр, то округлення здійснюється до найближчого парного. Приклад: 21,35±0,2 округляється до 21,4 ±0,2; 21,45±0,2 округляється до 21,4 ±0,2; 21,55±0,2

. округляється до 21,6 ±0,2.

Останнє правило утрудняє обробку результатів вимірювань за допомогою ЕОМ. У зв'язку із цим, якщо перша із цифр, що відкидаються, дорівнює п'яти, пропонується збільшувати останню із цифр, що залишилися, на одиницю.