9.Тіла обертання
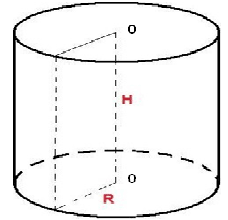
Циліндр - тіло, утворене обертанням прямокутника навколо його сторони.
|
S = Sбіч + 2Sосн Sбіч = 2πRH Sосн = πR2 S = 2πR(R + H) V = SбічH = πR2H |
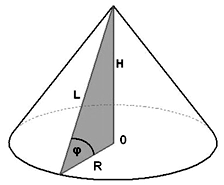
Конус – тіло, утворене обертанням прямокутного трикутника навколо одного із його катетів.
|
S = Sбіч + Sосн Sбіч = πRL Sосн = πR2 S = πR(R + L) Sосн = Sбіч•cos φ V = 1/3•Sосн•H = 1/3•πR2H |
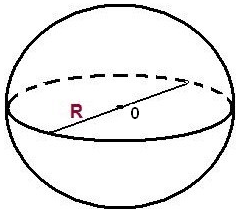
Куля – тіло, утворене обертанням круга навколо його діаметра.
|
Поверхня кулі - сфера. S = 4πR2 V = 4/3•πR3 |
10.Координати і вектори в просторі
|
Прямокутна (декартова) система координат в просторі задається трійкою попарно перпендикулярних осей. Відстань між двома точками A(XA; YA; ZA) i B(XB; YB; ZB) в просторі визначається формулою:
Якщо С(XС; YС; ZС) – середина відрізка AB, то
|
Якщо
вектор a, який знаходиться в прямокутній
системі координат OXYZ, має початком точку
A з координатами XA,
YA,
ZA,
а кінцем – точку B з координатами XB,
YB,
ZB,
то числа XB -
XA,
YB -
YA,
ZB -
ZA називається
його координатами: a( XB -
XA;
YB -
YA;
ZB -
ZA).
Довжина
(модуль) цього вектора:
Сумою векторів a(XA; YA; ZA) і b(XB; YB; ZB) називається вектор c(XA + XB; YA + YB; ZA + ZB).
Добутком вектора a(XA; YA; ZA) на число λ називається вектор λa(λXA; λYA; λZA).
Скалярним добутком векторів a та b, якщо відомі їх координати, є величина a•a = XA•XB + YA•YB + ZA•ZB.
Для кута φ між векторами a та b:
