7.Прямі та площини в просторі

Аксіоми про властивості площини

• Через будь-які три точки, що не належать одній прямій, можна провести одну і тільки одну площину.

• Дві площини, що мають спільну точку, перетинаються по прямій, яка містить цю точку.

• Якщо площині належать дві точки прямої, то і уся пряма належить цій площині.

Висновки аксіом

1. Одну і тільки одну площину можна провести через:

   • пряму і точку, що не належить цій прямій;

   • дві перетинні прямі;

   • дві паралельні прямі.

2. Пряма в просторі може належати безкінечній множині площин.

Якщо площина і пряма, що не лежить у ній, перпендикулярні до однієї і тієї самої прямої, то вони паралельні.

Пряма, паралельна деякій прямій, що лежить у площині, паралельна і самій площині.

Дві площини, що містять паралельні прямі, перетинаються по прямій, паралельній даним.

Площина, що містить деяку пряму, паралельну іншій площині, перетинає останню по прямій, паралельній даній.

Якщо одна з двох паралельних прямих паралельна деякій площині, то і інша пряма паралельна цій площині або належить їй.

Пряма перпендикулярна до площини , якщо вона перпендикулярна до будь-якої прямої, що лежить у цій площині.

Пряма перпендикулярна до площини , якщо вона перпендикулярна до двох прямих, що перетинаються і лежать у цій площині.

Паралельними є площини, які не мають спільних точок. Якщо ж площини мають спільну пряму, то їх називають перетинними.

Дві площини є паралельними, якщо одна з них паралельна двом перетинним прямим, що лежать у іншій площині.

Якщо паралельні площини перетинаються третьою, то лінії їх перетину паралельні між собою.

Пряма, що лежить в одній із перпендикулярних площин і перпендикулярна до лінії їх перетину, перпендикулярна до іншої площини.

Якщо площина перпендикулярна до двох перетинних площин, то вона перпендикулярна до ребра, утвореного ними двогранного кута.

Якщо площина перпендикулярна до ребра двогранного кута, то вона перпендикулярна і до площин, що його утворили.

Прямі називаються паралельними, якщо вони лежать у одній площині і не мають спільних точок. Кут між паралельними прямими дорівнює 0°.

Якщо ж у прямих є спільна точка, то вони називаються перетинними. Кутом між перетинними прямими називається менший із кутів, які утворюються при перетиканні прямих.

Якщо прямі не лежать в одній площині і не мають спільних точок, то їх називають мимобіжними. Через кожну з мимобіжних прямих можна провести одну і тільки одну площину, паралельну іншій прямій. Кутом між мимобіжними прямими називається кут між прямими, які перетинаються і паралельні даним мимобіжним прямим.

8.Многогранники

Позначення:

S - площа поверхні; S_біч. - площа бічної поверхні; S_осн. - площа основи; P_осн. - периметр основи; P_┴ - периметр перпендикулярного перерізу; S_┴ - площа перпендикулярного перерізу; L - довжина бічного ребра (твірної); H - висота; V - об’єм.

Призма

Призма – многогранник, дві паралельні грані (основи) якого рівні n - кутники, а інші n граней (бічні грані) – паралелограми.

S = S_біч. + 2S_осн.; V = S_осн.•H; S_біч. = P_┴•L; V = S_┴•L.

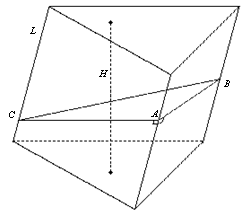
На рисунку зображено трикутну призму, в якій трикутник ABC – перпендикулярний переріз.

Призма, в якій бічні ребра перпендикулярні до основи, називається прямою. Для прямої призми S_біч. = P_осн.•H.  Пряма призма, в основі якої лежить правильний многокутник, називається правильною.

Призма, в основі якої лежить паралелограм, називається паралелепіпедом. Прямий паралелепіпед, в основі якого лежить прямокутник, називається прямокутним паралелепіпедом. Його об’єм V = a•b•c, де a, b, c - виміри паралелепіпеда. Для куба, у якого a = b = c, V = a³, S = 6a² .

Піраміда

Піраміда – многогранник, одна грань (основа) якого n - кутник, а інші n граней (бічні грані) – трикутники, що мають спільну вершину. Для піраміди

S = S_біч. + S_осн.; V = (1/3)•S_осн.•H.

Піраміда, в основі якої лежить правильний многокутник, центр якого збігається з основою висоти піраміди, називається правильною. Висота бічної грані правильної піраміди, проведеної із вершини піраміди, називається її апофемою (l).

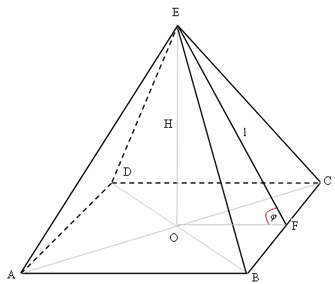
На рисунку зображено правильну чотирикутну піраміду, у якої EF = l - апофема,  OE = H - висота,  кут EFO = φ - кут між бічною гранню BEC і основою ABCD. Для правильної піраміди: Sосн. = Sбіч.•cos φ; Sбіч. = (1/2)•Pосн.•l.