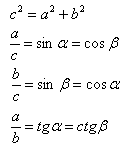19.Елементи комбінаторики

Комбінаторика вивчає питання про те, скільки різних комбінацій, підпорядкованих тим чи іншим умовам, можна скласти із заданих об’єктів.

Розміщенням із n елементів по m називається любий впорядкований набір із m різних елементів, вибраних із загальної сукупності в nелементів.

При цьому можуть бути розміщення без повторень

, коли два набори вважаються різними,

якщо вони відрізняються один від одного хоча б одним елементом, або коли набори однакові по складу, - порядком розташування цих елементів в наборі.

В цьому випадку справедливе співвідношення

де n! = 1•2•3•...•n, (n - m)! = 1•2•3•...•(n - m).

В розміщеннях з повтореннями

в набір можуть входити і однакові елементи,

але набори також відрізняються один від одного або складом елементів, або порядком розміщення цих елементів в них.

Доведено, що

Перестановками із n елементів називається любий впорядкований набір цих елементів.

В перестановках без повторень

набори містять n елементів із n і відрізняються

один від одного лише порядком елементів в них.

Очевидно, що

Комбінацією із n елементів по m називається любий невпорядкований набір із m різних елементів, вибраних із загальної сукупності в nелементів.

В комбінаціях без повторень

набори відрізняються один від одного лише складом

і розраховуються по формулі

Із приведених визначень видно, що результати підрахунків залежать від декількох факторів одночасно. По-перше, від того, із якої кількості елементів можна складати набори. По-друге, результат залежить від того, якої величини набори елементів потрібні. Важливо також знати, чи являється суттєвий порядок елементів в наборі. Якщо в умовах задачі є якісь особливості, то вони розв’язуються в першу чергу.

В попередні роки тести по математиці містили завдання по комбінаториці, для розв`язання яких не обов`язково використовувати формули, а достатньо було керуватися лишь логічними міркуваннями. Такого ж типу завдання по комбінаториці включені і в тести даної частини.

20.Початки теорії імовірностей

Імовірність події А дорівнює відношенню числа випробувань m, що сприяють появі події A, до числа всіх можливих результатів випробування n:

Властивості імовірності

1. Для кожної події А, 0 ≥ P(A) ≥ 1

2. Для вірогідної події Ω, P(Ω) = 1

3. Якщо A = B + C, причому B і C несумісні, то P(A) = P(B) + P(C)

21.Елементи статистики

4. Задача математичної статистики полягає в систематизації, обробці й використанні статистичних даних.

5. Статистичні дані представляють у вигляді таблиці або полігона частот.

6. На осі X відкладають значення признаку (варіанти) X_j , на осі n – відповідні значення частот n_j.

Модою Mo називають варіанту, яка має найбільшу частоту. Медіаною Me називають варіанту, яка ділить варіаційний ряд пополам. Розмахом варіювання називають різницю між найбільшою і найменшою варіантами. Середнім значенням н азивають величину:

1.Геометричні фігури на площині

Геометричною фігурою називають будь-яке утворення з точок:

- відрізок,

- розгорнутий кут.

За одиницю вимірювання кутів прийнято градус (1°), який дорівнює 1/180 частині розгорнутого кута. Меншими одиницями вимірювання є мінута (') і секунда ('') - 1° = 60', 1' = 60''.

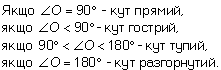
Бісектриса кута OC це промінь, який ділить його навпіл:

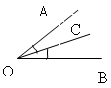
Крім градусної міри існує радіанна міра вимірювання кутів. Її одиницею є кут 1 радіан – це центральний кут з вершиною в центрі кола радіуса R, що опирається на дугу довжиною R. Співвідношення між градусами і радіанами приводиться в таблиці

Градуси	0°	30°	45°	60°	90°	180°	270°	360°
Радіани	0	n/6	n/4	n/3	n/2	n	3n/2	2n

Дві прямі на площині називаються паралельними, якщо вони не перетинаються. Якщо дві паралельні прямі перетнуті третьою прямою, то:

Дві прямі, паралельні третій, паралельні між собою. Якщо дві прямі перетинаються під прямим кутом, то їх називають перпендикулярними. Через кожну точку прямої можна провести перпендикулярну до неї пряму і тільки одну. Через дану точку поза прямою можна провести пряму, перпендикулярну до даної прямої, і тільки одну.

2. Трикутники

В ластивості трикутника:

Види трикутників:

1. За довжиною сторін: різносторонні, рівнобедрені, рівносторонні (правильні);

2. За величиною кута: гострокутні, тупокутні, прямокутні.

Основні лінії в трикутнику:

1. Висота (h) – перпендикуляр з вершини кута на протилежну сторону;

2. Медіана (m) – відрізок, що сполучає вершину із серединою протилежної сторони;

3. Бісектриса (ℓ) – відрізок, що ділить кут пополам.

	У рівнобедреному трикутнику b - основа трикутника, a = c;
	У рівносторонньому трикутнику a = b = c,
	У прямокутному трикутнику ﮮ ɣ = 90º, a i b - катети, c - гіпотенуза Теорема Піфагора:

Площа трикутника:

Співвідношення між елементами трикутника:

Теорема косинусів:

Теорема синусів: