
Экзамен / Шпоры по математике / shpora_ryady_i_difury
.doc
|
1. Предел числовой последовательности и его свойства. Арифметические действия с пределами. Опр1: Совокупность значений ф-и an=f(n) натурального аргумента n наз-ся числовой последовательностью и обозначается а1,а2,..аn или кратко { аn } Опр2: Число А наз-ся пределом последовательности { аn }, если для любого сколь угодно малого ε>0 существует такое число N, что для всех номеров n>N выполняется условие | аn-A|< ε Арифметические действия: Если последовательности { аn } и { bn } имеют предел, то имеют предел следующие последовательности:{ аn + bn },{ аn - bn },{ аn * bn }, { аn / bn } при условии bn≠0. Причем
Док-во 1)
Согласно опр это означает, что
|
2. Числовой ряд. Сходимость ряда. Сумма ряда. Остаточный член ряда. Необходимый и достаточный признак сходимости ряда. Сложение и умножение на число сходящихся рядов.
Числовой
ряд.
Рассмотрим произвольную числовую
последовательность
Сходимость
числового ряда.
Ряд
Суммирование числовых рядов. Если возможно найти общий член последовательности an, то по определению можно найти и сумму ряда, вычисляя предел этой последовательности.
|
3. Числовой ряд. Сходимость ряда. Необходимый признак сходимости ряда. Примеры.
Числовой
ряд.
Рассмотрим произвольную числовую
последовательность
Сходимость
числового ряда.
Ряд
.
Если ряд сходится, то предел общего
члена равен 0
Док-во:
Т.к. ряд сходится, то сущ пределы
Пример
|
|
4. Признаки сравнения для рядов с положительными членами.
1.
Рассмотрим два числовых ряда с
неотрицательными членами
2.
Если для таких же двух рядов существует
конечный отличный от 0 предел отношений
общих членов данных рядов
(Т.к. это геом прогрессия, то сумма Sn при |q|≠1
7. Знакопеременные ряды. Абсолютная сходимость. Условная сходимость. Примеры. Действия с абсолютно сходящимися рядами.
Абсолютная и условная сходимость. Опр:
Ряд
Опр:
Ряд
Действия с абсолютно сходящимися рядами: 1)Если ряд абс сходится и имеет сумму S, то ряд, полученный из него перестановкой членов, также сходится и имеет ту же сумму S. 2) Абс сходящиеся ряды с суммами S1 и S2 можно почленно складывать(вычитать), в результате чего получается абс сходящийся ряд,сумма которого S1 + S2 (S1 - S2) 3)Под произведением 2 рядов a1+ a2+.. + an и b2+ b1+..+ bn понимают ряд вида (a1b1)+( a1b2+ a2b1)+( a1b3+ a2b2+ a3b1)+…+( a1bn+ a2bn-1+…+ anb1)+… Произведение 2 абс сходящихся рядов с суммами S1 и S2 есть абс сходящийся ряд с суммой S1 * S2
|
5. Признаки Даламбера и Коши.
Признак
сходимости Даламбера.
Пусть члены ряда
2) при ρ>1 расходится 3) при ρ=1 нужны доп исследования Док-во 1) пусть ρ<1, то существует q такое что ρ<q<1 Т.к.
сущ
В
частности
С
некоторого номера n>N
члены данного ряда меньше членов сход
геом прогрессии Следовательно на основании 1го признака сравнения, исслед ряд сходится. 2) пусть ρ>1. Это означает, что, начиная с некоторого номера будет спроаведливо нер-во
3) ρ=1 возможны случаи сходимости и расходимости: а)
рассм сход ряд
тогда
б)
рассм расход ряд
Радикальный признак сходимости Коши. Пусть члены
ряда
1) при ρ<1 ряд сходится 2) при ρ>1 расходится 3) при ρ=1 нужны доп исследования Док-во 1)пусть
ρ<1. Возьмем q
удовл нер-ву ρ<q<1.
Т.к.
Это
нер-во показывает, что члены данного
ряда, начиная с некоторого меньше
соответствующих членов сходящейся
геом прогрессии
2)
пусть ρ>1. Это означает, что, начиная
с некоторого номера, будет справедливо
нер-во
Интегральный признак Коши. Пусть
имеется ряд Тогда
для сходимости исходного ряда необходимо
и достаточно, чтобы сходился интеграл
Замечание:
функция может быть задана на промежутке
[с,∞], тогда необходимо рассматривать
интеграл
Доказательство:
рассмотрим ряд (2)
Если (2) сходится, то из правой части неравенств по 1 признаку сравнения мы получаем, что исходный ряд сходится. Если (2) расходится, то из левой части неравенств по 1 признаку сравнения мы получаем, что исходный ряд расходится.
8. Знакочередующийся ряд. Теорема Лейбница. Оценка остатка ряда.
Ряд
Теорема Лейбница Если
все члены знакочеред ряда
в которой все положительные числа Un монотонно убывают по абсолют величине U1≥ U2≥ U3≥.. Un≥.. и
если
Док-во Докажем что сущ предел последовательности «четных» частичных сумм S2n ряда при n→∞
=> S2n монотонно возрастает с ростом n, кроме того
Независимость от «четности» или «нечетности» частичной суммы Sn при n→∞ предел существует и равен S => ряд сходится. Чтд. Оценка остатка ряда
Вывод: при замене суммы знакочередующегося ряда суммой первых его n-членов получается ошибка, модуль которой не превосходит абс величины первого отброшенного члена ряда.
|
6. Интегральных признак Коши. Его применение.
Интегральный признак Коши. Пусть
имеется ряд
Тогда
для сходимости исходного ряда необходимо
и достаточно, чтобы сходился интеграл
Замечание:
функция может быть задана на промежутке
[с,∞], тогда необходимо рассматривать
интеграл
Доказательство:
рассмотрим ряд (2)
Если (2) расходится, то из левой части неравенств по 1 признаку сравнения мы получаем, что исходный ряд расходится. Применим это признак а обобщенному гарм ряду
рассмотрим гарм ряд (р=1)
ряд расходится при р=1
9. Функциональный ряд. Область сходимости. Равномерная сходимость. Признак Вейерштрасса.
Функциональный
ряд, его сходимость. Рассмотрим ряд,
Равномерная
сходимость функционального ряда.
Пусть
Признак
Вейерштрасса
равномерной сходимости функционального
ряда: Если члены функционального рада
для
всех
|
|
10. Степенной ряд. Теорема Абеля. Область сходимости. Равномерная сходимость. Функциональный
ряд вида (1)
(1) сходится при х=0. Т.Абеля: 1)Пусть
(1) сходится абс при
Док-во:
1)Пусть (1) сходится при
=>
последовательность
Пусть
2)Пусть
(1) в точке
Предположим
противное: (1) сходится в
Степенной ряд сходится на интервале (-R;R) с центром в точке. Число R- радиус сходимости степенного ряда может быть вычислено по формулам
|
11. Непрерывность суммы степенного ряда. Интегрирование и дифференцирование степенного ряда. Рассмотрим
степенной ряд
1).S(x)
непрерывная функция в любом замкнутом
промежутке, принадлежащем интервалу
2) ряд (1) можно дифференцировать почленно внутри интервала сходимости, при этом радиус сходимости не изменяется
3) ряд (1) можно
интегрировать почленно по любому
промежутку (a,b),
лежащему в интервале сходимости, при
этом радиус сходимости полученного
ряда остается прежним.
13. Ряд Тейлора. Достаточное условие разложения в ряд Тейлора. Примеры разложения основных функций в ряд Тейлора. .
Пусть функция f(x)
определена в некоторой окрестности
точки x0
и имеет в этой точке производные всех
порядков. Ряд
называется рядом Тейлора для функции f(x) в точке x0. При x0 =0 такой ряд называют также рядом Маклорена. Функция f(x) может быть разложена в степенной ряд на интервале, если существует степенной ряд, сходящийся к f(x) на этом интервале. Если функция раскладывается в степенной ряд в некоторой окрестности точки x0, то это ряд Тейлора. Дост. условие разложимости: Если производные всех порядков ф-и f(x) ограничены в некоторой окрестности точки x=x0 одним и тем же числом M>0, то ф-я f(x) разложима в этой окрестности в ряд Тейлора. Док-во
Требуется
доказать рав-во
По
условию теоремы для
ряд сходится => Rn(x)→0 чтд Разложение основных элементарных функций
|
12. Ряд Тейлора. Разложение функции в ряд Тейлора. Необходимое и достаточное условие разложения в ряд Тейлора. Примеры разложения основных функций в ряд Тейлора.
Разложение
функций в ряд Тейлора. При исследовании
свойств бесконечно дифференцируемых
функций изучают их степенные ряды
ряды Тейлора. Пусть функция f(x)
определена в некоторой окрестности
точки x0
и имеет в этой точке производные всех
порядков. Ряд
называется рядом Тейлора для функции f(x) в точке x0. При x0 =0 такой ряд называют также рядом Маклорена. Функция f(x) может быть разложена в степенной ряд на интервале, если существует степенной ряд, сходящийся к f(x) на этом интервале. Если функция раскладывается в степенной ряд в некоторой окрестности точки x0, то это ряд Тейлора. Необх.и
дост. условие разложимости:
если ф-я разложима в ряд Тейлора в
окрестности U(х0,)
необх. и дост., чтобы Дост. условие разложимости: Если производные всех порядков ф-и f(x) ограничены в некоторой окрестности точки x=x0 одним и тем же числом M>0, то ф-я f(x) разложима в этой окрестности в ряд Тейлора.
то
Разложение основных элементарных функций
|

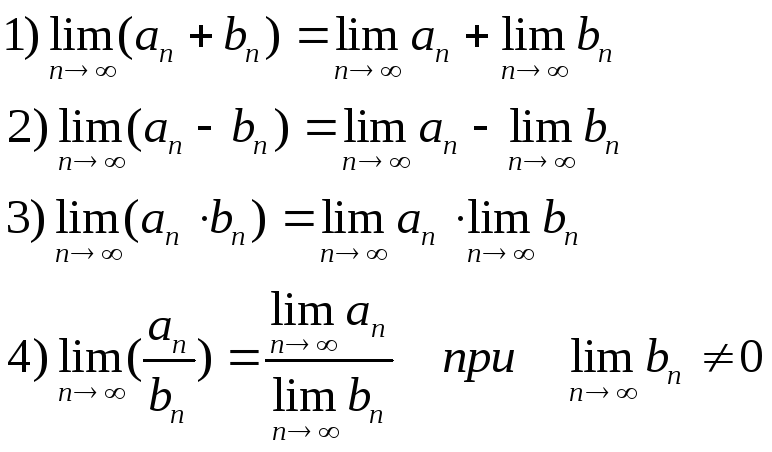

 расходится
расходится

 Из
свойств f(x)
можно написать:
Из
свойств f(x)
можно написать:
 =>
все частичные суммы S2n
ограничены числом U1,
т.е. S2n
≤ U1.
Т.к. последовательность «четных»
частичных сумм монотонна и ограничена,
то она имеет предел
=>
все частичные суммы S2n
ограничены числом U1,
т.е. S2n
≤ U1.
Т.к. последовательность «четных»
частичных сумм монотонна и ограничена,
то она имеет предел
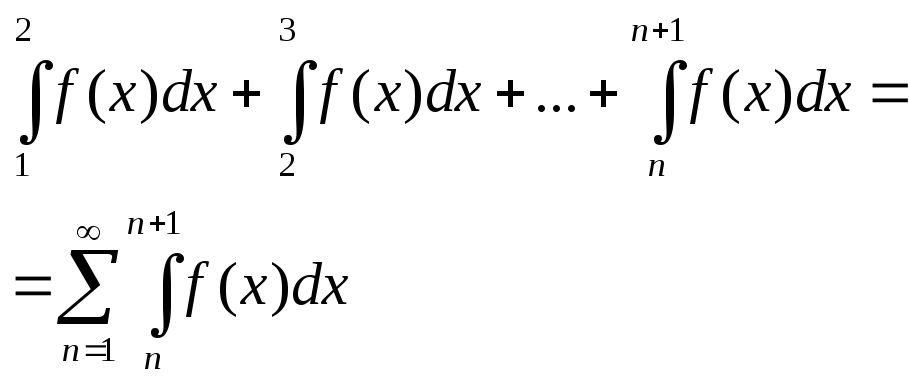 Из
свойств f(x)
можно написать:
Из
свойств f(x)
можно написать: Если
(2) сходится, то из правой части неравенств
по 1 признаку сравнения мы получаем,
что исходный ряд сходится.
Если
(2) сходится, то из правой части неравенств
по 1 признаку сравнения мы получаем,
что исходный ряд сходится.








