1.8Повторные независимые испытания

В этой теме рассматривается ситуация, когда некоторое испытание производится несколько раз: например, подбрасывается монета, или производятся выстрелы по мишени, и т.д. Один исход испытания выделен и назван успехом. В этой схеме, называемой схемой Бернулли, выделяются следующие параметры:

n – число испытаний;

p – вероятность успеха в одном испытании;

q = 1 – p – вероятность неуспеха в одном испытании.

Число успехов в п испытаниях может принимать значения от 0 до п. Это число обозначим µ_n. Нас интересует вероятность того, что µ_n примет заданное значение m, то есть Р(µ_n = m). Эту вероятность можно обозначить Р_n(m).

8. 1.8.1 (формула Бернулли). Р_n(m) = .

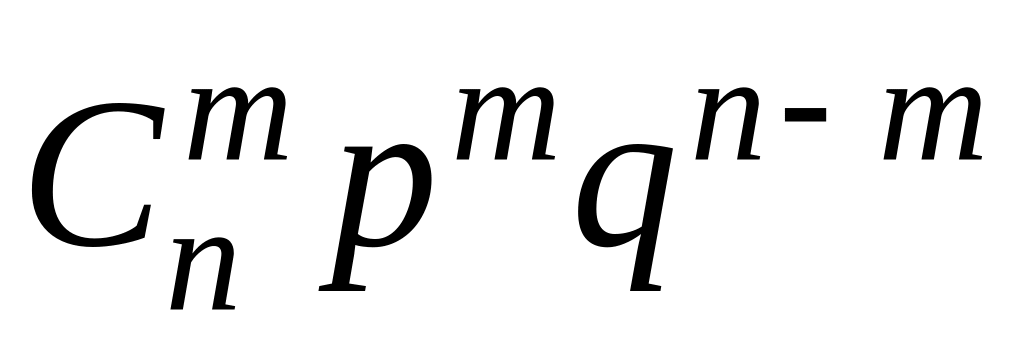1. Какова вероятность, что при 5 бросаниях игральной кости ровно 2 раза выпадет 6 очков?

Решение. В схеме Бернулли имеем параметры: п = 5; р = 1/6; q = 5/6. По формуле Бернулли получаем

Р₅(2) = = = = 0,16.

9. 1.8.2. Наиболее вероятное число успехов в схеме Бернулли m₀ удовлетворяет неравенству np – q  m₀  np + p.

Разность между границами этого неравенства равна 1, значит, в указанном промежутке обязательно есть целое число. Это число и есть искомое наиболее вероятное число успехов. При этом возможно, что целочисленными являются границы промежутка. В этом случае они являются двумя значениями наиболее вероятного числа успехов, соответствующие вероятности будут одинаковы.

2. Какое наиболее вероятное число выпадений 6 очков а) при 20; б) при 17 бросаниях игральной кости?

Решение. Воспользуемся теоремой 1.8.2:

а)  m₀  ;

 m₀  ;

m₂₀ = 3.

б)  m₀  ;

2  m₀  3;

m₀ = 2 или m₀ = 3.

При больших значениях п вычисления по формуле Бернулли становятся слишком громоздкими. В этом случае используются приближенные формулы.

10. 1.8.3 (локальная теорема Муавра – Лапласа). В схеме Бернулли при большом числе испытаний п имеет место приближенная формула

Р_n(m) = .

Эта формула дает хороший результат при п  30, при этом р должно быть не слишком близко к 0 или 1. Здесь функция (х) – это функция Гаусса, или плотность вероятностей. Она имеет вид (х) = . В практических вычислениях используется таблица значений этой функции, которая приводится практически во всех справочниках и учебниках по теории вероятностей. Эта функция четная, значит, при отрицательных значениях аргумента знак «–» отбрасывается. В таблицах для (х) обычно приводятся значения только для х  4, при x > 4 значение (х) можно считать равным 0.

3. Какова вероятность, что при 100 бросаниях игральной кости ровно 20 раз выпадет 6 очков?

Решение. В схеме Бернулли имеем параметры: п = 100; р = 1/6; q = 5/6. По локальной теореме Муавра – Лапласа вычисляем:

= 3,73;

Р₁₀₀(20) = = = = = 0,072.

Бывают ситуации, когда требуется вычислить вероятность того, что число успехов в схеме Бернулли принадлежит некоторому промежутку: a  µ_n  b. В этом случае можно отдельно посчитать и сложить вероятности для µ_n = a, a + 1, … , b. Но объем вычислений будет большой, и для таких случаев также используется приближенная формула.

11. 1.8.4 (интегральная теорема Муавра – Лапласа). В схеме Бернулли при большом числе испытаний п имеет место приближенная формула

Р_n(a  µ_n < b) = .

Область применения интегральной теоремы Муавра – Лапласа та же, что для локальной теоремы Муавра – Лапласа. Здесь используется функция

Ф(х) = ,

называемая интеграл вероятностей, ее таблица также приводится в книгах. Эта функция нечетная, то есть при наличии у аргумента знака «–» этот минус выносится за знак функции. Таблица значений этой функции обычно приводится только для х  4, при x > 4 значение Ф(х) можно считать равным 0,5. Следует иметь в виду, что в разных источниках функция Ф(х) определяется несколько по-разному, и это влияет на вид формулы в интегральной теореме Муавра – Лапласа. Таблица применима для приведенной выше формулы, если значения функции в конце таблицы приближаются к 0,5.

4. Какова вероятность, что при 100 бросаниях игральной кости 6 очков выпадет: а) от 15 до 20 раз; б) не менее 20 раз?

Решение. Воспользуемся решением примера 3: п = 100; р = 1/6; q = 5/6, = 3,73. По интегральной теореме Муавра – Лапласа получаем:

а) Р(15  µ_n  20) = Р(15  µ_n < 21) = = Ф(1,16) – Ф(–0,45) = 0,3370 + 0,1736 = 0,5106.

б) Р(µ_n  20) = Р(20  µ_n < 100) = =

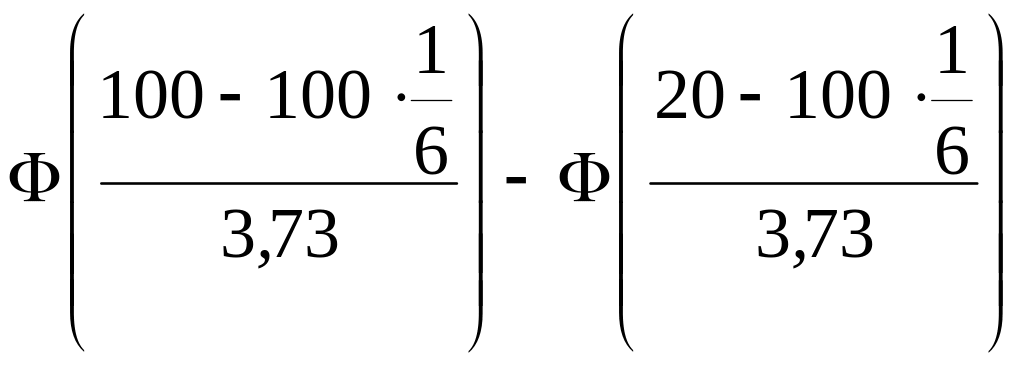= Ф(22,3) – Ф(0,89) = 0,5 – 0,3113 = 0,1887.