Упражнения

1. Проверить гипотезу о нормальном распределении для генеральной совокупности на уровне значимости α = 0,05 по следующему вариационному ряду.

   xi	20	23	26	29	32	35	38
   ni	5	4	10	19	18	15	1

2. Проверить гипотезу о нормальном распределении для экзаменационных оценок на уровне значимости α = 0,05 по данным экзаменационных оценок по какому-нибудь предмету среди студентов вашей группы.

2.5Корреляционная зависимость

В предыдущих главах часто встречались независимые случайные величины. Но на практике, конечно, встречаются разные степени зависимости. Крайний случай – функциональная зависимость, когда значения случайной величины Y однозначно определяются значениями случайной величины Х. Например, пусть в корзине лежат шарики разного размера, и случайным образом вытаскивается один шарик. Если Х – радиус шарика, а Y – его объем, то Y однозначно определяются через Х. Если же ввести третью случайную величину – массу шарика, то она может мало зависеть от Х, если шарики сделаны из разного материала.

Если рассмотреть связь между ростом и массой человека, то понятно, что в среднем с увеличением роста увеличивается масса. Но эта зависимость только средняя, для отдельных людей могут быть значительные отклонения в ту или другую сторону. Такая зависимость называется корреляционной.

В нашем примере эта зависимость проявляется следующим образом. Пусть Х – рост, Y – вес человека. Зададим произвольное значение х, например, х = 175 см, и определим средний вес людей с ростом 175 см. Это можно сделать для каждого значения х, получим соответствующие значения y. В результате возникает функция y = g(x), которая называется регрессией Y на Х. В нашем примере эта функция означает средний вес людей с ростом х.

Аналогично определяется функция x = f(y), задающая обратную зависимость – регрессия Х на Y. Графики этих функций называются линиями регрессии Y на Х и Х на Y соответственно.

Особенно важным является случай, когда линии регрессии являются прямыми линиями. Для независимых случайных величин значения g(x) и f(y) являются постоянными, линии регрессии параллельны координатным осям, значит, перпендикулярны друг другу. Чем теснее зависимость, тем меньше острый угол между этими линиями. Они пересекаются в точке с координатами (MX, MY). При функциональной зависимости линии регрессии совпадают.

Если случайные величины Х и Y независимы, то по свойствам математического ожидания M(XY) = MX ^. MY. Если же между Х и Y имеется зависимость, то это равенство нарушается, и за меру зависимости можно принять величину M(XY) – MX ^. MY. Но насколько велика степень зависимости можно понять, только если знать значения самих случайных величин Х и Y. Поэтому для характеристики степени зависимости принимают безразмерную величину, называемую коэффициентом корреляции:

r = .

Можно показать, что . При этом если r = 1, то между Х и Y имеет место функциональная линейная зависимость: прямая при r = 1, обратная при r = –1 (то есть при увеличении Х уменьшается Y). Если Х и Y независимы, то r = 0. Но обратное неверно. Между Х и Y может быть даже функциональная зависимость, но если она на одном участке прямая, а на другом обратная, то эти участки могут компенсировать друг друга и сделать коэффициент корреляции равным или близким к 0. Поэтому если r близок к 1, то мы делаем вывод, что зависимость тесная. Если же r близок к 0, то вывод о слабой зависимости еще требует своего подтверждения.

Характер зависимости можно проследить на графике. По результатам наблюдений получаем пары соответствующих значений Х и Y. Эти пары отмечаем точками на координатной плоскости. Если между Х и Y есть линейная корреляционная зависимость, то точки более или менее плотно заполняют наклонную полосу, и чем теснее зависимость, тем уже полоса. Линии регрессии проходят через эту полосу примерно посередине. Если же зависимость отсутствует, то точки будут образовывать более или менее широкое пятно, которое может быть вытянуто по горизонтали или вертикали. Линии регрессии будут пересекать его вертикально и горизонтально.

Для нахождения коэффициента корреляции и расчета уравнений прямых регрессии по данным выборки пользуются следующей таблицей.

i	xi	yi	xi –	yi –
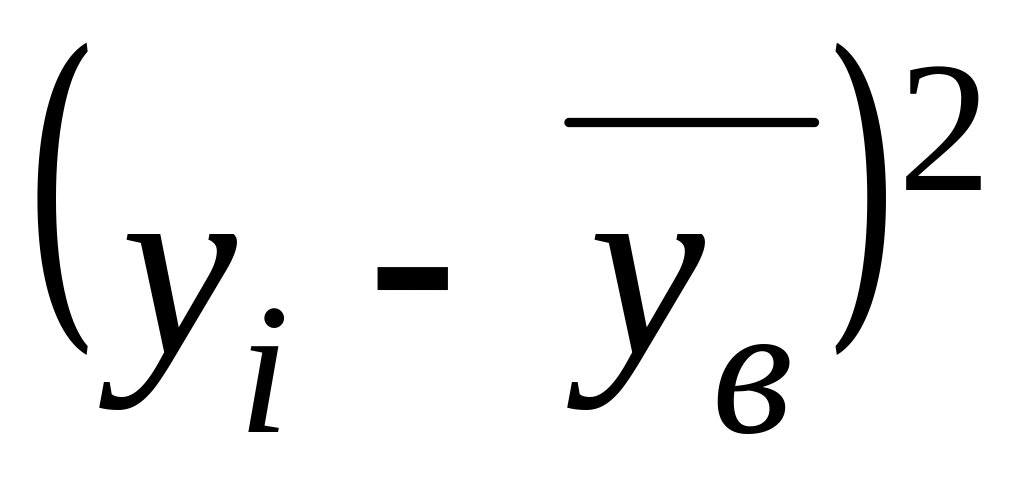
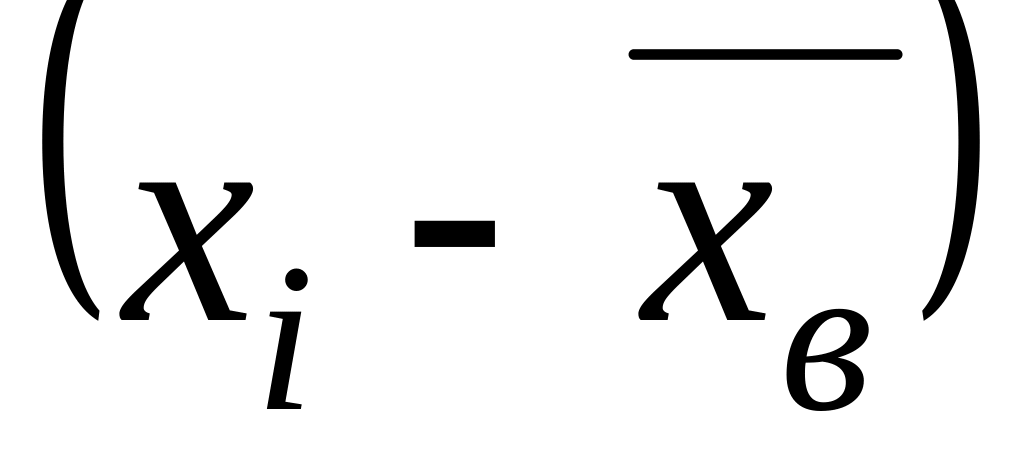
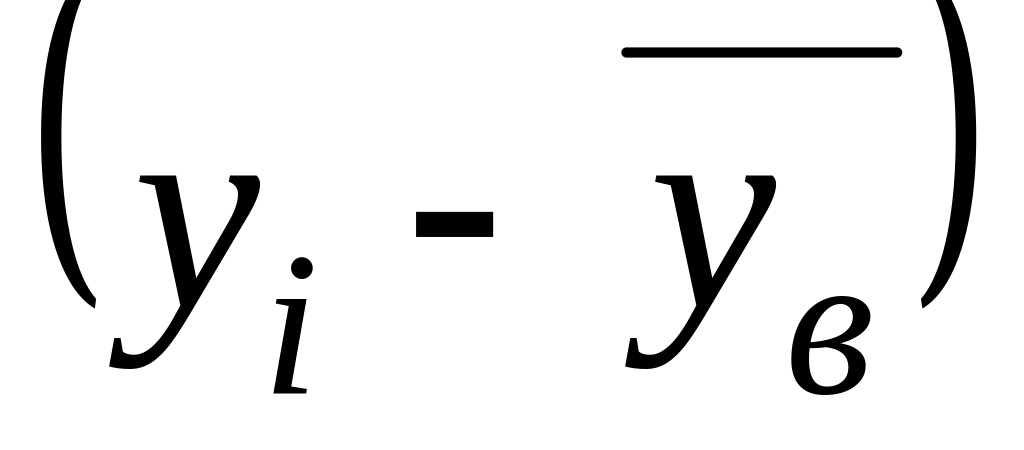
1 … n	x1 … xn	y1 … yn	 	 	 	 	 
Сумма	Σ1	Σ2			Σ3	Σ4	Σ5

Столбцы x_i и y_i – это исходные данные. Найдя их сумму, вычисляем

; .

При этом можно использовать ложный нуль, введя вспомогательные столбцы, как описано в разделе 2.2.

Заполняем, используя найденные значения, остальные столбцы. Далее вычисляем

; ; .

Найдя отсюда s_x и s_y, вычисляем коэффициент корреляции:

.

Выборочные уравнения прямых регрессии имеют вид

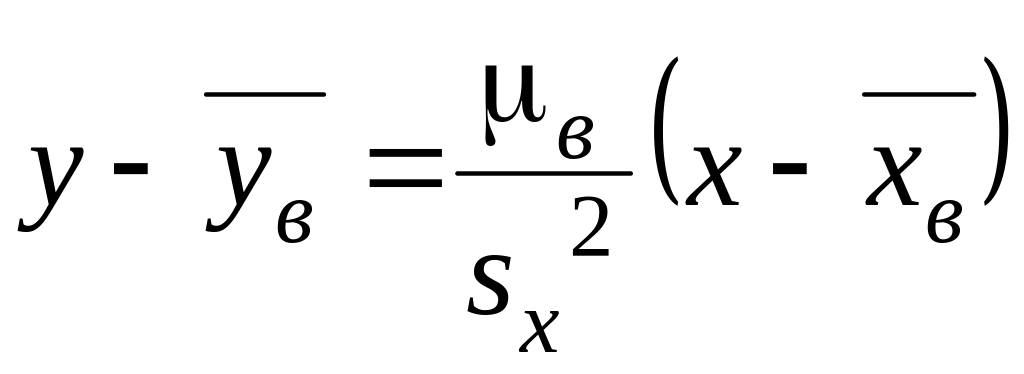– регрессия y на х;

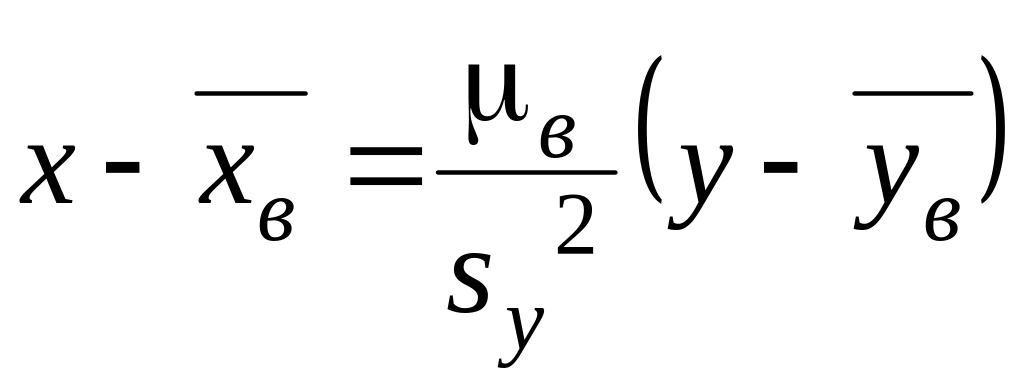– регрессия х на y.

1. Оценить степень и характер зависимости между случайными величинами Х и Y по данным выборки, приведенным в таблице. Получить уравнения прямых регрессии. Построить график.

xi	17	22	19	19	21	18	23	18	20	19
yi	48	65	45	53	59	51	64	59	60	60

Решение. Строим расчетную таблицу

i	xi	yi	xi –	yi –
1 2 3 4 5 6 7 8 9 10	17 22 19 19 21 18 23 18 20 19	48 65 45 53 59 51 64 59 60 60	–2,6 2,4 –0,6 –0,6 1,4 –1,6 3,4 –1,6 0,4 –0,6	–8,4 8,6 –11,4 –3,4 2,6 –5,4 7,6 2,6 3,6 3,6	6,76 5,76 0,36 0,36 1,96 2,56 11,56 2,56 0,02 0,36	70,56 73.96 129,96 11,56 6,76 29,16 57,76 6,76 12,96 12,96	21,84 20,64 6,84 2,04 3,64 8,64 25,84 -4,16 1,44 -2,16
	196	564			32,26	412,4	84,6

= 19,6;

= 56,4;

= 3,58; = 1,89;

= 45,8; = 6,77;

=9,4;

= 0,73.

Так как r близок к 1, то связь между Х и Y достаточно тесная и прямая.

Найдем уравнения прямых регрессии

;

y – 56,4 = 2,6x – 51,4;

y = 2,6x + 5 – уравнение прямой регрессии Y на X;

;

x – 19,6 = 0,21y – 11,6;

0,21y = x – 8;

y = 4,8x – 38,1 – уравнение прямой регрессии X на Y.

Строим график. Для проведения прямых регрессии найдем на них по две точки. Для этого зададим значения х и определяем соответствующие значения у по найденным формулам.

Прямая регрессии Y на X:

x = 17  y = 2,6 ^. 17 + 5 = 49,2;

x = 23  y = 2,6 ^. 23 + 5 = 64,8.

Прямая регрессии X на Y:

x = 17  y = 4,8 ^. 17 – 38,1 = 43,5;

x = 22  y = 4,8 ^. 22 – 38,1 = 67,5.

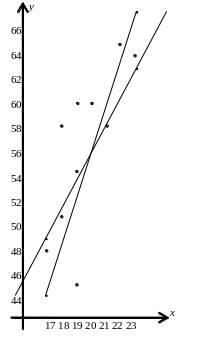
Прямая регрессии Y на X на графике менее крутая, чем прямая регрессии X на Y; это является общим правилом.