Задания для контрольной работы

Каждый студент подставляет в задания свои значения параметров а и b.

1. Сколькими способами из группы в (10+a+b) человек можно выбрать двоих делегатов на конференцию?

2. Сколькими способами из группы в (15+a+b) человек можно выбрать старосту и его заместителя?

3. По мишени производятся три выстрела. Выразить через события А_k – «попадание при k-ом выстреле», (k = 1, 2, 3), следующие события:

   Значение b	Событие
   1; 5	Хотя бы одно попадание
   2; 6	Три попадания
   3; 7	Три промаха
   4; 8	Хотя бы один промах

4. В урне 5 черных, а красных и b белых шара. Наудачу вынимаются 3 шара. Какова вероятность, что все они разного цвета?

5. Какова вероятность, что при бросании двух игральных кубиков в сумме выпадет a+b очков?

6. Два стрелка одновременно стреляют по мишени. Вероятности попадания для них равны соответственно 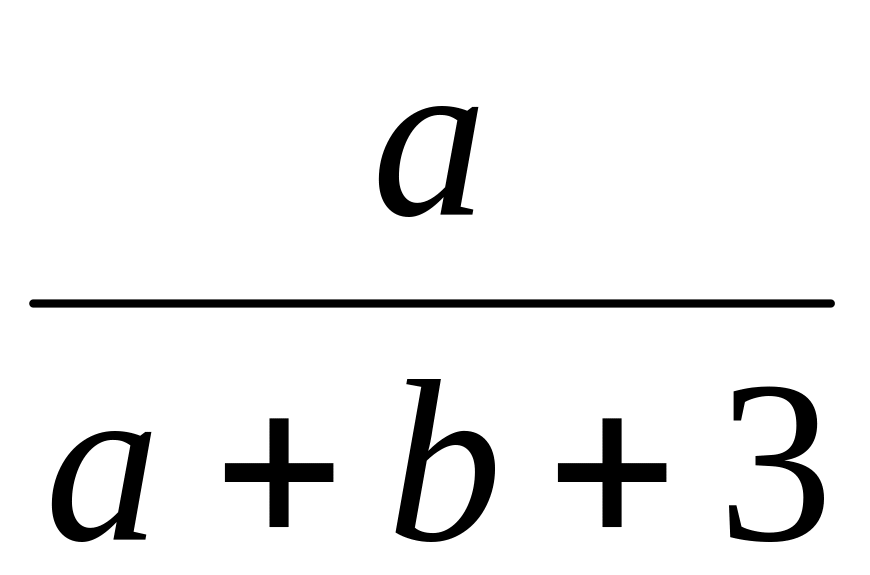и . Какова вероятность: а) хотя бы одного попадания; б) двух попаданий?

7. Из карточек с буквами составлена Ваша фамилия. Составьте из этих карточек (не обязательно всех) какое-нибудь слово. Какова вероятность, что при случайном извлечении нужного числа карточек и выкладывании их в ряд получится это слово?

8. На сборку поступают детали из двух цехов: 40% из первого и 60% из второго. В продукции первого цеха а% брака, второго – (a+b)%. Какова вероятность, что наудачу взятая деталь окажется бракованной?

9. Производятся 7 выстрелов по мишени с вероятностью попадания при одном выстреле а/10. Какова вероятность, что будет ровно b попаданий? Какое наиболее вероятное количество попаданий?

10. Производится 100 испытаний с вероятностью успеха в одном испытании . Найдите вероятность того, что число успехов: а) равно a+10b+20; б) заключено в пределах от a +10b+10 до 10b+25; в) не меньше a +10b+15.

11. Случайная величина Х задана таблицей:

Х	0	a	a+b	a+b+1
р	0,1	0,4	0,3	0,2

Найдите функцию распределения F(x) и постройте ее график. Найдите математическое ожидание, дисперсию и среднее квадратичное отклонение.

12. Непрерывная случайная величина задана Х функцией распределения:

Найдите плотность вероятности f(x). Найдите вероятность того, что Х примет значение из интервала .

2.Математическая статистика.

2.1Выборочный метод

Для того, чтобы принимать правильные решения в экономике, политике, коммерции и других областях деятельности, необходимо владеть информацией. Информацию получают как в процессе обычной работы из отчетов подразделений и других документов, так и в ходе специальных исследований, которые проводят статистические службы. Полученную информацию надо уметь обработать, чтобы на ее основе составлять прогнозы и планы.

Прогнозы в экономике в условиях конкуренции должны быть очень точными. Если спрос на производимый товар окажется меньше ожидаемого, то это приведет к потерям на производство ненужного товара. Если же спрос окажется выше, то это будет означать недополученную прибыль. Совершенно точно спрогнозировать спрос, конечно невозможно, и надо уметь определять его границы и вероятность отклонения от этих границ. Принятое решение должно обеспечить максимальную прибыль.

Объекты статистического изучения могут быть самые разные. Это может быть и распределение размеров одежды у потенциальных покупателей, и технические параметры произведенной промышленной продукции, и содержание полезных веществ в выращенной сельскохозяйственной продукции, и оценки учеников на экзаменах, и многое другое. Изучаемая в данном статистическом исследовании совокупность объектов называется генеральной совокупностью; количество этих объектов – объем генеральной совокупности. Выделяется один или несколько параметров, которые необходимо изучить. Значение параметра является случайной величиной, у каждого объекта генеральной совокупности оно свое. Задача статистики – определить закон распределения этой случайной величины. Если у каждого объекта генеральной совокупности можно измерить значение параметра, то мы получим полную и точную информацию о законе распределения. Но обычно это невозможно. Объем генеральной совокупности может быть очень большой. Изучение параметров продукции может сопровождаться ее уничтожением, например, при определении боевых характеристик произведенной партии снарядов. Поэтому для изучения генеральной совокупности из нее производят выборку, то есть отбирают некоторое количество объектов для непосредственного изучения.

Обязательное условие для выборки – ее репрезентативность. Оно означает, что выборка должна равномерно представлять всю генеральную совокупность. Не является репрезентативной, например, выборка для изучения характеристик урожая яблок из сада, если в выборку попадают плоды с одного дерева. Не является репрезентативным и результат социологического опроса, производимого по телефону в рабочее время: участвовать в опросе будут в основном пенсионеры и домохозяйки.

Выборка может быть повторной или бесповторной. При повторной выборке ее объекты отбираются по одному и после изучения возвращаются в генеральную совокупность. Каждый объект может попасть в выборку любое число раз. При бесповторной выборке все ее объекты различные. Оказывается, повторная выборка более правильно отражает распределение изучаемого признака в генеральной совокупности. Но если объем выборки мал по сравнению с объемом генеральной совокупности, то принципиальной разницы между повторной и бесповторной выборкой нет.

Пусть изучается распределение значений признака Х (являющегося случайной величиной). В результате измерения получаем набор его значений для объектов выборки. Каждое его значение называется вариантой, а весь набор значений – вариационным рядом.

Каждая варианта может встречаться один или несколько раз. Количество ее появлений n_i в выборке называется ее частотой, а отношение n_i/n частоты к общему объему выборки называется относительной частотой. Диаграмма, на которой показаны значения частот или относительных частот для вариант выборки, называется полигон частот. На этой диаграмме значения частот для каждой варианты отмечаются точками, и эти точки последовательно соединяются отрезками.

Если значений вариант очень много, то их следует сгруппировать в интервалы, обычно одинаковой ширины. Количество и ширина интервалов определяются объемом выборки и задачами исследования. Например, при производстве одежды один из параметров – рост человека, для него приняты интервалы шириной 6 см. Частотой для каждого интервала будет количество значений изучаемого признака, попавших в этот интервал. Диаграмма, изображающая распределение частот для интервального распределения, называется гистограммой, она имеет столбчатую форму.

Выделяются несколько числовых характеристик, описывающих вариационный ряд и позволяющих сравнивать вариационные ряды между собой.

Выборочное среднее – это среднее арифметическое всех выборочных значений. Для вариационного ряда x₁, … , x_n оно вычисляется по формуле

.

Если для выборки объема п указаны выборочные значения x₁, … , x_m и соответствующие частоты n₁, … , n_m, то пользуемся формулой

.

Этой же формулой пользуемся, если вариационный ряд имеет интервальный вид. В качестве значений x_i в этом случае берем середины соответствующих интервалов.

Мода вариационного ряда – это варианта, встречающаяся чаще всех других. Если таких вариант несколько, то мода имеет несколько значений. Если все варианты встречаются одинаково часто (в частности, по одному разу), то моды нет. Смысл этого термина близок к смыслу обычного термина «мода»: это самое «модное» значение.

Среди значений вариант может встретиться значение, сильно отличающееся от основной массы значений. Оно является случайным, не характерным для всей генеральной совокупности, но может существенно повлиять на значение выборочного среднего. Поэтому в дополнение к выборочному среднему находят медиану вариационного ряда. Для этого все варианты выписывают в порядке возрастания, повторяя их столько раз, какова их частота. Медиана – это значение варианты, оказавшейся в центре получившейся последовательности. Если ее длина четная, то в центре окажутся два числа, и медиана – это их среднее арифметическое. Если вариационный ряд задан таблицей с частотами для вариант, то центральные числа находятся по их номерам, без выписывания всего ряда в строку.

Размах вариационного ряда – это разность между максимальным и минимальным значениями вариант.

1. Дан вариационный ряд 5, 1, 3, 4, 2, 2, 4, 1, 2, 5. Найти его выборочное среднее, моду, медиану, размах. Построить полигон частот.

Решение. Объем выборки п = 10. Выборочное среднее

= 2,9.

Выпишем значения вариационного ряда в порядке возрастания:

1, 1, 2, 2, 2, 3, 4, 4, 5, 5.

Мода равна 2, так как это значение имеет наибольшую частоту, равную 3. Медиана равна = 2,5, это среднее арифметическое двух центральных значений. Размах равен 5 – 1 = 4. Полигон частот имеет вид