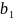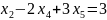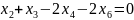Раздел 1.

Линейное программирование.

Глава 1. Метод линейного программирования

Сведение общей задачи ЛП к равносильной ей основной задаче путём введения добавочных неизвестных.

Общей задачей ЛП является отыскание наибольшего или наименьшего значения линейной функции на множестве неотрицательных решений линейной системы неравенств или системы: неравенства + уравнения.

В основной задаче ЛП линейная система содержит только уравнения:

Минимизировать (максимизировать):

при условиях

Общая задача ЛП может быть сведена к равносильной ей основной задаче путём введения добавочных неизвестных. Например, дана общая задача

при условиях

.

Здесь показатель качества и ограничения линейны относительно неизвестных. Сведем общую задачу ЛП к равносильной ей основной задаче:

при условиях

;

.

Между общей задачей ЛП и соответствующей ей основной существует связь. Если оптимальное решение (оптимальный план) основной задачи, то – оптимальное решение общей задачи и наоборот. Причем оптимальные значения целевых функций совпадают:

Таким образом, удалив из оптимального решений основной задачи значения добавочных неизвестных, получим оптимальное решение общей задачи. Если основная задача не имеет решения, то и общая задача также не имеет решения.

Задача ЛП является задачей максимизации, если находят и минимизации, если находят .

В литературе могут также встретиться и другие формы записи общей и основной задач ЛП [1-4]:

1. Максимизировать (минимизировать) функцию цели

переменные которой подчинены следующим условиям:

.

2. Минимизировать

3. Минимизировать при условиях , где

– вектор-строка; - вектор-столбец; – матрица коэффициентов системы ограничений;

– вектор-столбец.

§1. Примеры составления задач лп

Формулировка задачи о рациональном питании [2].

Для сохранения здоровья и работоспособности человек должен потреблять в сутки определенное количество питательных веществ (белков, жиров, углеводов, воды, витаминов), запасы которых в различных видах пищи ( ) различны. Ограничимся, например, двумя видами пищи .

Питательные вещества	Норма суточная		Виды пищи
Жиры
Белки
Углеводы
Вода
Витамины

Здесь – запас жиров в единице (например, в 1 кг) пищи вида и т.д. и – стоимость единицы (1 кг) пищи вида и . Требуется так организовать питание, чтобы стоимость его была наименьшей, а организм получил бы не менее минимальной суточной нормы питательных веществ всех видов пищи.

Пусть – количество (например, в кг) пищи видов и , потребляемых человеком в сутки. Тогда общие запасы жиров в двух видах пищи не должны быть меньше минимальной нормы , т.е. и т.д., всего 5 неравенств (обратить внимание на знак ). Общая стоимость питания , т.е. имеем следующую задачу ЛП:

при условиях:

;

;

;

;

;

Формулировка транспортной задачи

Необходимо перевезти некоторое количество единиц однородного товара из двух складов в три магазина (обратные перевозки исключаются). Склады могут выделить

единиц товара, а магазинам требуется единиц товара.

Предполагается, что , т.е. существует между складами и

магазинами баланс. Необходимо определить, сколько единиц товара

( ) надо отправить с каждого склада в каждый магазин, что

общая стоимость перевозки была минимальна, если –

стоимость перевозки товара от складов к магазинам. Зависимость стоимости

перевозки от количества перевозимого товара предполагается линейной.

Задача ЛП записывается следующим образом:

при условиях:

Решением задачи является . При этом минимальна.

Аналитическая идея симплексного метода

Линейная система уравнений называется системой с базисом, если в каждом уравнении содержится неизвестное с коэффициентом +1, отсутствующее в остальных уравнениях. Эти неизвестные называются базисными, оставшиеся – свободными. Число базисных неизвестных равно числу уравнений.

Линейная система уравнений называется канонической, если она является системой с базисом, а все В данном выше числовом примере система уравнений является канонической.

Примеры канонических систем:

1. 

2. 

Примеры неканонических систем:

1. 

Система неканоническая, так как один из свободных членов отрицателен.

2. 

Система неканоническая, так как в системе отсутствует базис.

3. Система неканоническая, так как в системе отсутствует базис.

Чтобы перейти к каноническому виду, необходимо в первом случае 2-е уравнение умножить на (-1), а затем во всех трех случаях ввести базис (полностью или частично).

При больших значениях m и n трудно найти оптимальное решение путем перебора всех его допустимых решений. Поэтому существует упорядоченная схема перебора, получившая название симплексного метода [1-4]. Поясним аналитически идею симплексного метода на следующем примере:

при условиях

По теореме Кронекера-Капелли [2] для совместности линейной системы необходимо и достаточно, чтобы ранг матрицы A r(A) был равен рангу расширенной матрицы R r(R). r(A) есть наибольший из порядков миноров, отличных от нуля (т.е. r(A) – целое число). Известно, что r(A) не меняется, если к какому-либо столбцу (строке) прибавить произвольную линейную комбинацию других столбцов (строк) этой матрицы. Кроме того, r(A) не изменится, если какой-либо столбец, состоящий из нулей, удалить. Итак

= ?

Прибавив первый столбец, умноженный на (-1), к пятому, а затем и к четвертому, получим

Выполняем аналогичные преобразования и, в итоге, получим

Соответственно, ранг расширенной матрицы будет равен также

= 3.

Следовательно, наша система совместна.

При формулировке задач ЛП могут быть два случая:

1. ( – количество неизвестных в системе).

Решение системы единственное. Задача ЛП не имеет смысла.

2. . Этот случай представляет для нас интерес. Неизвестных больше, чем уравнений в системе. Задаваясь каждый раз свободными неизвестными, получим в итоге множество решений системы, из которых в соответствии с функцией цели выбирается то решение, которое дает оптимальный результат. В нашем примере

Как было показано выше, в исходном числовом примере система уравнений каноническая.

Итак,

(1)

при условиях

В системе базисных переменных три , а свободных два . Выразим целевую функцию и базисные переменные через свободные переменные .

Но F уже выражена, а базисные переменные примут следующий вид:

( 2 )

( 3 )

Все должны быть неотрицательны, т.е. .

Зададим наименьшие возможные значения , при этом получим . Это решение, удовлетворяющее ограничениям, т.е. допустимое. Проанализируем, нельзя ли увеличением значений уменьшить ? Из выражения

следует, что при увеличении возрастает. При будет отрицательным самый ненадёжный из , Значит, следует принять . Тогда получим новый допустимый план: При этом Переменное выведено из базиса, вместо него в базис включен а стали свободными переменными. Выразим новые базисные переменные и функцию F через . найдём . Подставим в выражения

(1), (2), (3). Получим:

Из выражения следует, что должны быть равны нулю, так как в противном случае F будет расти.

Достигнуто оптимальное решение:

Полученное решение называется базисным, так как свободные переменные равны нулю. Следует отметить, что оптимальное решение получено, когда в выражении для F полученные значения коэффициентов при неизвестных положительны, а в процессе решения значение F только понижалось от 3 до 1, т.е. перебор был организованным.

Пример. Найти минимальное значение целевой функции

на множестве решений системы

Решение. Здесь - свободные переменные. Перепишем систему ограничений (1) в виде

Исходным базисным решением является решение (7; 0; 0; 12; 0; 10), при котором значение функции равно нулю. Целевая функция уже выражена через небазисные переменные. Значение целевой функции может быть уменьшено за счет увеличения . Среди коэффициентов при в системе (2) имеются отрицательные: и . Находим отношения (из второго уравнения системы (2)): . Элемент – разрешающий. Из старого базиса исключим и введем в него из небазисных переменных . Для этого выразим через и из второго уравнения и найденное выражение подставим вместо в первое и третье уравнения системы (2), а также в выражение F.

Получим систему (3), где - свободные переменные.

Новое базисное решение имеет вид: (10; 0; 3; 0; 0; 1). . Значение F можно уменьшить за счет увеличения . Среди коэффициентов при в системе (3) только один отрицательный: Элемент разрещающий. Перейдем к новому базису:

Новое базисное решение имеет вид: , Дальнейшее уменьшение значения целевой функции невозможно.

Практическое решение задач линейного программирования, как правило, обычно проводится так: коэффициенты при переменных переписываются в специальные таблицы – симплексные таблицы (собственно мы это уже сделали при нахождении базисных решений системы линейных уравнений).