§6. Параметрическое программирование.

(6.1)

Для всех значений параметра где – произвольные действительные числа, найти такие значения , которые обращают в минимум линейную формулу

при условиях:

или краткой форме:

,

заданные постоянные.

Задачу решают в следующем порядке.

1. Пользуясь симплекс-методом, решаем задачу (6.1) – (6.3) при до получения оптимального плана.

Коэффициенты линейной формы равны:

(6.4)

Следовательно, для любого базиса разности могут быть представлены в виде линейной функции от , то есть

(6.5)

Тогда

(6.6)

что означает совместность всей системы неравенств

(6.7)

Решение задачи (6.1) – (6.3) , полученное при , является оптимальным для всех значений параметра , удовлетворяющих условию

г

(6.8)

де

( 6.9)

Здесь возможны следующие случаи:

а) , процесс решения закончен. Полученный план при остается оптимальным для всех значений параметра

б) , при . Если все , то линейная форма (6.1) при не ограничена снизу. Полученный план при остается оптимальным для всех значений параметра ;

в) и существует по крайней мере одна . В этом случае в базис вводится вектор и исключается вектор . Новый базис соответствует оптимальному плану хотя бы для одного значения параметра .

Если интервал является полной совокупностью значений , для которых новый базис соответствует оптимальному плану, то . Полученный оптимальный план при остается оптимальным для всех значений параметра . Полагая далее , продолжают процесс решения задачи. Аналогичным образом переходят от одного интервала изменения к другому, пока один из интервалов не включит .

Величины называют критическими значениями параметра , а оптимальные планы, соответствующие различным значениям – критическими решениями.

2. Пользуясь симплекс-методом, можно убедиться, что при линейная форма не ограничена снизу на выпуклом множестве, определяемом условиями (6.2).

Здесь возможны следующие случаи:

а) – вектор, подлежащий вводу в базис, , все Если , то линейная форма задачи не ограничена снизу для любого

б) если , неравенство 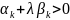будет иметь место для всех , то есть для любого задача не имеет оптимального плана. Если все , то оптимальный план задачи получен.

Пусть , тогда этот план является решением задачи при , а далее решение продолжается так же, как в случае (а).

Если не все , в базис вводится любой вектор, для которого . Процесс продолжается до тех пор, пока не окажется, что , или пока не будет обнаружен вектор c , все коэффициенты разложения которого по базису неположительны.

Если для всех j, встречаем случай (а).

Если , линейная форма задачи не ограничена снизу при всех .

Если , то линейная форма при , где ’ > , не ограничена снизу.