Раздел 2. Нелинейное программирование

Глава 1.

§ 1. Задачи нелинейного программирования с линейной целевой функцией и нелинейной системой ограничений.

Чтобы проиллюстрировать более наглядно различие между линейными и нелинейными задачами, ограничимся решением задачи с двумя переменными, так как решение таких задач может быть представлено графически.

Задача.

На множест­ве решений системы неравенств

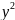+ ≤ 36;

найти глобальные экстремумы функции .

Решение. На рис. 1 множество допустимых реше­ний заштриховано. Это мно­жество выпукло. Линиями уров­ня функции z = 2х + у являют­ся параллельные прямые с уг­ловым коэффициентом К = - 2. Очевидно, что глобальный ми­нимум достигается в точке О(0; 0), а глобальный макси­мум— в точке А касания пря­мой уровня и окружности х² ± y² = 36. Найдем координа­ты точки А. Для этого доста­точно составить уравнение пря­мой l и решить систему, со­стоящую из уравнения прямой и уравнения окружности. За­метим, что прямая l перпенди­кулярна линии уровня, а, следо­вательно, ее угловой коэффици­ент К₁ равен (К₁К = — 1). Прямая l проходит через точку О и имеет угловой коэффициент

К ₁ = .

Рис. 1

Поэтому ее уравнение таково: у = .

Решая систему

+ = 36;

у = ,

получаем

Итак, глобальный минимум, равный 0, достигается в точке О (0;0), а глобальный максимум, равный 6 , — в точке А (2,4- ; 1,2* ). Локальных экстремумов, отличных от глобальных, функция не достигает.

§ 2. Задачи нелинейного программирования с линейной системой ограничений, но нелинейной целевой функцией.

Множество допустимых решений таких задач всегда выпукло, так как линейные ограничения образуют выпуклый многогранник в n-мерном пространстве. Однако в отличие от линейного программирования при нелинейной целевой функции оптимальное решение не обязательно нахо­дится в вершине этого много­гранника.

Задача.

Определить наибольшее значение функции z = при условии

Решение. Множество до­пустимых решений заштрихова­но на рис. 2. Если целе­вой функции придавать фикси­рованные значения с, то будем получать окружности с центром в начале координат и радиусом с². Пусть с = 1, 2, ... Начертим ряд окружностей (линии уров­ня целевой функции). Из рисунка 2 видно, что функция z = достигает наиболь­шего значения, равного 8, в точ­ке A (8;0): z = 8.

Рис.2

К рассматриваемому типу нелинейных задач относятся и за­дачи с дробно-линейной целевой функцией.

Решение задач дробно-линейного программирования

симплексным методом

Дробно-линейной функцией называется функция вида

Задача. Найти максимальное значение функции

на множестве решений системы ограничений

Решение. Введем обозначение:

Тогда

Обозначим Целевая функция запишется тогда так:

Преобразуем систему ограничений, умножив обе части всех ограничений на :

Включим в систему ограничений (2) ограничение (1) и перейдем к переменным

Нетрудно убедиться в том, что мы получили задачу линейного программирования:

найти максимальное значение на множестве решений системы (3). Эту задачу линейного программирования решаем симплексным методом, обозначив и учитывая, что