Лабораторная работа № 4

Тема: Матричные операции в Excel. Работа с матричными объектами: векторы, матрицы, массивы. Основные операции с матрицами. Транспонирование, обращение матриц. Вычисление детерминанта матриц. Решение систем линейных уравнений.

Цель работы. Получить практические навыки по работе с матричными функциями в Excel, научиться вычислять корни системы линейных уравнений посредством Excel.

Ход работы

М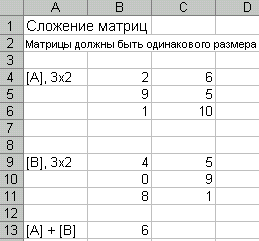 атрицей называется набор значений, упорядоченный в виде столбцов и строк.

Матрица, состоящая из одной строки или одного столбца наз. вектором.

Сложение матриц. Складывать матрицы можно только при условии их одинакового размера.

Формула для ячейки В13 будет выглядеть так: =В4+В9. Если теперь попеременно скопировать содержимое ячейки В12 в диапазон ячеек В13:С15, Excel попеременно сложит матрицы [А] и [В].

Откройте приложение Microsoft Excel. Созданный документ должен быть сохранен в папке, созданной по типу: D:\PF\28\Фамилия, под названием лр№4. Создайте таблицу, изображенную на рис. Выполните сложение матриц.

Н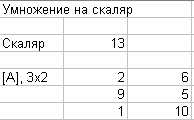 азовите лист сложение матриц, и перейдите на следующий.

У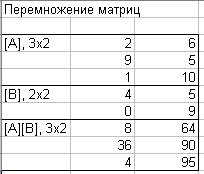 множение матрицы на скаляр. Чтобы умножить матрицу на скаляр, необходимо умножить на скаляр каждый элемент матрицы. Выполните умножение. Назовите лист умножение на скаляр, и перейдите на следующий.

Перемножение двух матриц. Две матрицы можно перемножить, если количество столбцов первой матрицы равно количеству строк второй матрицы. В начале процесса следует указать, где будет находиться матрица. (Примечание: следует указывать реальный размер, состоящий из «внешних» размеров перемножаемых матриц, с правильным количеством ячеек; однако если нужные размеры заранее неизвестны, лучше выбрать слишком большой диапазон ячеек, чем слишком маленький.) Указав местоположение новой матрицы, следует воспользоваться функцией МУМНОЖ(массив1;массив2) где Массив1, массив2 — перемножаемые массивы. Для того, чтобы закончить функцию перемножения матриц, необходимо нажать комбинацию клавиш <Ctrl+Shift+Enter>. Назовите лист умножение матриц, и перейдите на следующий.

Транспонирование матриц. Чтобы транспонировать матрицу достаточно просто поменять местами ее строки и столбцы.

Назовите лист транспонирование, и перейдите на следующий.

Обращение матриц. Используя функцію МОБР(матрица) самостоятельно вычислить обратную матрицу.

Назовите лист обращение, и перейдите на следующий.

Вычисление детерминанта (определителя). Для вычисление детерминанта используется функция МОПРЕД(матрица).

Примечание: при вычислении детерминантов больших матриц выполняется масса операций, что может привести к значительной ошибке округления. Ненулевой, но очень маленький детерминант (порядка 10^-14), вероятно является ошибкой округления, и скорее всего, в данном случае детерминант не существует.

Используя функцію МОПРЕД(матрица) самостоятельно вычислить определитель матрицы.

Назовите лист определитель, и перейдите на следующий.

Решение систем линейных уравнений.

Выполните процесс решения системы линейных уравнений, изображенный на рисунке.

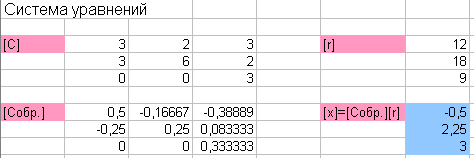
Назовите лист система уравнений.

Произведите вычисления на новом листе с произвольными данными.

Проанализируйте значения детерминанта.

Продемонстрируйте результаты работы преподавателю.