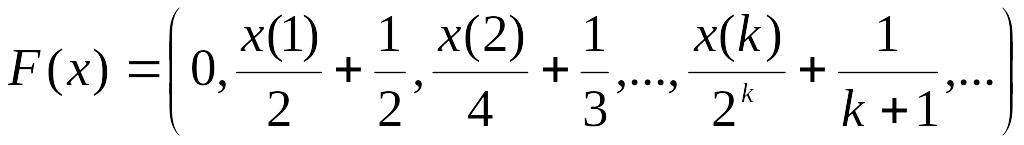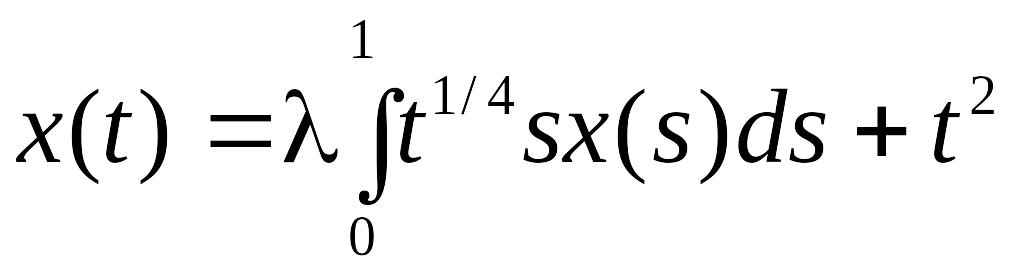Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Гомельский государственный университет им. Франциска Скорины

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

макет ФАН ч 2_1.doc

Скачиваний:

Добавлен:

01.05.2025

Размер:

3.31 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 77

Тема 2.6

Сжимающие отображения

Всюду ниже - метрическое пространство.

Определение. Отображение называется сжимающим, если оно удовлетворяет условию Липшица с константой Липшица . Другими словами, существует такое , что при всех выполняется неравенство

Определение. Точка из Х называется неподвижной для отображения , если .

Теорема (принцип сжимающих отображений). Сжимающее отображение А полного метрического пространства в себя имеет неподвижную точку, причем ровно одну.

При этом неподвижная точка может быть найдена методом последовательных приближений (итераций), т.е. как предел последовательности, заданной рекуррентным соотношением , где выбирается произвольно.

Оценка абсолютной погрешности приближенного равенства дается формулой

Теорема. Пусть k(t,s) и g(t) - непрерывные функции ( ). Отображение

в пространстве является сжимающим, если и только если , где . При этом .

2.6.1. Является ли отображение F метрического пространства X в себя сжимающим? Найти , где . Оценить расстояние от до неподвижной точки в случае, если F является сжимающим (таблица 2.6.1).

Таблица 2.6.1

Вариант	X	F
1
2
3
4
5
6
7
8
9
10

2.6.2. Применим ли принцип сжимающих отображений к заданному интегральному уравнению в пространстве Х при ? При найти приближенное решение с точностью до 0,01 и сравнить его с точным решением (таблица 2.6.2).

Таблица 2.6.2

Вариант	Х		Уравнение
1
2
3
4		1
5
6
7
8
9
10

Примеры решения типовых задач

1. Является ли отображение F метрического пространства X в себя сжимающим? Найти , где . Оценить расстояние от до неподвижной точки, если F является сжимающим.

Пример 1. .

Решение. Оценим расстояние в :

(мы воспользовались неравенством ). Значит, F является сжимающим отображением с константой Липшица .

Построим последовательность . По условию, . Поэтому , ,

А так как , где – неподвижная точка, то

Пример 2. , .

Решение. Оценим расстояние в :.

Значит, – сжимающее отображение с константой Липшица . По условию, . Тогда а потому

Пример 3. .

Решение. Допустим, что отображение F является сжимающим, то есть . При из последнего неравенства следует, что

. (1)

Подставив в левую часть неравенства (1), получим

при

(мы воспользовались соотношением при ). Правая же часть неравенства (1), как легко проверить, при этом значении х равна . Следовательно, неравенство (1) при указанных x, y и примет вид - противоречие. Значит, F не является сжимающим. (Аналогичное решение получается и при ).

2. Применим ли принцип сжимающих отображений к заданному интегральному уравнению в пространстве Х при ? При найти приближенное решение с точностью до 0,01 и сравнить его с точным решением.

Пример 1. . (2)

Решение. Определим отображение формулой

Тогда исходное уравнение запишется в виде , и искомое решение есть неподвижная точка отображения f. Метрическое пространство является полным, поэтому, если мы покажем, что f – сжимающее отображение в себя, то можно будет применить принцип сжимающих отображений.

То, что отображение f непрерывную на функцию переводит в непрерывную, в данном случае очевидно (а в общем следует из свойств интеграла, зависящего от параметра). В силу соответствующей теоремы отображение f является сжимающим, если и только если , где . При этом константа Липшица . В нашем случае , . Следовательно, является сжимающим, если и только если , т.е. при и , и не является сжимающим при .

Решим уравнение (2) приближенно при . При этом отображение является сжимающим, а значит для нахождения приближенного решения можно воспользоваться методом итераций. Поскольку выбирается произвольно, возьмём . Дальнейшие приближения находятся по формулам , .

Установим номер k, при котором элемент будет давать точность приближения 0,01. Используя оценку абсолютной погрешности (х − точное решение), находим n из неравенства