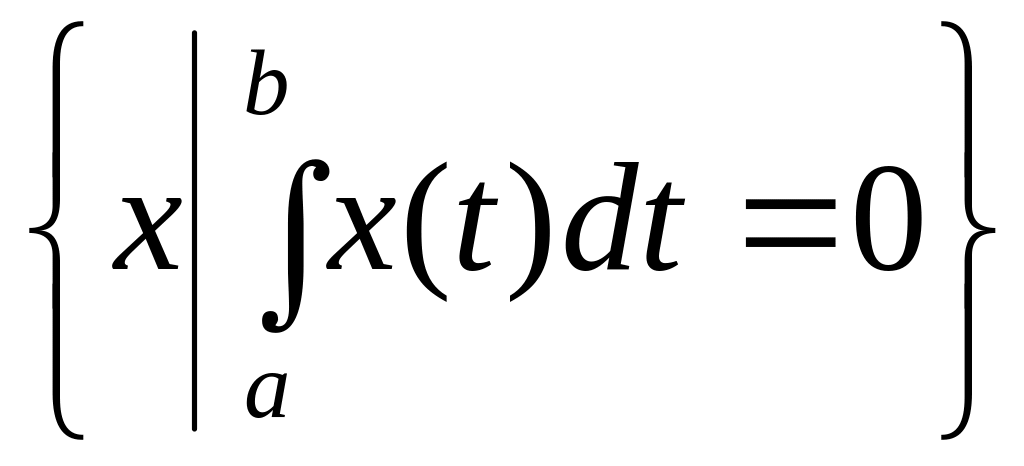Тема 2.2

Топология метрических пространств

Всюду ниже - метрическое пространство.

Определение. Пусть . -окрестностью точки а называется открытый шар с центором в точке а радиуса , т. е. множество

Определение. Пусть . Точка а называется внутренней точкой множества А, если она принадлежит А вместе с некоторой своей -окрестностью.

Определение. Множество всех внутренних точек множества А обозначается и называется внутренностью множества А.

Определение. Множество называется открытым, если каждая его точка внутренняя.

Определение. Множество называется замкнутым, если его дополнение открыто.

Определение. Пусть . Наименьшее замкнутое множество, содержащее А, называется замыканием множества А и обозначается (или ).

Теорема (о принадлежности замыканию). Пусть . Следующие утверждения равносильны:

1) ;

2) для любого ;

3) для некоторой последовательности точек множества А.

Определение. Если точка удовлетворяет условию 2) (или, что равносильно, 3)) предыдущей теоремы, то она называется точкой прикосновения множества А.

Следствие. Замыкание множества А равняется объединению множества А и множества его точек прикосновения.

Определение. Границей множества А называется множество

.

Точки границы называются граничными точками множества А.

Определение. Множество называется ограниченым, если оно содержится в некотором шаре.

2.2.1. Является ли данное множество Т открытым, замкнутым, ограниченным в пространстве ? Найти его замыкание, внутренность и границу, проиллюстрировать ответ на чертеже (таблица 2.2.1).

Таблица 2.2.1

Вариант	Т	Вариант	Т
1		6
2		7
3		8
4		9
5		10

2.2.2. Является ли данное множество М открытым, замкнутым, ограниченным в пространстве ? Найти его замыкание, внутренние и граничные точки (таблица 2.2.2).

Таблица 2.2.2

Вариант	М	Вариант	М
1		6
2		7
3		8
4		9
5		10

2.2.3. Для данного множества А выяснить, является ли множество открытым, замкнутым, ограниченным в (таблица 2.2.3).

Таблица 2.2.3

Вариант		А	Вариант		А
1	1		6
2	2		7
3	2		8	2
4	5		9
5	3		10

Примеры решения типовых задач

1. Является ли данное множество Т открытым, замкнутым, ограниченным в пространстве ? Найти его замыкание, внутренность и границу, сделать чертеж.

Пример 1 .

Решение. Множество Т есть треугольник, ограниченный прямыми , у которого удалены стороны. Оно открыто. В самом деле, если точка а принадлежит Т, причем положительное число меньше расстояния от а до ближайшей стороны треугольника Т, то . Следовательно, . Далее, присоединяя к множеству Т все его точки прикосновения, получим, что замыкание Т есть треугольник

(объясните, почему). Следовательно, Т не замкнуто, и есть объединение сторон этого треугольника. Наконец, очевидно, что множество Т ограничено. Выполнение чертежа оставляем читателю.

2. Является ли данное множество открытым, замкнутым, ограниченным в пространстве ? Найти его замыкание, внутренние и граничные точки.

Пример 1. .

Решение. Множество М не является открытым, и более того, ни одна его точка не является внутренней. Действительно, для любой и для любого шара имеем , но , так как . Следовательно, .

Множество М является замкнутым, так как оно содержит все свои точки прикосновения. Действительно, пусть есть точка прикосновения множества М. Тогда в для некоторой последовательности . Но равенства влекут (почему?). А это значит, что .

Граница множества совпадает с самим множеством М, что теперь сразу следует из формулы .

Множество М не является ограниченным, так как, например, после-довательность принадлежит М, но

.

Пример 2. .

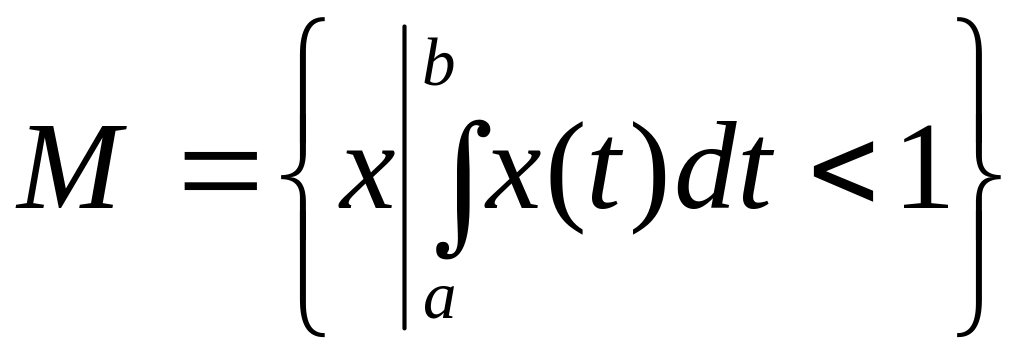Решение. Покажем, что М является открытым. Возьмём произвольную точку . Так как , то найдется такое , что 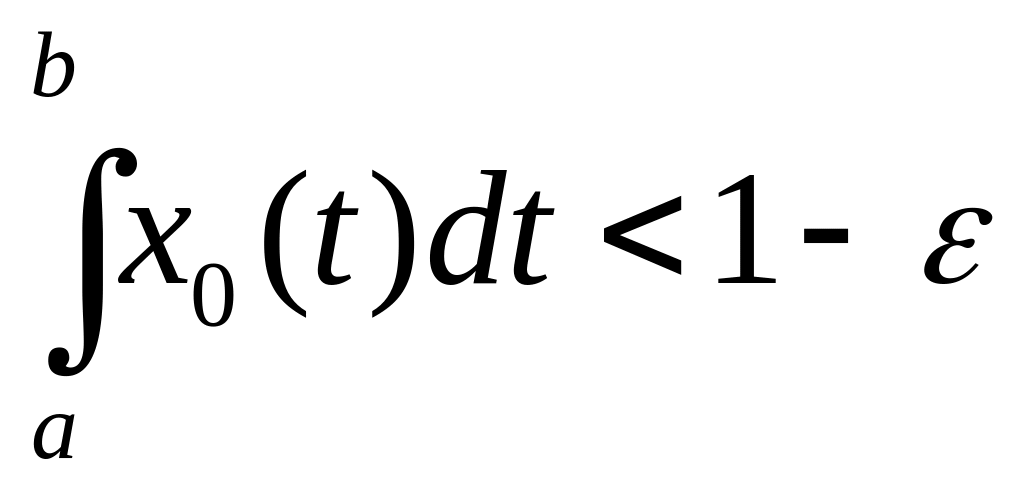. Покажем, что . В самом деле, для любого справедливо неравенство

.

Поэтому

.

Значит, .

Так как М открыто, то .

Множество М не является замкнутым, так как содержит не все свои точки прикосновения. Действительно, возьмём последовательность точек из М. Тогда , но 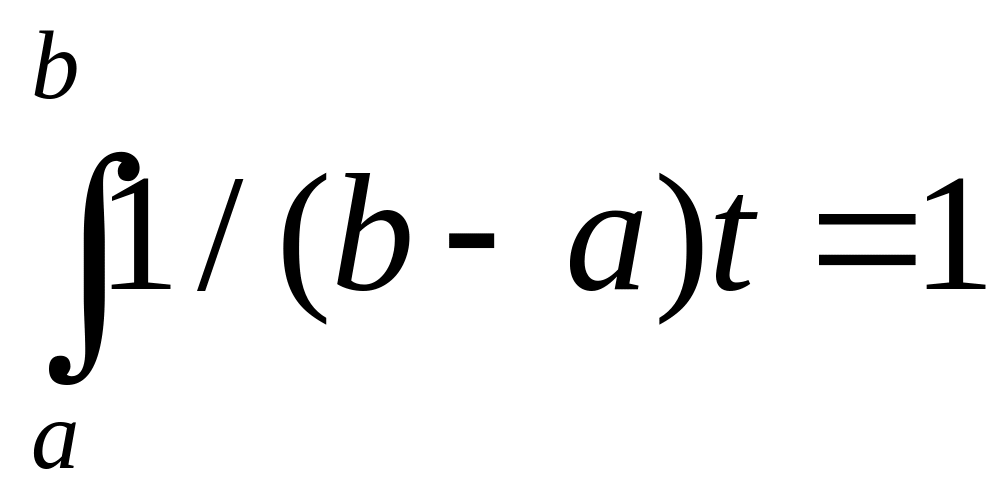, т.е. постоянная функция не принадлежит М.

Замечание. Так как любые две точки можно связать непрерывным путем , лежащим в , то пространство (и вообще любое нормированное пространство) всегда связно, и поэтому в нем нет открытых и одновременно замкнутых собственных подмножеств.

Теперь покажем, что 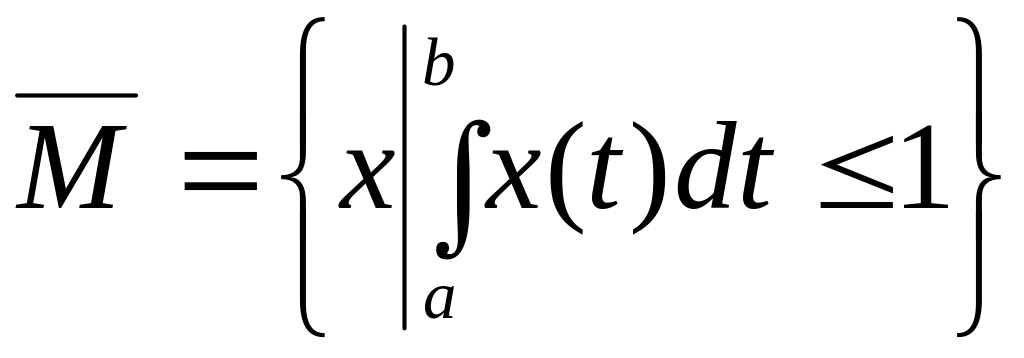. Действительно, если принадлежит , то найдется последовательность , равномерно сходящаяся к на . А тогда

.

Обратно, если , то последовательность принадлежит М и сходится к равномерно (проверьте!), а потому принадлежит .

Теперь ясно, что

.

Наконец, М не является ограниченным, так как, наприммер, последовательность постоянных функций принадлежит М, но .

Пример 3. .

Решение. Покажем, что М открыто. Пусть . Тогда , а потому для некоторого . Для любого имеем , и следовательно,

,

т. е. . Таким образом, точка x₀ – внутренняя для М.

Покажем, что

.

Действительно, если принадлежит , то найдется последовательность , равномерно сходящаяся к на . А тогда , т. е. принадлежит М.

Обратно, если , то последовательность принадлежит М и сходится к равномерно на (проверьте), а потому принадлежит .

Теперь ясно, что

.

Очевидно, что данное множество ограничено.

3. Для данного множества А выяснить, является ли множество открытым, замкнутым, ограниченным в .

Пример 1. .

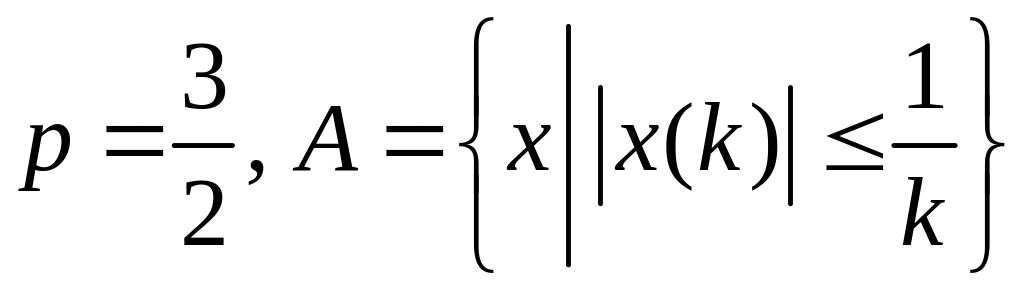Решение. Множество замкнуто, так как содержит в себе все свои точки прикосновения. Действительно, если есть точка прикосновения множества В, то найдется такая последовательность что в . Отсюда следует, что при всех имеем (почему?). Но так как , то и . Значит, .

Так как замкнуто, то оно не является открытым, поскольку пространство связно (см. замечание к примеру 2 в задаче 1). Но легко дать и прямое доказательство. Действительно, точка принадлежит , но для любого точка не принадлежит В, хотя и лежит в -окрестности точки . Следовательно, точка не является внутренней для В.

Наконец, ограничено, так как при всех из множества В справедливо неравенство

.

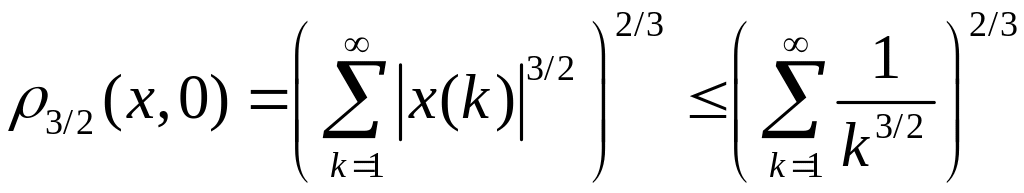Пример 2. .

Решение. Множество не является открытым. Для доказательства покажем, что точка не является для него внутренней. Возьмём и найдём такое натуральное N, что . Тогда

,

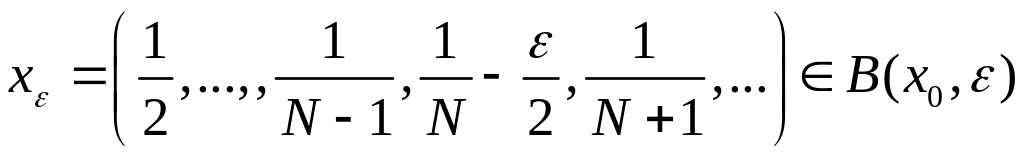но , поскольку .

Множество не замкнуто. Действительно, рассмотрим последовательность . Тогда сходится к точке , так как при , но .

Множество ограничено, так как при всех из В.

Пример 3. .

Решение. Покажем, что множество открыто.

Для любого элемента найдется такое , что

.

Если (шар рассматривается, конечно, в ), то

.

Тогда и

.

Теперь в силу неравенства Минковского имеем

.

Значит, , т. е. . Итак, .

Так как открыто, то не замкнуто по замечанию из решения примера 2 к задаче 1. Дадим прямое доказательство этого факта. Точки , где , очевидно, принадлежат . Но в то же время сходится в к .

Покажем, что не ограничено. Рассмотрим последовательность

.

Имеем , так как

,

но в то же время

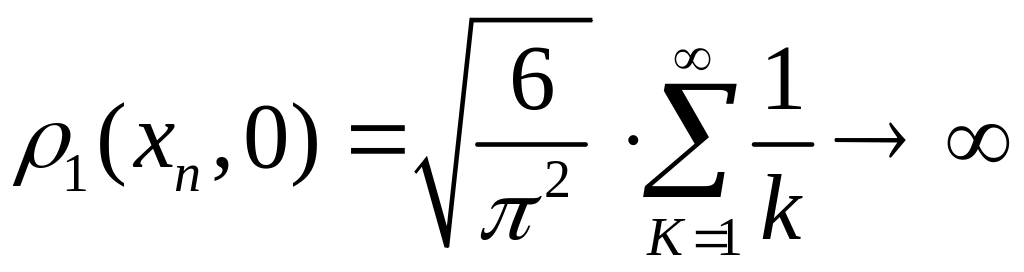при .

Пример 4. .

Решение. Покажем, что не является открытым. Возьмём и . Найдётся такое натуральное , что . Тогда , но .

Множество не является и замкнутым. Для доказательства рассмотрим последовательность

.

Она сходится к точке

,

которая не принадлежит , так как

.

Множество ограничено, поскольку неравенство влечет оценку

.
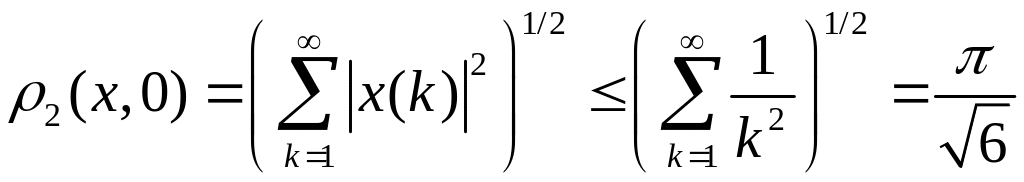