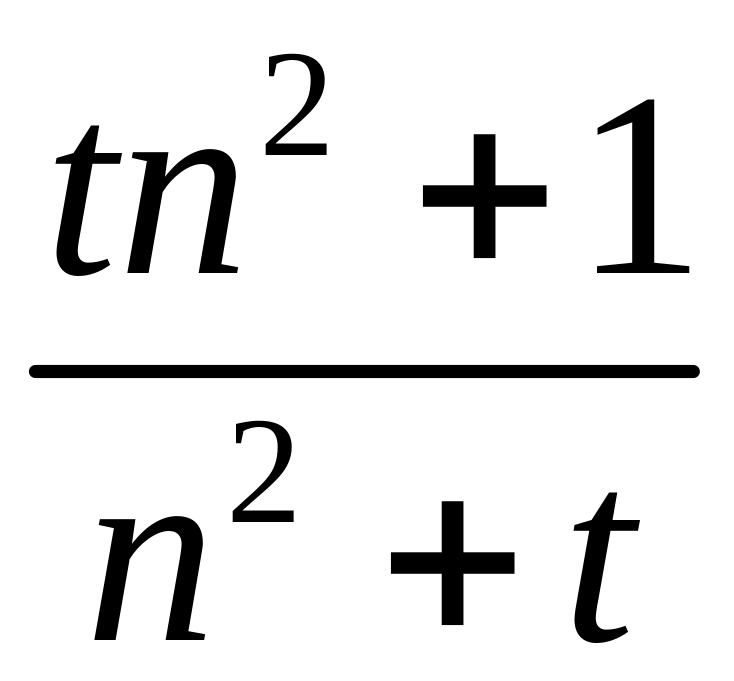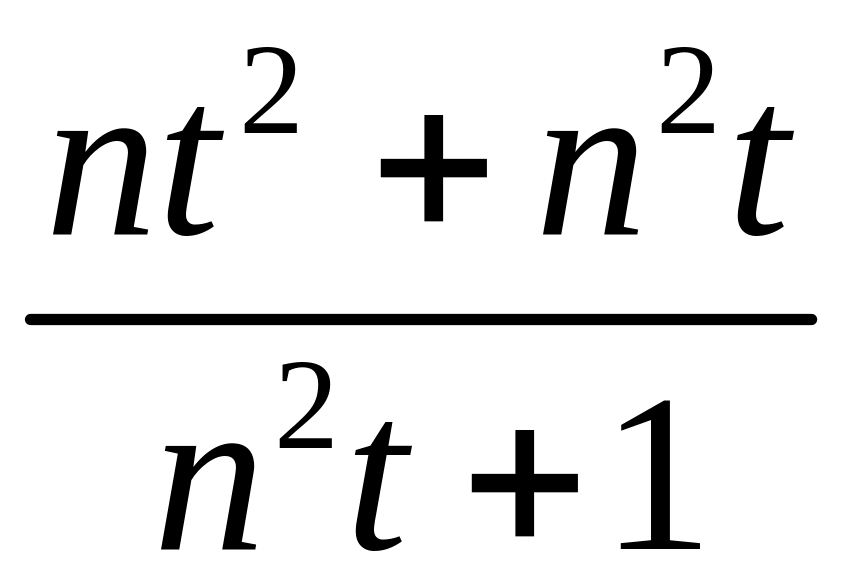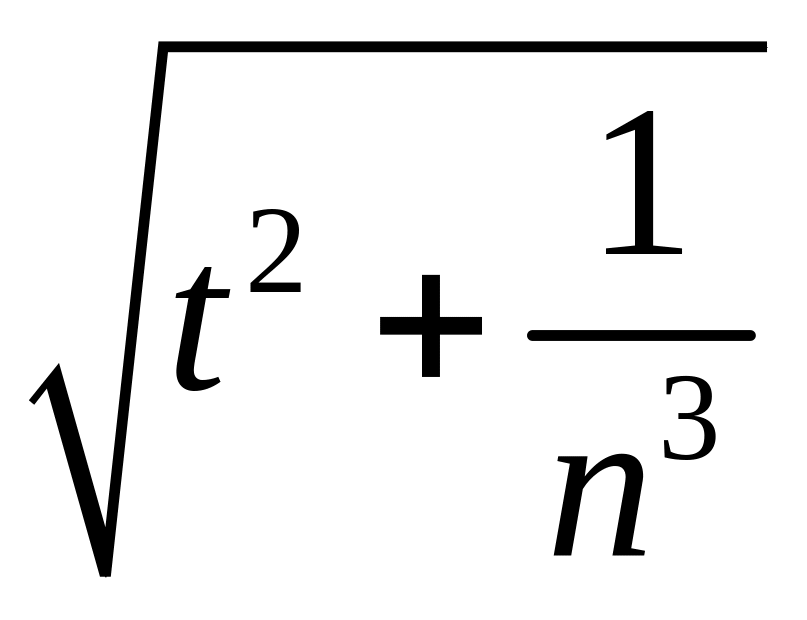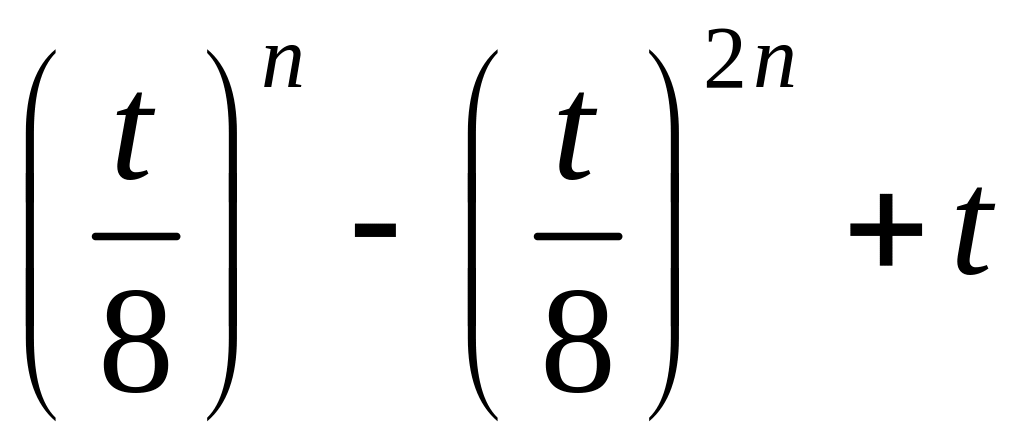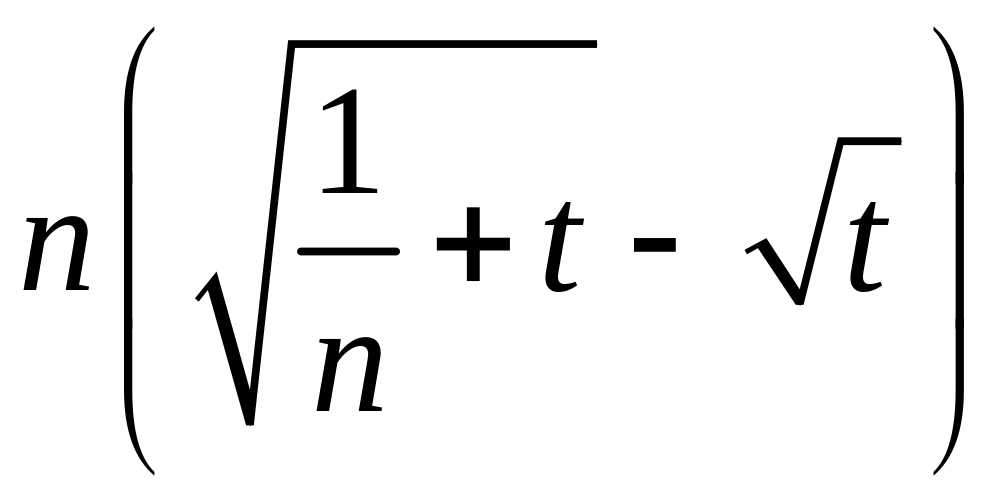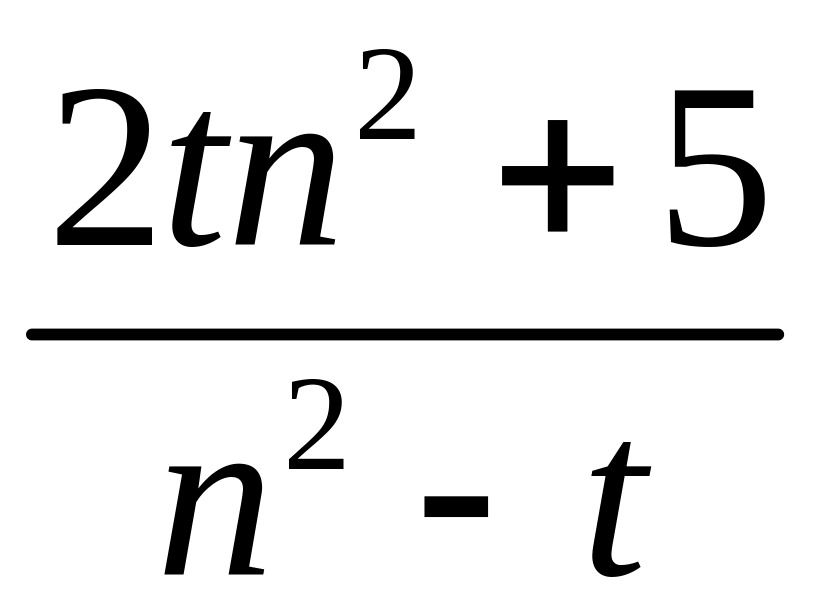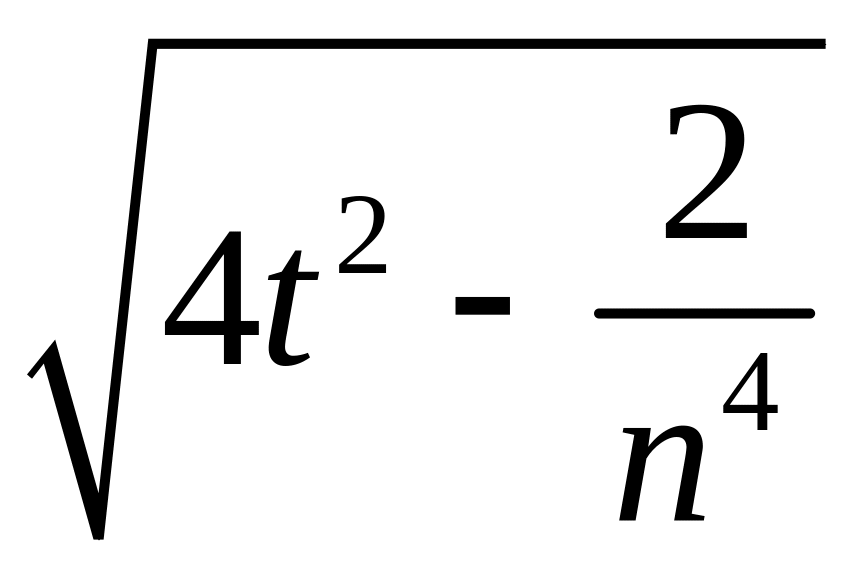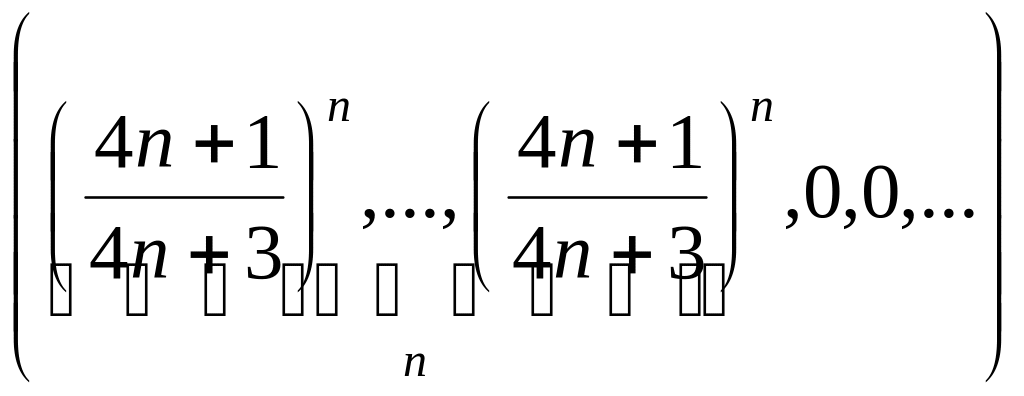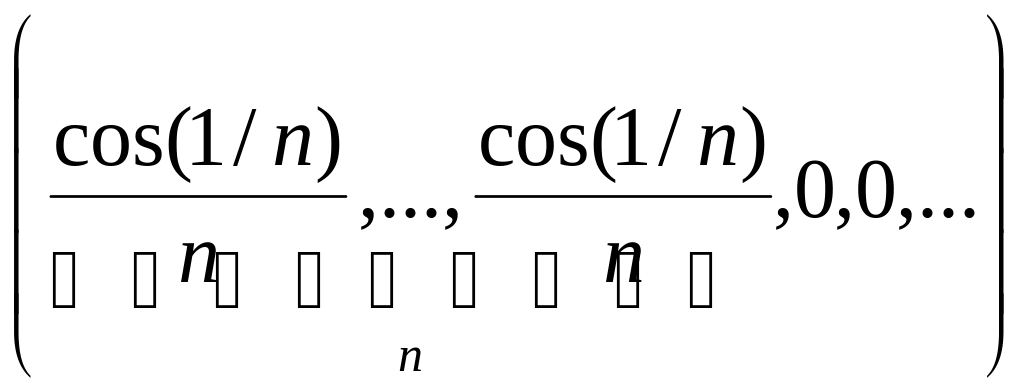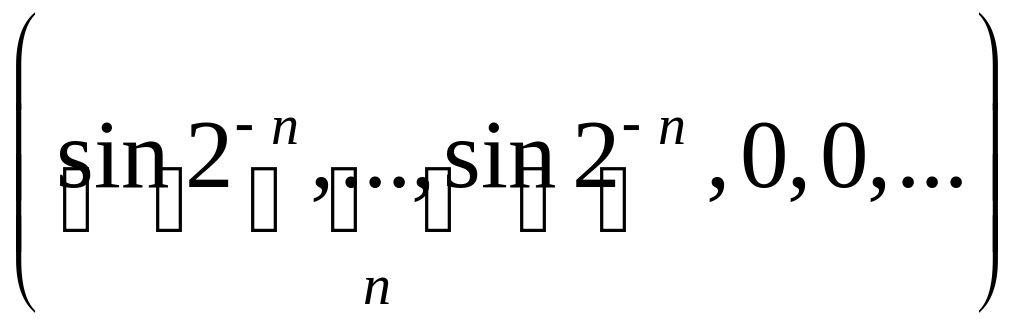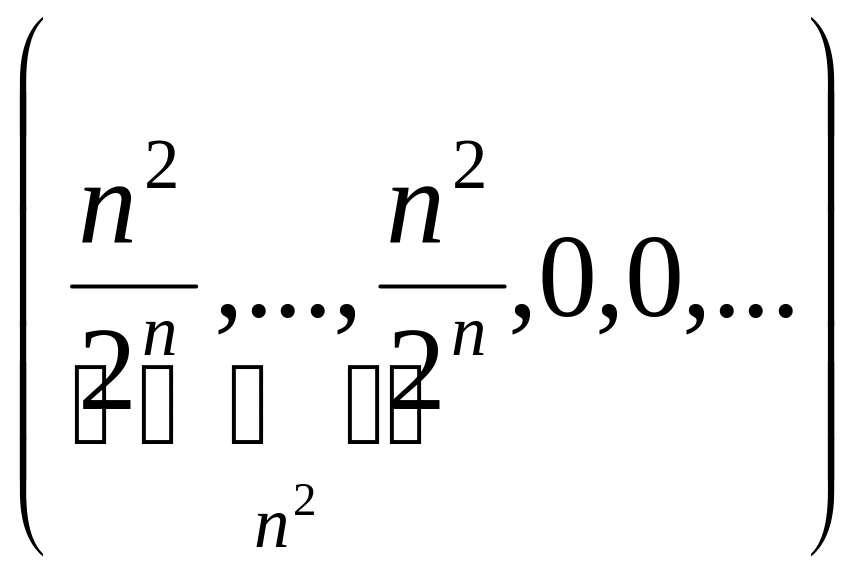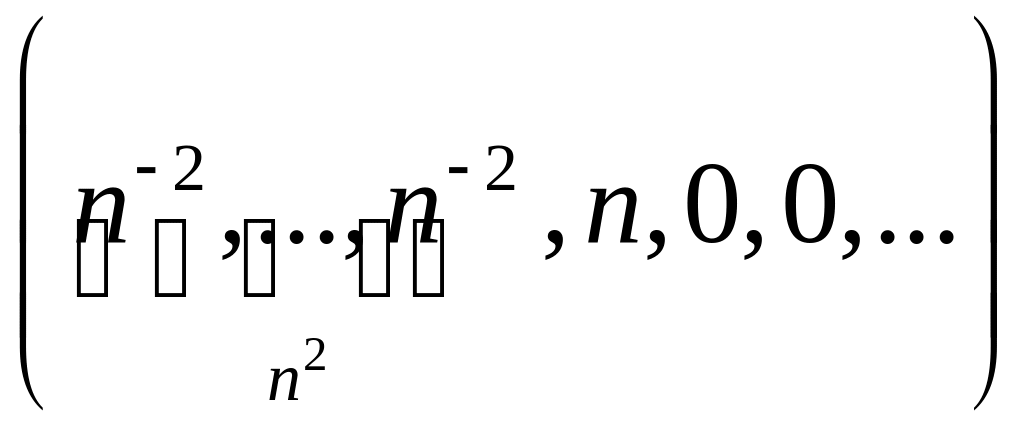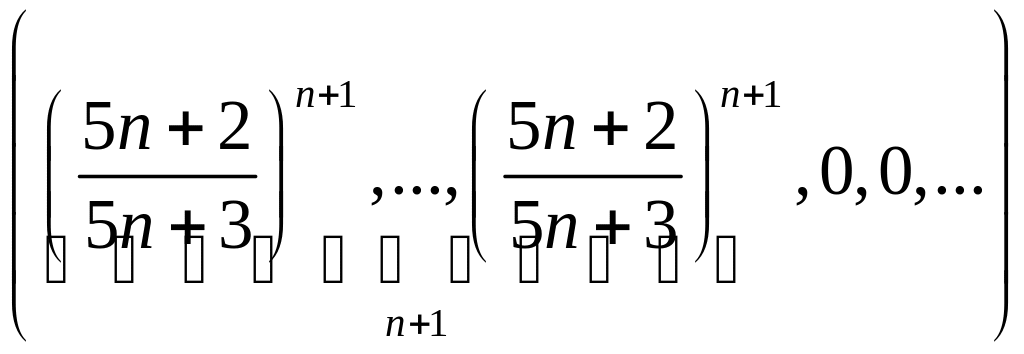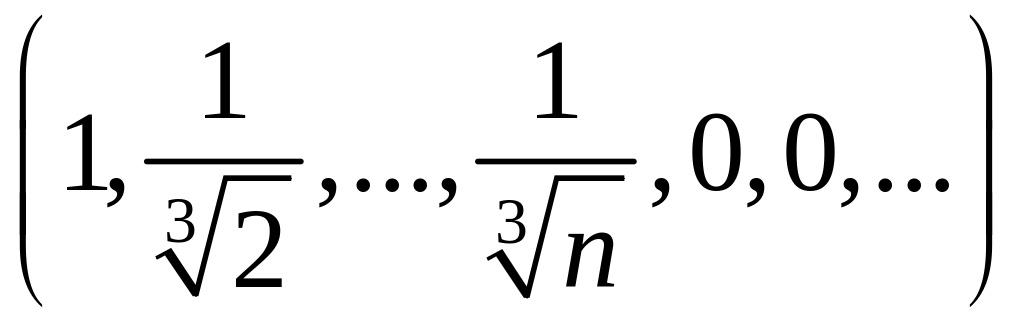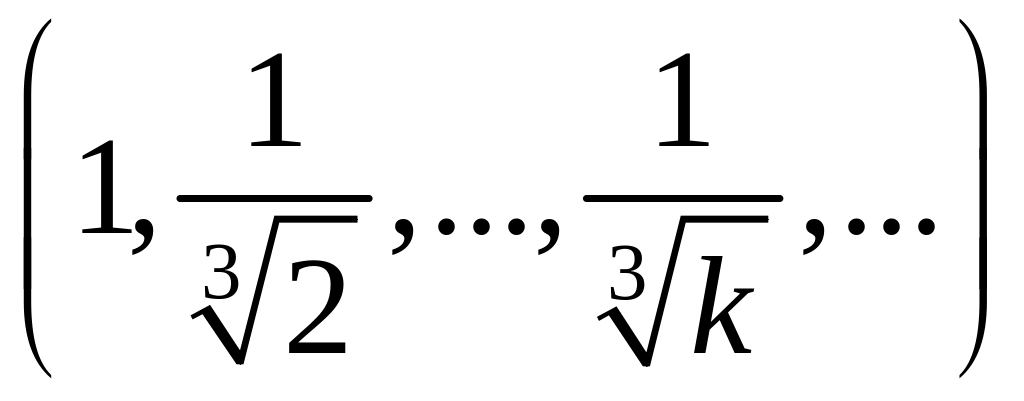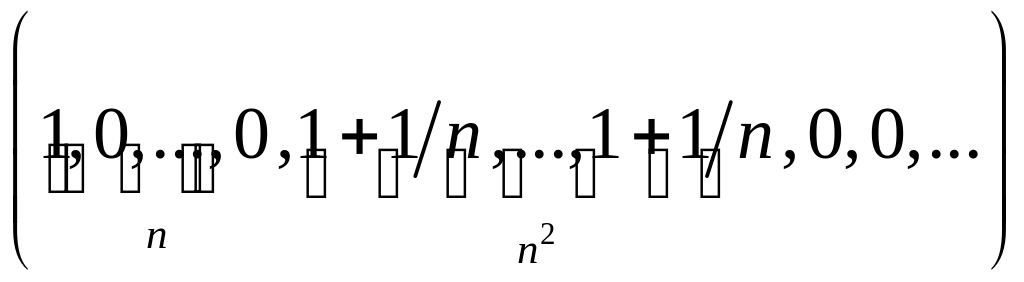2 Метрические пространства

Тема 2.1

Сходящиеся последовательности в метрических

пространствах

Определение. Пусть – непустое множество. Отображение , удовлетворяющее следующим условиям:

1)

2)

3)

называется метрикой на Х.

Множество Х, наделенное метрикой, т.е. пара , называется метрическим пространством.

Определение. Если же отображение удовлетворяет лишь условиям

)

2)

3)

то оно называется полуметрикой.

Определение. Пусть - метрическое пространство, - последовательность точек из Х, . Говорят, что стремится к а, (и пишут , или ) если

.

В этом случае а называют пределом последовательности , а сама эта последовательность называется сходящейся.

2.1.1. Является ли данная функция

а) полуметрикой;

б) метрикой на данном множестве Х (таблица 2.1.1.)?

Таблица 2.1.1

Вариант	Х
1
2
3
4
5
6
7
8
9
10

2.1.2. Проверить, сходится ли заданная последовательность x_n точек метрического пространства X к точке a, если выполнены следующие условия (таблица 2.1.2.)

Таблица 2.1.2

Вариант
1	2	3	4
1
2
3
4
5

Окончание таблицы 2.1.2

1	2	3	4
6
7			2
8
9			-
10

2.1.3. Проверить, сходится ли заданная последовательность xn точек метрического пространства X к точке a, если выполнены следующие условия (таблица 2.1.3).

Таблица 2.1.3

Вариант	X
1	2	3	4
1
2
3
4

Окончание таблицы 2.1.3

1	2	3	4
5
6
7
8
9
10