Тема 4.3

Компактные операторы

Всюду ниже X,Y,Z – нормированные пространства над полем К ( ), - линейный оператор.

Определение. Оператор А называется компактным, если он переводит ограниченные множества в предкомпактные.

Множество всех компактных операторов обозначается .

Каждый компактный оператор ограничен, но обратное, вообще говоря, неверно.

Теорема (свойства компактных операторов).

1) Множество есть замкнутое по норме подпространство пространства .

2) Пусть . Если один из операторов А или В компактен, то компактно и произведение АВ.

Определение. Оператор А называется оператором конечного ранга, если его образ есть конечномерное пространство.

Теорема. Ограниченный оператор конечного ранга компактен.

Теорема. Интегральный оператор Фредгольма компактен в пространстве .

4.3.1. Выяснить, является ли данный оператор компактным в пространстве (таблица 4.3.1).

Таблица 4.3.1

Вариант	А	Вариант	А
1		6
2		7
3		8
4		9
5		10

4.3.2. Определить, является ли данный оператор компактным в пространстве (таблица 4.3.2).

Таблица 4.3.2

Вариант	А
1
2
3
4
5
6
7
8
9
10

4.3.3. Исследовать оператор на компактность в пространстве (таблица 4.3.3).

Таблица 4.3.3

Вариант	А	Вариант	А
1	2	3	4
1		6
2		7

Окончание таблицы 4.3.3

1	2	3	4
3		8
4		9
5		10

4.3.4. Выяснить, является ли оператор компактным (таблица 4.3.4).

Таблица 4.3.4

Вариант	X	Y	А
1
2
3
4
5
6
7
8
9
10

Примеры решения типовых задач

1. Выяснить, являются ли следующие операторы компактными в пространстве .

Пример 1. .

Решение. Докажем, что данный оператор не является компактным. Возьмем множество . Оно ограничено в . В то же время множество не является предкомпактным в , так как не удовлетворяет свойству Больцано-Вейерштрасса. В самом деле, из последовательности нельзя извлечь сходящуюся в подпоследовательность в силу того, что любая ее подпоследовательность будет иметь разрывный предел (какой?), а предел равномерно сходящейся последовательности непрерывных функций должен быть непрерывен. В соответствии с определением компактного оператора данный оператор не компактен.

Пример 2. .

Решение. Представим данный оператор в виде , где

, ,

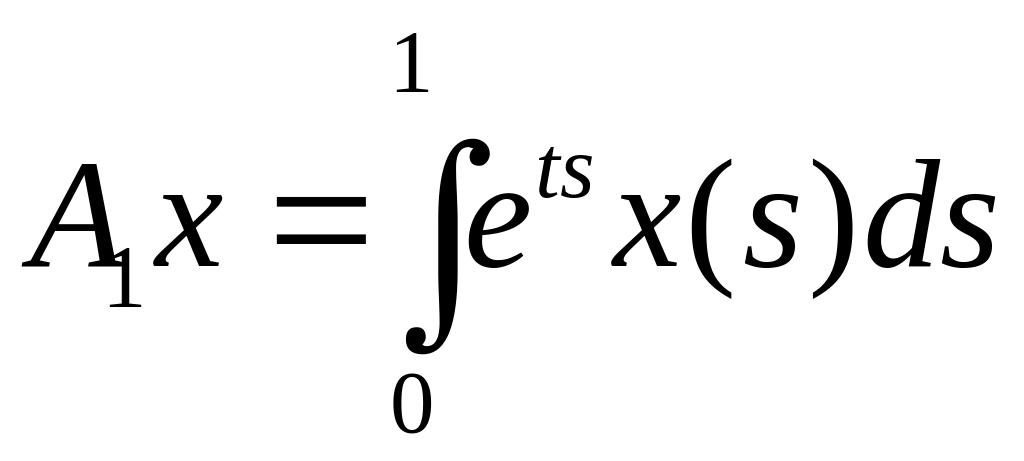и докажем, что операторы и компактны. Оператор компактен как интегральный оператор Фредгольма с непрерывным ядром. Компактность оператора следует из того, что он является ограниченным оператором конечного ранга. Действительно, он ограничен, так как

,

а с другой стороны образ оператора А есть

,

а потому

_,

поскольку все функции линейно выражаются через функцию . Следовательно, оператор компактен как сумма компактных операторов.

2. Выяснить, является ли оператор компактным.

Пример 1. .

Решение. Докажем, что оператор является компактным. Рассмотрим следующую последовательность линейных операторов конечного ранга:

(образ оператора содержится в n-мерном подпространстве пространства l₁ , состоящем из векторов вида ).

Эти операторы ограничены. Действительно,

Следовательно, они компактны. Теперь компактность оператора А следует из того, что последовательность сходится к А по норме, так как

,

а потому

_,

поскольку остаток сходящегося ряда стремиться к нулю.

3. Выяснить, является ли оператор компактным.

Пример 1. _, .

Решение. Возьмем в произвольное ограниченное множество М. Его ограниченность означает, что

.

Отсюда следует, что

, .

Рассмотрим теперь множество . Оно равномерно ограничено, так как . Кроме того, равностепенно непрерывно, так как по теореме Лагранжа

.

В силу теоремы Арцела-Асколи множество предкомпактно. Значит, оператор А компактен.

Пример 2. _, .

Решение. Возьмем ограниченное в множество

(проверьте ограниченность множества М). Множество не является предкомпактным в пространстве _, так как не содержит сходящихся в подпоследовательностей (т. е. не удовлетворяет свойству Больцано-Вейерштрасса). В самом деле, из сходимости последовательности в следует равномерная сходимость последовательности ее производных (проверьте это). А с другой стороны, из последовательности нельзя извлечь равномерно сходящуюся подпоследовательность (почему?). Значит, данный оператор не компактен.