3.5Упругий и неупругий удары

Удар (или соударение) — это стол­кновение двух или более тел, при кото­ром взаимодействие длится очень ко­роткое время. Силы взаимодействия между стал­кивающимися телами (ударные или мгновенные силы) столь велики, что вне­шними силами, действующими на них, можно пренебречь. Это позволяет сис­тему тел в процессе их соударения при­ближенно рассматривать как замкну­тую систему и применять к ней законы сохранения.

Твёрдые тела при столкновениях подвергаются деформациям, между сталкивающимися телами происходит обмен энергией и импульсом. Некоторая часть первоначальной энергии переходит в потенциальную энергию упругих деформаций, возбуждение колебаний и волн, а так же на совершение работы против сил внутреннего трения. Другая часть энергии расходуется на увеличение внутренней энергии тела, т.е. на увеличение температуры.

Плоскость контакта называется плоскостью удара, а прямую, ей перпендикулярную и пересекающую ее в точке соприкосновения, называют линией удара. Если линия удара параллельна скоростям сталкивающихся тел, удар называется прямым; если эта линия проходит через центры сталкивающихся тел, удар называют центральным. При исследованиях явлений столкновения тел важное значение имеют законы сохранения импульса и механической энергии.

Существуют два предельных вида удара: абсолютно неупругий и аб­солютно упругий.Абсолютно упругимназывается такой удар, при кото­ром механическая энергия тел не переходит в другие, немеханические, ви­ды энергии. При таком ударе кинетическая энергия переходит полностью или частично в потенциальную энергию упругой деформации. Затем тела возвращаются к первоначальной форме, отталкивая друг друга. В итоге потенциальная энергия упругой деформации снова переходит в кинетиче­скую энергию, и тела разлетаются со скоростями, величина и направление которых определяются двумя условиями - сохранением полной механиче­ской энергии и сохранением полного импульса системы тел.

А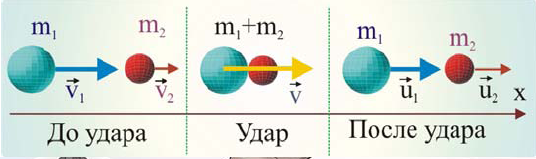 бсолютно неупругий удархарактеризуется тем, что потенциальной энергии деформации не возникает; кинетическая энергия тел полностью или частично превращается во внутреннюю энергию; после удара столк­нувшиеся тела либо движутся с одинаковой скоростью, либо покоятся. При абсолютно неупругом ударе выполняется лишь закон сохранения им­пульса, закон же сохранения механической энергии не соблюдается; имеет место закон сохранения суммарной (полной) энергии различных видов -механической и внутренней.

Рассмотрим вначале абсолютно упругое взаимодействие. Наиболее показательным примером, является центральный удар шаров, на которые не действуют внешние силы, в этом случае справедливы законы сохранения импульса и энергии. Пусть два абсолютно упругих шара массами и движутся до удара поступательно со скоростями и и после удара и

Требуется определить скорости шаров и после соударения. До удара шаров и после него они не деформированы, поэтому потенциальную энергию системы можно считать неизменной и равной нулю.Запишем уравнения законов сохранения энергии и импульса:

(1)

(2)

Пусть скорости шаров до удара направлены вдоль оси х, тогда уравнение закона сохранения импульса в скалярном виде будет иметь вид:

(3)

Умножим уравнение (2) на «2» и перенесем в уравнениях (2) и (3) в левую часть члены, относящиеся к первому телу, а в правую часть – ко второму телу:

Или

(4)

(5)

Разделим уравнение (5) на (4):

(6)

Выразим из (6) u₁и подставим в (3):

(7)

Аналогично из (6) u₂и подставим в (3):

(8)

Р ассмотрим теперь абсолютно неупругий удар двух частиц, обра­зующих замкнутую систему. Пусть массы частиц равны m₁ и m₂, а их ско­рости до удара и . В силу закона сохранения суммарный импульс частиц после удара должен быть таким же, как и до удара:

(9)

где - одинаковая для обеих частиц скорость после удара (частицы сли­паются).

Из (9) следует, что

(10)

Выясним, как изменяется кинетическая энергия шаров при центральном абсолютно неупругом ударе. Так как в процессе соударения шаров между ними действуют силы, зависящие не от самих деформаций, а от их скоростей, мы имеем дело с силами, подобны­ми силам трения, поэтому закон сохра­нения механической энергии не выполняется. Вследствие деформации происходит «потеря» кинетической энергии, перешедшей в тепловую энергию.

(11)

Рассмотрим частные случаи.

Пусть массы тел равны . Тогда после удара имеем ,

При абсолютно упругом соударении одинаковых тел они просто обмениваются скоростями. В частности, если на неподвижный бильярдный шар налетает другой шар, то налетающий шар останавливается, а покоящийся приобретает его скорость.

Другой частный случай - соударение тела с неподвижной стенкой (которую можно понимать как тело бесконечной массы), т. е. v₂ = О и т₂= ∞. После удара u₁ = - v_1, u₂ = 0.

Глава № 4 МЕХАНИКА ТВЕРДОГО ТЕЛА

ЛЕКЦИЯ № 6