3.3 Закон сохранения энергии

Сумма кинетической и потенциальной энергий называется полной энергией.

Пусть дана изолированная замкнутая система, состоящая из точек массами m₁, m₂, …m_n, движущихся со скоростями v₁, v₂, …v_nи взаимодействующих между собой.Тогда уравнение движения для каждой точки:

……………………………….

Домножим каждое уравнение на , учитывая

……………………………….

Так как получаем

………………..

Величину можно представить как , а тогда

……………………..

Или

– сумма - полная кинетическая энергия всех точек

– полная потенциальная энергия всех точек

(2.36)

З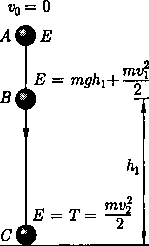 акон сохранения энергии: Для замкнутой изолированной системы, в которой действуют только консервативные силы, полная механическая энергия остается постоянной. Она переходит из одного вида в другой.

То, что полная энер­гия остается неизменной демон­стрируется на примере свободного па­дения тела без учета сопротив­ления среды. Этот закон не есть просто закон количественного сохранения энергии, а закон сохранения и превра­щения энергии, выражающий и каче­ственную сторону взаимного превраще­ния различных форм движения друг в друга.

3.4 Графическое представление энергии

В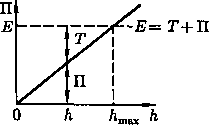 о многих задачах рассматривается одномерное движение тела, потенци­альная энергия которого является фун­кцией лишь одной переменной (например, координаты х), т.е. П = П(х). График зависимости потенциальной энер­гий от некоторого аргумента называетсяпотенциальной кривой.

Рассмот­рим графическое представление потен­циальной энергии для тела в однород­ном поле тяжести и для упругодеформированного тела. Потенциальная энергия тела массой m, поднятого на высотуh над поверхностью Земли . График данной зависимости П = П(h) — прямая линия, проходящая через нача­ло координат, угол наклона которой к оси hтем больше, чем боль­ше масса тела.

Пусть полная энергия тела равнаЕ(ее график — прямая, параллельная оси h). На высоте h тело обладает потен­циальной энергией П, которая опреде­ляется отрезком вертикали, заключен­ным между точкой hна оси абсцисс и графиком П(h). Естественно, что кине­тическая энергия Т задается ординатой между графиком П(h) и горизонтальной прямой ЕЕ. Из рис. следует, что если

h=h_max, то T=0 и П=E = mgh_maxт.е.

потенциальная энергия становится мак­симальной и равной полной энергии.

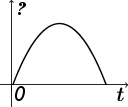
Тело брошено вертикально вверх с поверхности Земли. На каком из графиков показана зависимость потенциальной энергии взаимодействия тела с Землей от времени ? За нуль потенциальной энергии принять поверхность Земли.                1.                               2.                                      3.                      4.                                       

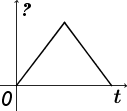
1. На первом

2. На втором

3. На третьем

4. На четвертом

З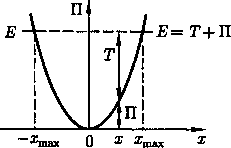 ависимость потенциальной энергии упругой деформации от дефор­мации х имеет вид параболы (рис.), где график заданной полной энергии тела Е — прямая, параллельная оси аб­сцисс x. Из рис. сле­дует, что с увеличением деформации х потенциальная энергия тела возраста­ет, а кинетическая — уменьшается. Аб­сцисса х_mах определяет максимально возможную деформацию растяжения тела, а -х_тах — максимально возмож­ную деформацию сжатия тела.

Из анализа графика на рис. выте­кает, что при полной энергии тела, рав­нойЕ, тело не может сместиться вправо от x_max и влево от -x_max, так как кинети­ческая энергия не может быть отрица­тельной и, следовательно, потенциаль­ная энергия не может быть больше пол­ной энергии. В таком случае говорят, что тело находится в потенциальной яме с координатами — x_max<х < х_maх.

Пусть в замкнутой системе действуют кроме консервативных сил F_i действуют диссипативные силы f_i, кроме того на систему действуют внешние силы Ф_i, тогда уравнение движения будет иметь вид:

Домножим на

(2.37)

Если в системе действуют диссипативные силы и кроме того на систему действуют внешние силы, то закон сохранения энергии не выполняется (энергия не остается постоянной величиной); энергия тратится на совершение работы против диссипативных и внешних сил.

Выражения (2.37) и (2.38) называются законам изменения механической энергии.

Коэффициентом полезного действия (КПД) называется отношение полезной (для какой-то практической цели) совершенной работы (энергии) ко всей работе, совершенной системой (к поступившей в систему энергии):

Закон сохранения механической энергии связан с однородностью времени. Однородность времени означает, что если в два любые момента времени все тела замкнутой системы поставить в совершенно одинаковые условия, то начиная с этих моментов все явления в ней будут протекать совершенно одинаково. Например, при свободном падении тела в поле сил тяжес­ти его скорость и пройденный путь за­висят лишь от начальной скорости и продолжительности свободного паде­ния тела и не зависят от того, когда тело начало падать.