3.2 Кинетическая и потенциальная энергии

Единой мерой различных форм движения служит физическая величина, называемая энергией. С различными формами движения материи связывают различные формы энергии: механическую, тепловую, электромагнитную, ядерную и др.

Механическая энергия – это мера движения и взаимодействия тел.Кинетическая энергия – это запас той работы, которую может совершить тело за счет своего движения.

Согласно закону Ньютона:

или

домножим обе части равенства на перемещение

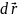
так как

то

Если тело изменяет свою скорость от v₀до v, то

(2.27)

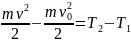
Если ,

(2.28)

Данная физическая величина называется кинетической энергией тела. Т.о. кинетическая энергия характеризует движение тела.

Работа результирующей силы, действующих на тело, равна изменению кинетической энергии:

. (2.29)

П остоянное силовое поле обладает следующим свойством: если в таком поле материальная точка движется по замкнутому пути (так что в результате движения точка возвращается в исходное положение), то работа, совершаемая при этом силами поля, будет равна нулю. Силы, которые удовлетворяют этому свойству, называют консервативными. Силы, работа которых удовлетворяет этому свойству, называются консервативными. Из этого свойства следует и другое утверждение: работа консервативных сил при переносе частицы из одного положения в другое не зависит от вида пути, по ко­торому происходит перенос, а определяется только положением (коор­динатами) начальной и конечной точек переноса. К консервативным силам относятся: сила гравитации, сила упругости, сила кулона.

Действительно, рассмотрим две точки 1 и 2 и соединим их двумя кривыми а и b (рис.). Предпо­ложим, что частица, находящаяся в силовом поле, переводится из точки 1 в точку 2 вдоль кривой а и затем из точки 2 назад в точку 1 по кривой b. Общая работа, которая производится при этом силами поля, равна нулю:

А_1а2 + А_2b1 = 0.

При изменении направления переноса на обратное работа меняет знак (си­ла постоянна, а перемещение меняет знак). Поэтому следует, что

A_1a2 = - A_2b1 ,

т. е. работа не зависит от вида кривой, а зависит от перемещения, соединяющего начальную и конеч­ную точки перехода 1 и 2.

Силы, работа, которых по замкнутой траектории не равна нулю, называются диссипативными (неконсервативными). Например, сила трения, её работа всегда отрицательная.

Потенциальная энергия– это запас той работы, которую может совершить тело за счет изменения места положения в пространстве.

Потенциальная энергия определяется через работу: работа консервативных сил при бесконечно малом изменении конфигурации системы равна приращению потенциальной энергии, взятому со знаком «-»

Работа совершается за счет убыли потенциальной энергии:

(2.30)

П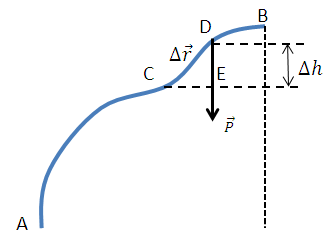 отенциальная энергия в отличии от кинетической энергии не имеет универсальной формулы. Для каждой потенциальной силы будет своё аналитическое выражение.

1. Пусть тело массой m перемещается из точки А в точку В.

Из точки С в точку D совершается работа, которая равна:

Из ΔСВE

Тогда

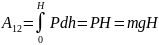(2.31)

При сравнении (2.30) и (2.31) получим формулу для потенциальной энергии силы тяжести:

(2.32)

2. О 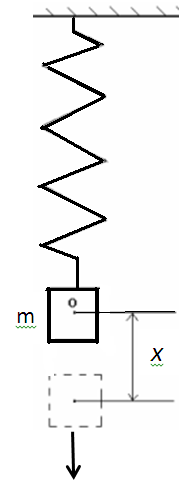пределим потенциальную энергию для силы упругости. Пусть дан груз массой m, если отвести груз от положения равновесия на расстояние х , то тело возвращается обратно под действием силы упругости , где k- жесткость пружины.

Рассчитаем элементарную работу

Или

Полная работа при изменении пружины равна

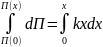
(2.33)

3. Как и всякие другие сила тяготения при движении тела способна совершать работу. Силы тяготения являются потенциальными силами, т.е. работа этих сил не зависит от вида траектории движения, а определяется положением начальной и конечной точки перемещения. Если взаимодействуют два тела массами m₁ и m_2, то работу на элементарном перемещении можно представить следующим образом

(15)

знак минус показывает, что перемещение направлено в сторону противоположную направлению силы тяготения. Работа на конечном перемещении определится как

(16) .

Так как , то изменение потенциальной энергии

(17)

Удобно принять, чтобы на больших расстояниях потенциальная энергия (энергия взаимодействия) стремилась к нулю:

Тогда имеем

Связь потенциальной энергии с консервативными силами:

(2.34)