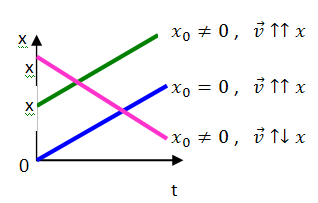Физические основы механики

Глава № 1. Кинематика

ЛЕКЦИЯ 1, 2

Тема: Механическое движение. Скорость.

1.1 Введение

Физика – это наука о природе. Она возникла из стремления понять и описать окружающий нас мир. Мир наш необычайно сложен и интересен: Солнце, Луна, приливы, отливы, землетрясения, день, ночь, море, облака, горы, ветер, животный и растительный мир. Человек – часть этого мира пытается понять как устроен он. Возможно ли это? Из нашего общего опыта мы знаем, что мир познаваем и что многое известно о физических законах, которые приводят к тому многообразию явлений, которые окружают нас. Физические законы образуются в результате обобщения экспериментальных данных и выражают объективные закономерности, существующие в природе.

Физика – это раздел естествознания, который изучает наиболее общие свойства и формы материи. Материя – это философская категория, изображающая объективную реальность, существующую вне сознания человека, которая отображается, копируется, фотографируется чувствами человека и существует независимо от них.

Известно два вида материи: веществои поле. К веществу относятся, например, атомы, молекулы, и все построенные из них тела. Второй вид материи образуют электромагнитные, гравитационные поля. Эти виды материи неразрывно связаны друг с другом и могут превращаться друг в друга. Например, электрон и позитрон (представляют собой вещество) могут превращаться в фотоны (т.е. электромагнитное поле).

Механика – раздел физики, изучающий наиболее простое движение материи. Движение материи происходит в пространстве и времени, т.о. пространство и время – формы существования материи.

1.2 Механическое движение. Система отсчета. Кинематические уравнения движения

Что такое движение и как его описать? На этот вопрос отвечает кинематика, описывающая движение тел.

Механическое движение – это изменение положения тел или их частей в пространстве с течением времени относительно друг друга. Тело, по отношению к которому рассматривается движение какого-то другого тела, называется тело отсчета.

Д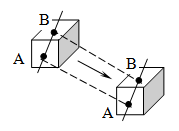 вижение тел принято разделять на несколь­ко простых видов: поступательное, вращатель­ное и колебательное.

При поступательном движении прямая, соединяющая две произвольные точки тела, перено­сится параллельно себе самой. Для изучения поступательного движения тела достаточно изучить движение какой-либо одной из его то­чек, т. к. все точки тела движутся совершенно одинаково.

П ри вращательном движении тела все его точки описывают окружности в параллельных плоскостях, причем центры этих окружностей лежат на одной прямой, называемой осью вра­щения.

Колебаниями называются движения, повторяю­щиеся во времени, в окрестности некоторого поло­жения равновесия. Например, если мы подтолкнем шарик, висящий на ни­ти, то он будет совершать колебания около своего первоначального отвесного положения.

Изучение поведения тел в механике основано на двух основных моделях тел: материальной точке и абсолютно твердом теле.

Тело, размерами которого в условиях данной задачи можно пренебречь, называется материальной точкой.

Тело, конечных размеров называется абсолютно твердым, если в ус­ловиях данной задачи можно пренебречь его деформацией.

Для описания положения материальной точки вводится система координат. Совокупность тела отсчета, системы координат и часов, отсчитывающих время, называется системой отсчета. Число независимых движений, которые может совершать тело, называют числом степеней свободы. Число степени свободы – это число, которое можно задать для описания положения тел системы. Например, материальная точка имеет три степени свободы если она двигается в пространстве: поступательное движение вдоль оси x, y, z; при движении на плоскости достаточно две координатные оси, следовательно в этом случае число степеней свободы равно двум, а при движении вдоль прямой – число степеней свободы равно одному.Абсолютно твердое тело может обладать тремя степенями свободы поступательного движения, тремя степенями свободы вращательного движения, если тело не абсолютно твердое и его части могут смещаться друг относительно друга, то необходимо вводить еще дополнительные три степени свободы колебательного движения.

Выбор системы отсчета позволяет описать движение рассматривае­мых тел. Координаты – это функции времени:

x(t) = x; y(t) = y; z(t) = z (1.1)

У 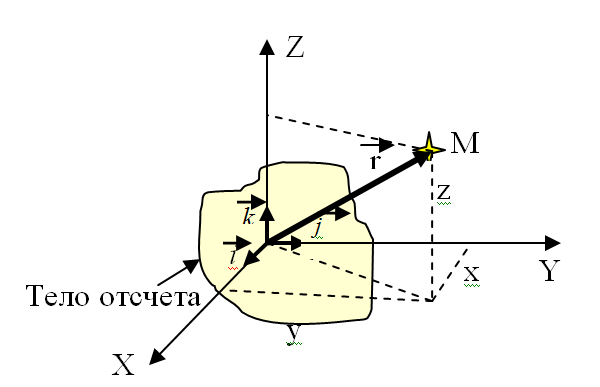равнения (1), с помощью которых можно предсказывать положение точки, называется кинематическим уравнениемдвижениятела.

Если указать не только начальное положение точки, но и указать направление движения, то задача упрощается (вместо трех уравнений – получится одно уравнение):

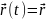(1.2),

где 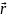- радиус вектор, проведенный из начала координат в точку М.

Уравнения (1) и (2) равносильны. Если ввести единичные векторы характеризующие направление осей координат, то положение точки можно выразить через данные вектора.

Свойства векторов:

, ,

Сумма трех векторов: равна радиус-вектору :

(1.3)

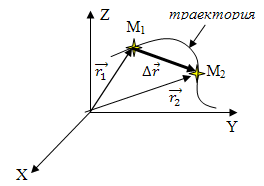
Линия, описывающая движение тела, называется траекторией. Длина траектории от точки М₁до точки М₂ – это путь. Путь – это скалярная физическая величина равная сумме длин отрезков траектории. Вектор, соединяющий начальное положение тела с конечным, называется перемещением .

Модуль малого приращения равен длине соответствующей ему дуги траектории:

или

В зависимости от формы траектории различают прямолинейное и криволинейное движения точки.

1.3 Скорость

Для характеристики движения материальной точки вводят векторную физическую величину – скорость.

Пусть материальная точка движется по криволинейной траектории так, что в момент t₁ она находилась в точке М₁, а в момент времени в точке М₂

При движении материальной точки относительно системы отсчета меняется направление перемещения:

Время, потраченное на перемещение :

Вектором средней скорости называют отношение приращения радиус-вектора точки за интервал времени Δ t к его величине:

(1.4)

Если известно и , то можно найти перемещение точки:

Вектор средней скорости характеризует только быстроту движения материальной точки за минимальный промежуток времени. Направление вектора совпадает с направлением перемещения . Если в выражении (1.4) перейти к пределу, устремляя к нулю, то получим выражение для мгновенной скорости:

(1.5)

По мере уменьшения длина пути все больше будет приближаться к модулю радиус-вектору , поэтому модуль мгновенной скорости

(1.6)

Если за произвольные равные промежутки времени точка проходит пути разной длины, то численное значение ее мгновенной скорости с течением времени изменяется. Такое движение называют неравномерным движением. В этом случае пользуются скалярной величиной , называемой средней путевой скоростью. Она равна отношению пройденного пути к интервалу времени, в течение которого был совершен этот путь:

(1.7)

Если численное значение мгновенной скорости остается во время движения точки неизменным, то такое движение называют равномерным.

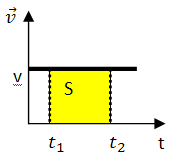
Длина пути, пройденного точкой за время :

(1.8)

П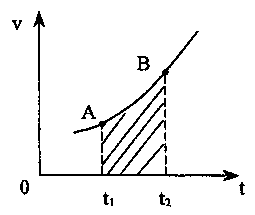 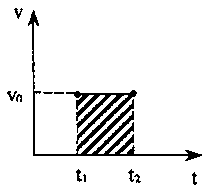уть равен площади криволинейной фигуры в случае неравномерного движения и площади прямоугольника, при равномерном движении.

1.4 Ускорение.

При движении материальной точки её скорость может непрерывно меняться как по величине (модулю), так и по направлению.

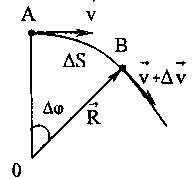
Пусть за время движущаяся точка перешла из положенияА в положение В, и вектор ее скорости 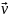изменился на , тогда отношение вектора к называется средним ускорением неравномерного движения:

(1.9)

Ускорением или мгновенным ускорением, точки в момент времени t называют векторную величину , равную пределу, к которому стремиться среднее ускорение этой точки в промежуток времени от tдо при неограниченном уменьшении

(1.10)

Ускорение измеряется в м/с².

Ускорение, характеризующее изменение скорости по модулю, называется тангенциальным ускорением:

(1.11)

Таким образом, тангенциальная составляющая ускорения описывает изменение модуля скорости и направлена вдоль скорости, т. е. по касательной к траектории.

Ускорение, характеризующее изменение скорости по модулю, называется тангенциальным ускорением.Нормальная составляющая ускорения возникает только при криво­линейном движении.

(1.12)

Величину R называют радиусом кривизны траектории.. В частном случае вектор нормального ускорения направлен к центру и называется центростремительным.

П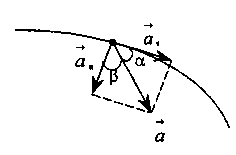 олное ускорение равно сумме тангенциального и нормального ускорений:

(1.13)

Тангенциальное и нормальное ускорения взаимно перпендикулярны между собой, поэтому модуль полного ускорения:

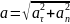(1.14)

1. Равномерное прямолинейное движение.. Это движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещения.

(скорость по направлению и модулю остается постоянной) При равномерном прямолинейном движении полное перемещение равно пройденному пути Кинематическое уравнение движения:

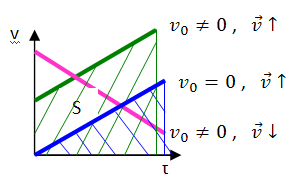
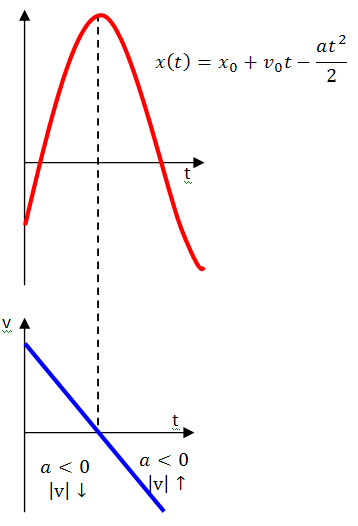
2. Неравномерное прямолинейное движение. Это движение, при котором направление скорости остается постоянным, а модуль изменяется.

Полное ускорение Скорость При равномерном прямолинейном движении полное перемещение равно пройденному пути Кинематическое уравнение движения:

3. Равномерное криволинейное движение. Это движение, при котором модуль скорости остается постоянным, а вектор скорости меняет свое направление.

,

1.6 Равномерное движение материальной точки по окружности

При описании вращательного движения тела величинами S, v и а (путь, скорость, ускорение) пользоваться неудобно, т. к. различные точки (с разными радиусами вращения R) тела за один и тот же промежуток вре­мени совершают разные перемещения и движутся с различными скоростями и ускорениями. Поэтому здесь вводятся специальные, так называемые угловые величины: угол поворота φ, угловая скоростьω, угловое ускоре­ние ε. Для различных точек вращающегося тела они одинаковы.

Р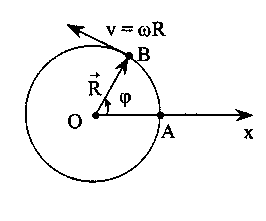 ассмотрим движение материальной точки по окружности радиуса R (рис.). Положение частицы на окружности можно характеризовать уг­лом φ, отсчитывая его от фиксированного радиуса, например, совпадающего по направлению с осью х (ОА на ри­сунке). Тогда аналогом перемещения AS вдоль окружности будет соответствующее этому перемещению изменение угла Δφ. По аналогии со скоростью прямолинейного движения введем угловую скорость точки:

(1.15)

Угловая скорость определяет изменение угла φ (т. е. Δφ) в единицу времени. Измеряя углы в радианах, а время в секундах, в качестве единицы уг­ловой скорости выбирают угловую скорость такого движения, при кото­ром угол φ меняется на один радиан за одну секунду, эту единицу угловой скорости можно обозначить рад/с; обычно ее обозначают просто 1/с или с ^-1.

При равномерном вращении (ω= const) зависимость угла от времени определяется формулой:

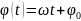(1.16)

Пусть Т - период обращения частицы, т. е. время совершения ею од­ного оборота вокруг центра вращения О. За время Δt = Т угол φ возрастает на 2π, т. е. Δφ = 2π. Поэтому

(1.17)

Введем в рассмотрение число оборотов v в единицу времени - частоту. Так как один оборот совершается за время Т, то, следовательно, за единицу времени будет совершено оборотов

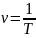(1.18)

Отсюда, учитывая выражение (1.18), получаем еще одно выражение для уг­ловой скорости ω.

(1.19)

Частота v измеряется в оборотах в секунду или герцах Гц. Один герц равен одному обороту в секунду и обозначается Гц =с ^-1.

Нормальное ускорение:

(1.20)

Если вращение неравномерное, угловая скорость является функцией вре­мени. Ее производную по времени называют угловым ускорением.

(1.21)

Угловое ускорение, как видно измеряется в c ^-2.

При равнопеременном вращении ε = const и выражения для ω и φ:

(1.22)

Д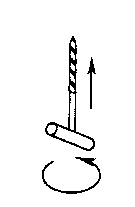 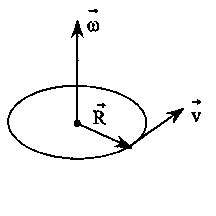о сих пор выражения для угловой скорости и углового ускорения за­писывались в скалярном виде. Теперь рассмотрим эти величины как векто­ры. Для определения направления этих величин необходимо использовать правило буравчика (или правило правой руки): сопоставляем направление вектора угловой скорости с поступательным движением бурав­чика, а вращение линейной скорости - с направлением вращения ручки бу­равчика (рис.).

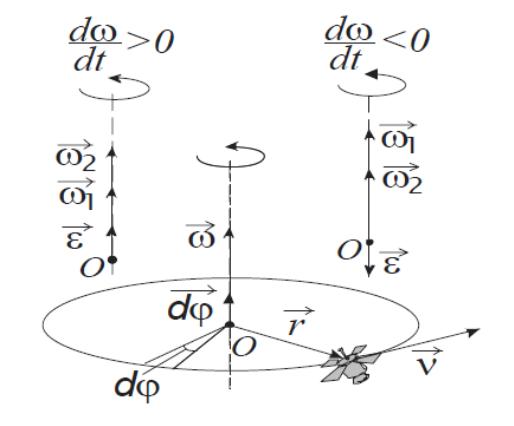
Угловое ускорение определяется . Если движение равноускоренное, то . Если - движение равнозамедленное, то .

Аналогия между поступательными и вращательными величинами:

Поступательное движение	Вращательное движение	Связь величин
Равномерное
Равнопеременное

Глава № 2 ДИНАМИКА

ЛЕКЦИЯ № 2, 3

Тема: Динамика материальной точки и поступательного движения твердого тела.

2.1 Первый закон Ньютона

Кинематика описывает только виды движения тела. Вопросы, связанные с взаимодействием тел, ведущим к измене­нию состояния движения, относят­ся к области динамики.

В основе классической механики лежат законы Ньютона, сформулированные в 1687 г. в знаменитой книге «Математические начала натуральной философии». Три знаменитых закона Ньютона ставшие фундаментом всей классической физики были получены на основе обобщения многочисленных экспериментальных фактов полученных как до Ньютона, так и им самим.

Первый закон Ньютона (этот фундаментальный закон был сформулирован в 1638 г. Галилео Галилеем) может быть сформулирован следующим обра­зом: всякое тело сохраняет состояние покоя или равномерного и пря­молинейного движения, пока воздействие со стороны других тел не за­ставит его изменить это состояние.

Свойство тел сохранять скорость называется инерциейСистема отсчёта относительно, которой выполняется закон инерции, называется инерциальной. Инерциальная система отсчета – это такие системы отсчета, которые двигается относительно друг друга равномерно прямолинейно, либо покоится относительно друг друга. При решении большинства технических задач в качестве инерциальных систем отсчёта используются системы, связанные с Землёй, при этом суточное движение вокруг собственной оси и годовое движение вокруг Солнца не учитывается. Хотя, строго говоря, пренебрежение вращением земли, в ряде задач, таких как ракетные пуски, артиллерийские стрельбы, движение гироскопических устройств, недопустимо.

2.2 Второй закон Ньютона

Из первого закона Ньютона следует, что только воздействие одних материальных тел на другие способно изменить состояние их движения. Это воздействие одних тел на другие характеризуется физической величи­ной, называемой силой F.Изменение состояния движения означает, что тело выходит из состояния покоя или равномерного и прямо­линейного движения, т. е. меняется его скорость, тело приобретает ус­корение. Следовательно, сила характеризует появление у рассматривае­мых тел ускорения в результате воздействий других тел.

Любая сила характеризуется числовым значением, направлением действия и точкой приложения. Прямую, проведенную через точку приложения силы в на­правлении действия этой силы, называют линией действия силы. Сила – векторная величина, так как она имеет направление.

Инертность выражает свойство материальной точки под действием силы изменять свою скорость по модулю и направлению. Величина, определяющая меру инертности точки, называется еёмассой.Инертность тела – это способность тела сохранять состояние покоя или равномерно прямолинейно двигаться.Масса в классической механике является величиной постоянной, скалярной и положительной величиной, отличающей одну материальную точку от другой.

Обычно массу тела определяют взвешиванием на рычажных весах. Этот метод основывается на следующей экспериментально установленной закономерности для свободного падения тел: в одной и той же точке зем­ного шара все тела свободно падают с одинаковым ускорением g. Свобод­ное падение вызывается действием силы тяжести тела . При взвешивании тела на рычажных весах сила тяжести тела и сила тяжести гири (или набора гирь) уравновешиваются, т. ч. масса тела и масса гири (или набора гирь) должны быть равны. Таким образом, зная массы гирь, можно измерить массу тел, взвешивая их на рычажных весах. В сис­теме СИ масса измеряется в килограммах (кг).

Опыт показывает, что одна и та же сила по-разному действует на разные тела. Железнодорожный вагон, например, будет ускоряться мед­леннее, чем маленькая тележка.

(2.1)

Приобретаемое телом ускорение пропорционально силе и обратно пропорционально массе

(2.2)

или

В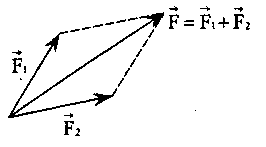 системе СИ единицей силы называется ньютон (Н).

Если на тело одновременно действуют n сил F₁, F₂, ..., F_n, приложенных к одной и той же точке тела, то их можно заменить однойэквивалентной им силой F, равной их векторной сумме и приложенной в той же точке. Силу F называют результирующей или равнодействующей силой.. Силы складываются по правилу сложения векторов.

Понятно, что силы, приложенные к одной и той же точке тела, взаимно уравновешиваются, только если их результи­рующая сила равна нулю.

При воздействии на тело нескольких сил, учитывая, что ускорение и действующие на тело силы являются векторами, можно второй закон Ньютона записать в виде:

(2.3)

Уравнение (2.3) называется еще уравнением движения тела.

Результирующую силу F, действующую на материальную точку, можно разложить на две составляющие - касательную к траектории точки и нормальную к ней F_n:

.. (2.4)

Из уравнения второго закона Ньютона тогда следует что

(2.5)

Нормальная сила F_n так же, как и направлена к центру кривизны тра­ектории. Поэтому ее обычно называют центростремительной силой.

Эта сила вызывает изменение только направления вектора скорости v точ­ки, т. е. искривляет ее траекторию. Численно F_n равна

(2.6)

Изменение численного значения скорости v точки, характеризуемое каса­тельным ускорением а_т, вызывает касательная сила . Если параллельна , то точка движется ускоренно, если противоположна по направлению вектору , то частица движется замедленно. Наконец, при Ft = 0 точка движется равномерно (v = const). Если, кроме того, F_n = const, то точка движется равномерно по траектории с постоянным радиусом кривизны. Из плоских кривых таким свойством обладает только окружность, а из пространственных кривых - винтовая линия.

Вспомнив, что запишем уравнение (2.3) в виде

(2.7)

или , (2.8)

где вектор называется импульсом тела (раньше часто использова­лось название - количество движения). Внести массу под знак производ­ной можно, т. к. масса постоянна. В системе СИ импульс измеряется . Fdt – импульс силы- физическая величина, равная произведению силы на время ее действия.

Уравнение (2.7) - еще одна, часто ис­пользуемая форма записи второго закона Ньютона: скорость изменения импульса материальной точки равна действующей на нее силе.По­этому второй закон Ньютона можно назвать законом изменения импульса.

1) Если на материальную точку действует постоянная сила ( = const), то импульс точки является линейной функцией времени:

, проинтегрируем обе части

(2.9)

2) Если F=0, то импульс точки не изменяется - она движется равномерно и прямолинейно в соответствии с первым законом

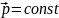
2.3 Третий закон Ньютона

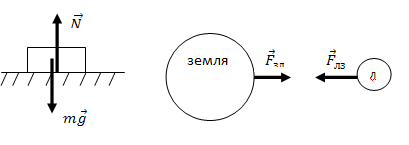
Третий закон Ньютона дополняет содержание второго закон: изменение состояния движения тел происходит в результате их взаимодействия. Если тело 1 действует на тело 2 с силой F₁₂, то тело 2, в свою очередь, действует на тело 1 с силой F₂₁. Третий закон Ньютона утверждает, что силы, с кото­рыми взаимодействующие тела действуют друг на друга, равны по ве­личине и противоположны по направлению.

(2.12)

Существенно то, что силы и («действие» и «противодействие») приложены к разным телам. Это значит, что нельзя подействовать на тело и самому избежать его воздействия (например, стукнуть по стене и не по­чувствовать удара).

Третий закон Ньютона справедлив не всегда. Вполне строго он выполняется при непосредственном соприкосновении тел, а также при взаимодействии находящихся на некотором расстоянии друг от друга покоящихся тел.

2.4 Закон сохранения импульса

Тела, образующие механическую систему, могут взаимодействовать как между собой, так и с телами, не принадлежащими к данной системе. В соответствии с этим силы, действующие на тела системы, можно подразделить на внутренние и внешние. Внутренними называют силы, с кото­рыми на данное тело воздействуют остальные тела системы, внешними - силы, обусловленные воздействием тел, не принадлежащих системе. В случае, когда внешние силы отсутствуют, система называется замкнутой.

Рассмотрим систему, состоящую из n точечных частиц. В частности, 1 в виде так:₀й системы можно представить и твердое тело Присвоим частицам номера от 1 до n и обозначим силу, действующую со стороны i-й частицы на j-ю через F_ij. Кроме того, на частицы могут действовать внешние силы. Обозначим результирующую силу, действующую со стороны внешних тел на i-ю частицу, через Ф_i.

Напишем уравнение движения для каждой из частиц системы:

………………………………..

(2.13)

Сложим почленно все n выписанных уравнений (2.13). Заметим, что в сумму справа войдет, например, такая пара: F₂₁ из первого уравнения и F₁₂ - из второго, Но согласно третьему закону Ньютона:

.

Поэтому все внутренние силы уничтожаются при суммирова­нии. С другой стороны, после такого суммирования слева будет стоять производная от суммы импульсов всех частиц, т. е. от полного импульса системы

В итоге получаем

(2.14)

Напомним, что Ф_i - это результирующая внешняя сила, действующая на i-ю частицу системы.

Или

В незамкнутой системе изменение импульса системы равно импульсу внешней силы.

Импульс системы материальных тел не может быть изменен внутренними силами, а может быть изменен только внешними силами.

Предположим, что векторная сумма внешних сил равна нулю , т.е. система частиц замкнута. В этом случае 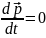и, следовательно, , т. е. в замкнутой системе полный импульс системы частиц сохраняется. Это утверждение называют законом сохранения импульса.

2.5 Цент масс

Импульс системы может быть выражен через скорость ее центра масс. Центром масс (или центром инерции) системы материальных точек называет­ся воображаемая точка С, положение которой характеризует распределение массы этой системы.

Найдем ее координаты. Запишем уравнение для изменения импульса материальных точек:

(2.15)

Здесь мы вначале учли определение импульса одной частицы, затем домножили и разделили выражение на полную массу всей системы (при этом величина дроби не изменилась), ввели некоторый вектор Полученное выражение показывает, что полный импульс системы частиц может быть представлен как .

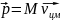Преобразуем выражение (2.15) дальше:

(2.16)

Выражение (2.16) - уравнение движения центра масс. Масса сосредоточена в точке с радиусом-вектором

Эта точка и называется центром масс или центром инерции системы частиц. В проекции на ось Х, например,

(2.17)

Итак: если всю массу системы частиц (или в частном случае твердого тела) сосредоточить в ее центре масс, то импульс этой воображаемой частицы будет равен полному импульсу системы.

Скорость центра масс равна отношению импульса замкнутой системы к массе этой системы

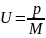
Задача 1

Механическая система состоит из трех частиц m₁ = 0,2 г , m₂ = 0,3 г, m₃ = 0,4 г. Первая частица находится в точке с координатами (1; 2; 3), вторая с координатами (1; 1;0), третья – в точке (3; 2; 1). Найти Х – координату центра масс.

Задача 2

В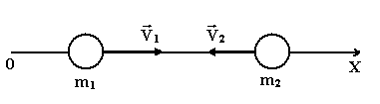 доль оси OX навстречу друг другу движутся две частицы с массами m₁ = 2 г и m₂ = 3 г и скоростями V₁ = 2 м/с и  V₂ = 3 м/с соответственно. Проекция скорости центра масс на ось ОХ (в единицах СИ) равна …

/с двигается против оси х

2.6 Закон всемирного тяготения, сила тяжести, вес

В 1678 г. Ньютон установил, что любое падение тел вызывается при­чиной общего характера, что между любыми земными телами, телами Солнечной системы, между любыми частицами, существующими во Все­ленной, возникают силы тяготения (гравитационные силы). Закон, которо­му подчиняются силы тяготения, гласит: любые два тела притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними. Уста­новленный Ньютоном закон получил название закона всемирного тяготе­ния. Математически он записывается так:

где m и М - массы взаимодействующих тел; г - расстояние между телами; G- гравитационная постоянная, равная 6,67 • 10 Н∙м²/кг².

Рассмотрим взаимодействие тела с Землей. Пусть М - масса Земли. Поместим начало координат в центр Земли. Тогда в векторной форме оп­ределение можно записать в следующем виде:

Из этого закона, в частности, следует, что у поверхности Земли все тела должны падать с одинаковым ускорением. Речь идет о свободном па­дении тел при отсутствии сил сопротивления (также не принимается во внимание зависимость силы тяжести от широты местности). Действитель­но, ускорение, приобретаемое телом массой m:

g - ускорение свободного падения, R₃ - радиус Земли. Но т. к. R₃ и М являются величинами постоянны­ми (Земля считается шаром), то получаем, что все тела у поверхности Зем­ли, независимо от их массы, падают с одинаковым ус­корением g. Выражение имеет важное значение еще и потому, что позволяет вычислить ускорение силы тяжести на любом небесном теле.

СИЛА ТЯЖЕСТИ ВЕС………..

Из опыта известно, что всякое тело, движущееся горизонтально, при отсутствии действия на него других сил с течением времени замедляет свое движение и в конце концов останавливается. Это объясняется существованием силы трения, которая препятствует скольжению соприкасающихся тел. Силы трения зависят от относительных скоростей тел, в результате их действия механическая энергия всегда превращается во внут­реннюю энергию соприкасающихся тел, т. е. в энергию теплового движения ча­стиц.

Различают внешнее (сухое) и внут­реннее (жидкое или вязкое) трение. Внешним трением называется трение, возникающее в плоскости каса­ния двух соприкасающихся тел при их относительном перемещении. Если со­прикасающиеся тела неподвижны отно­сительно друг друга говорят о трении покоя, если же происходит относитель­ное перемещение этих тел, то в зависи­мости от характера их относительного движения говорят о трении скольже­ния, качения или верчения.

Внутренним трением называется трение между частями одного и того же тела, например между различными слоями жидкости или газа, скорости которых меняются от слоя к слою.

При скольжении относительно друг друга двух твердых тел, разделенных прослойкой вязкой жидкости (смазки), трение происходит в слое смазки. В таком случае говорят о гидродинамическом трении (слой смазки достаточно толстый) и граничном трении (толщина смазочной прослойки составляет около 0,1 мкм и менее). I

трение

Гидродинамическое или

Граничное

трение

Внешнее трение

Внутреннее трение

Трение покоя

Трение скольжения

Трение качения

Трение верчения

Р ассмотрим внешнее трение. Это трение обус­ловлено шероховатостью соприкасаю­щихся поверхностей, а в случае очень гладких поверхностей — силами меж­молекулярного притяжения.

1) Пусть на горизонтальном столе лежит тело мас­сой m. Пусть на это тело начинает действовать горизонтально направленная сила (рис.). Если сила достаточно мала, тело не сдвинется с места.

Только если величина силы превысит некоторое значение , начнется скольжение. При этом ускорение тела будет меньше, чем это следует из второго закона Ньютона, если считать, что вдоль поверхности соприкосновения действует лишь сила F . Причина понятна: вдоль поверхности на тело со сто­роны стола действует сила трения, препятствующая движению.

Сила трения обусловлена взаимодействием молекул, находящихся в тонких слоях на поверхностях тел иявляются по своей природе электромагнитными силами. Законы, описывающие сухое трение, установил опытным путем Шарль Кулон в 1781 г. Согласно Кулону величина силы трения скольже­ния пропорциональна силе нормального давления:

(2.13)

Здесь введен безразмерный коэффициент трения μ,зависящий от мате­риалов, из которых сделаны взаимодействующие тела, и от состояния по­верхностей (качества шлифовки, степени загрязнения).

При проскальзывании сила трения направлена против скорости.

Характерным свойством сухого трения является то, что сила может быть отлична от нуля и при отсутствии проскальзывания. Вернемся к при­меру на рис.. При внешней силе тело, лежащее на столе, не дви­жется. Ясно, что в этом случае сила трения равна по величине и противо­положна по направлению внешней силе:

Когда отсутствует проскальзывание, силу трения называют силой трения покоя. Оказывается, что с хорошей точностью максимальное значение си­лы трения покоя F₀ равно силе трения скольжения. Иными словами, сила сухого трения меньше или равна произведению коэффициента трения на силу нормального давления.

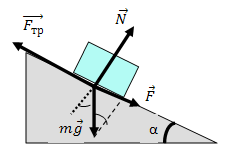
2) Если тело находится на наклонной плоскости с углом наклона α (рис.), то

При малых углах α сила и тело лежит неподвижно на наклонной плоскости. По мере увеличения угла α сила F возрастает и при некотором угле α_0, называемом углом трения, становится равной . При тело скользит по наклонной плоскости. Рассмотрим предельный случай:

Т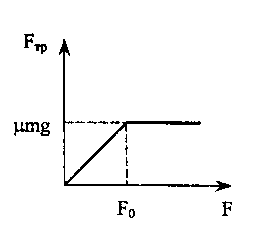 аким образом, коэффициент трения равен тангенсу угла а₀, при кото­ром начинается скольжение тела по на­клонной плоскости.

График зависимости силы трения от внешней силы F приведен на рис. Проскальзывание начнется при некотором значении внешней силы F₀, ко­гда сила трения покоя достигнет своего максимального значения.

При движении тел в жидкостях или газах также возникает сила, пре­пятствующая движению. Ее происхождение связано как с возникновением в среде разности давлений, так и с «трением» слоев среды, вовлеченных телом в движение, - вязкостью.

В отличие от сухого трения в этом случае не возникает трения покоя -при нулевой скорости жидкое трение равно нулю. Поэтому даже очень маленькая внешняя сила может сообщить относительную скорость слоям вязкой жидкости.

С илы трения играют большую роль в природе. В нашей повседневной жизни трение нередко оказывается полезным. Вспомним трудности, воз­никающие во время гололедицы, когда трение между покрытием дорог и подошвами пешеходов или колесами транспорта сильно уменьшается. Во многих случаях роль трения оказывается отрицательной и приходится ка­ким-либо образом его уменьшать. Наиболее радикальным способом уменьшения сил трения является замена трения скольжения трением каче­ния, возникающим, например, между цилиндрическим или шарообразным телом и поверхностью, по которой оно катится. Для этой же цели исполь­зуются различные виды подшипников и смазки. Кроме трения качения есть сила трения верчения. Различие этих движений состоит в следующем.

П ри качении (например, цилиндра по плоскости) точки контакта соприкасаются лишь на мгновение, и одно из тел вращается вокруг мгновенной оси, проходящей через точки контакта. При верчении (например, оси волчка на опоре, стрелки компаса вокруг острия — ее опоры) точки контакта соприкасаются длительно. В случае верчения трение связано со скольжением в местах контакта. Для его умень­шения применяют острия с малыми радиусами закругления и увели­чивают твердость острия и опорной поверхности.

Для силы трения качения справедлив закон: (2.14)

Сила трения качения обратно пропорциональна радиусу катящегося тела.

Глава № 3 РАБОТА И МЕХАНИЧЕСКАЯ ЭНЕРГИЯ

ЛЕКЦИЯ № 4, 5