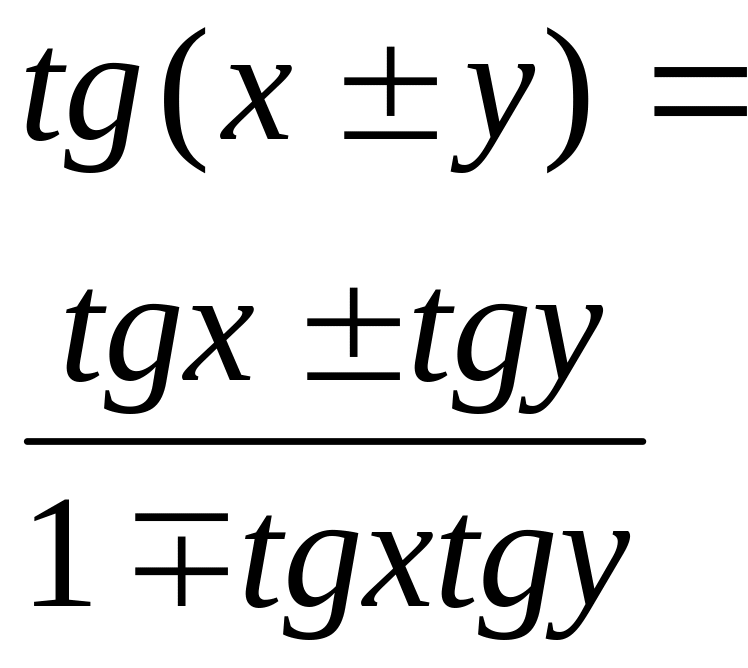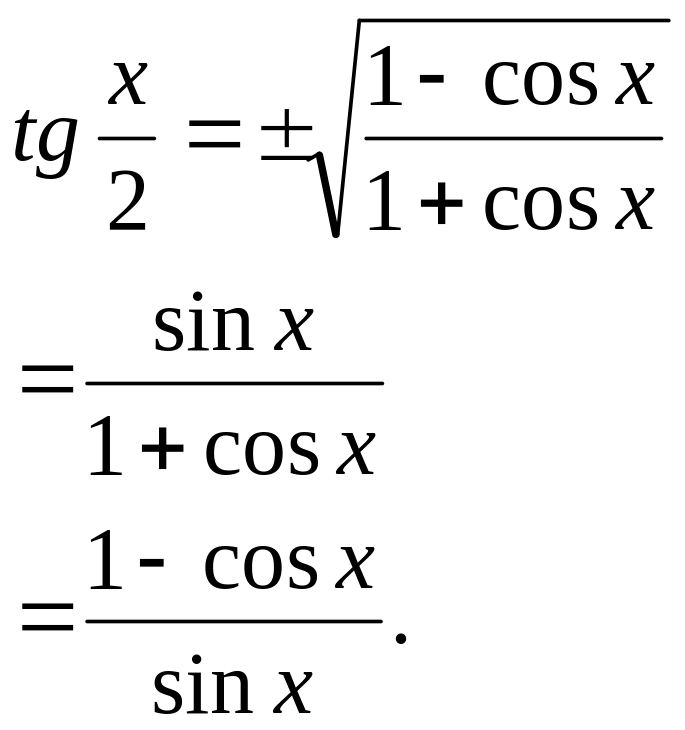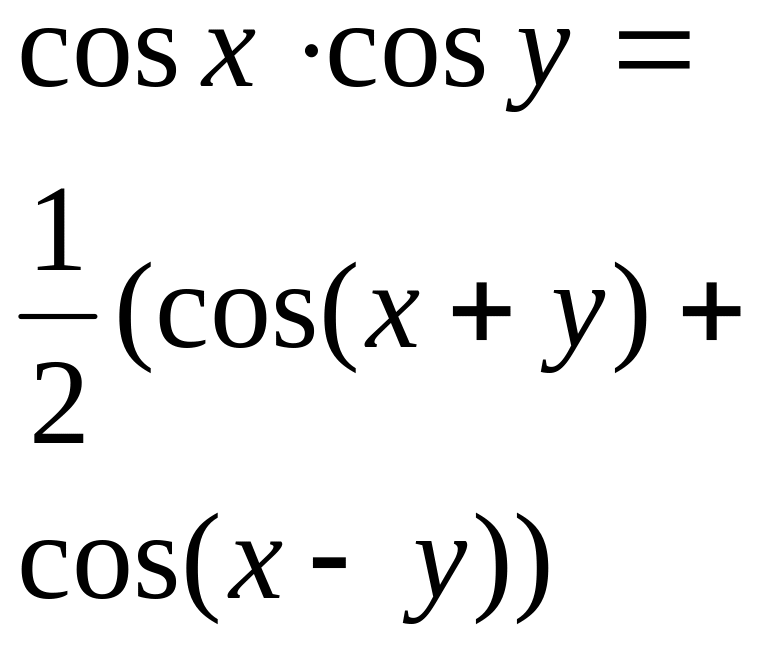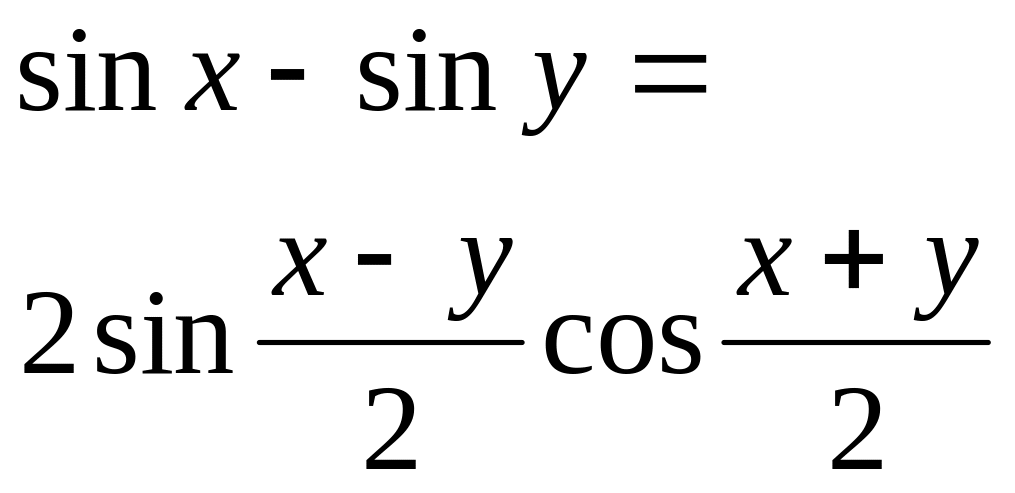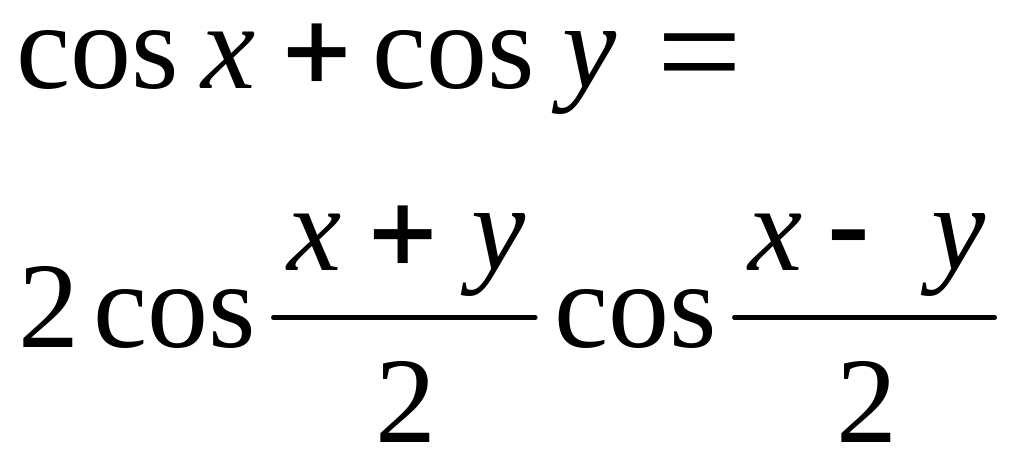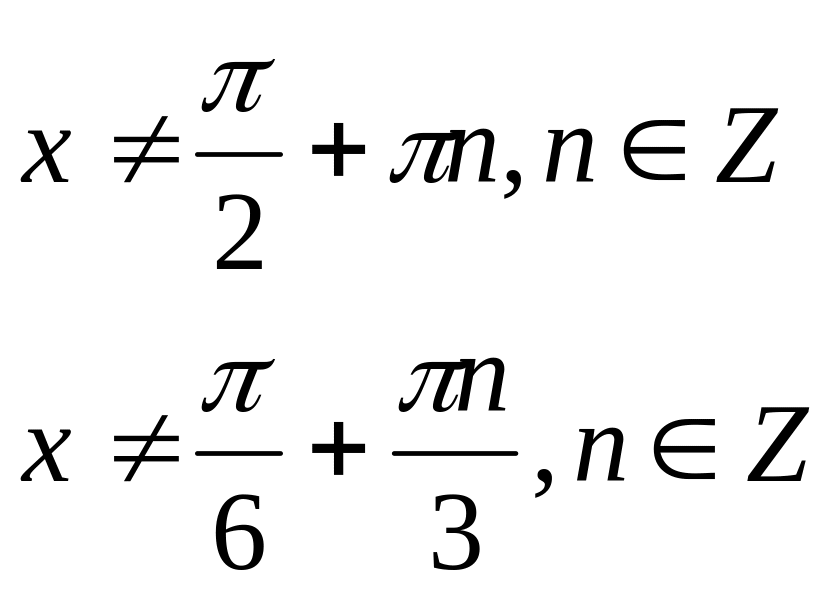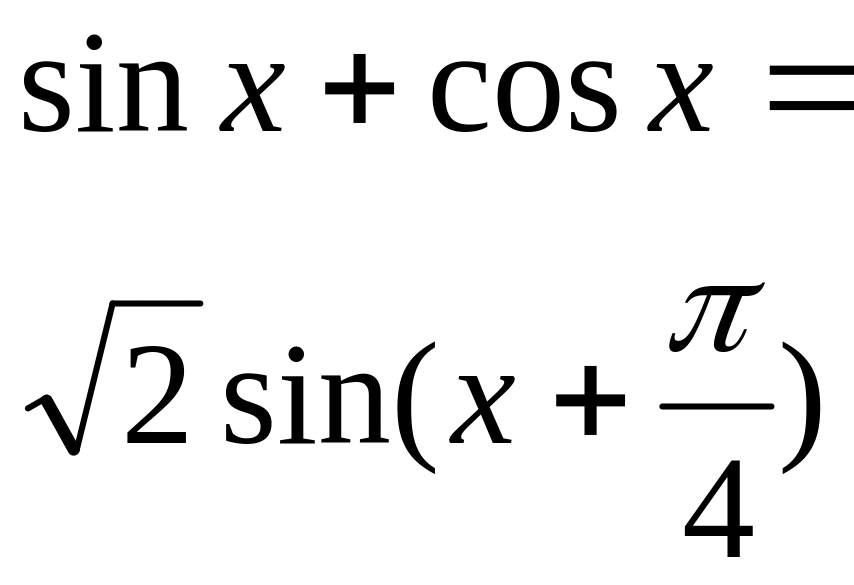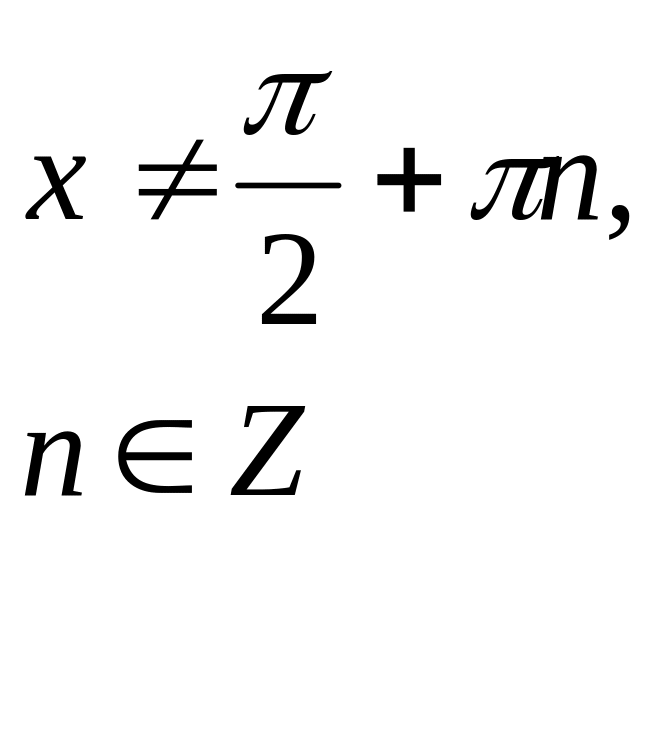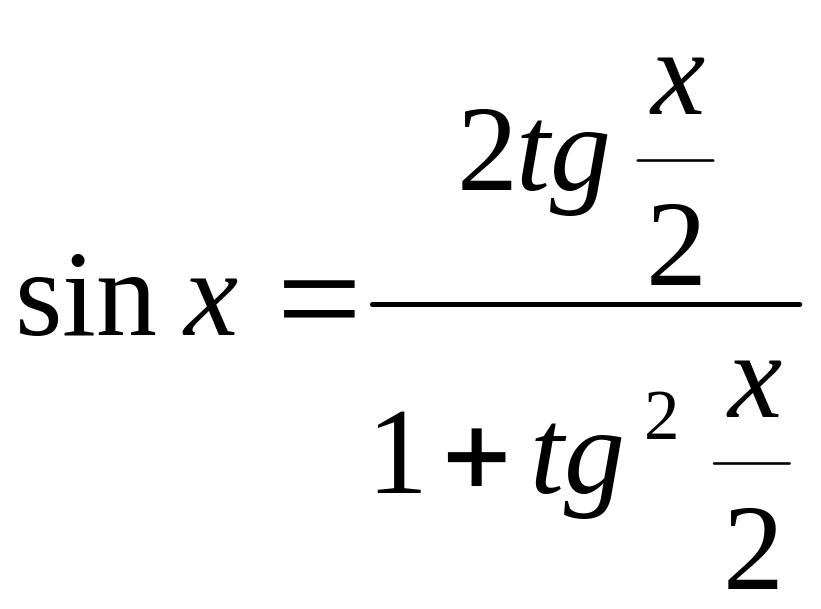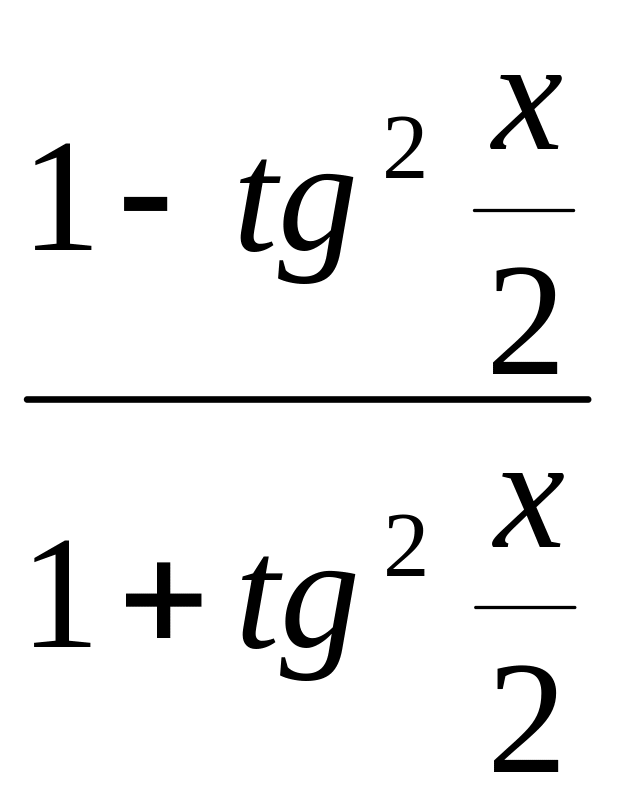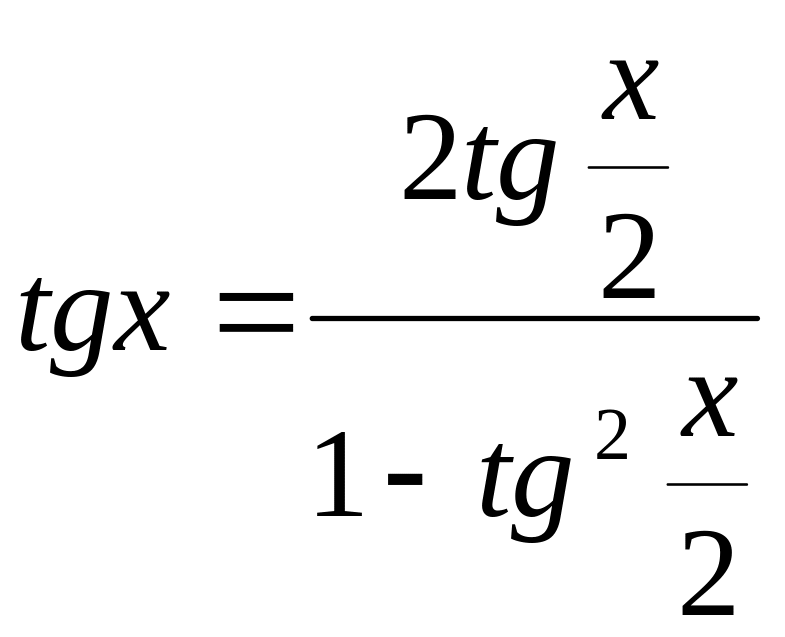Наиболее часто встречающиеся ошибки

Название формулы

Формула

Применение в преобразованиях

Применение для исследования свойств функций

Примечания

Основная тригонометрическая единица

sin²x + cos²x =1

Выражение синуса через косинус и наоборот

Формула справедлива для любых значений аргумента

Зависимости между тригонометрическими функциями одного и того же аргумента

Выражение одних тригонометрических функций через другие тригонометрические функции того же аргумента

Для оценки множества значений функции применяется неравенство

tgx ·ctgx =1

Формулы сложения

Выражение тригонометрических функций суммы аргументов через

тригонометрические функции слагаемых.

Выражение тригонометрических функций разности аргументов через

тригонометрические функции уменьшаемого и вычитаемого

Представление суммы произведений тригонометрических функций в виде одной функции для оценки множества значений функции.

Формулы синусов и косинуса справедлива для любых значений аргумента

Формулы для тангенсов справедливы для следующих значений аргумента

x±y≠ π/2+ πn, x≠π/2+πk, y≠π /2+πm, n,m,k –целые числа.

Синус суммы двух углов

sin(x +y)

= sinxcosy +

sinycosx

Синус разности двух углов

sin(x-y) =sinxcosy - sinycosx

Косинус суммы двух углов

cos(x+y)= cosxcosy- sinxsiny

Косинус разности двух углов

cos(x-y)= cosxcosy- sinxsiny

Тангенс суммы

(разности) аргументов

Тригонометричские функции двойного аргумента

sin2x = 2sinxcosx

cos2x =

cos² x - sin² x

tg2x =

Формулы позволяют от данного аргумента перейти к аргументу, в два раза меньшему, например,

sin10x = 2sin5x·cos5x

Для оценки множества значений функций; для

представления данного выражения в виде однородного относительно тригонометриических функций

Синус двойного аргумента:

Косинус двойного аргумента:

Тангенс двойного аргумента:

Синус половинного аргумента:

Косинус половинного аргумента:

Тангенс половинного аргумента:

Формулы позволяют от данного аргумента перейти к аргументу, в два раза большему , например,

( sin5x = ± ),

для понижения

степени выражения.

Для оценки множества значений функций;

для определения четности или нечетности, периодичности функции

Произведение тригонометрических функций

Для приведения подобных слагаемых при разложении нескольких произведений в сумму

Для определения периода функций

Произведение синуса и косинуса числа

Произведение синусов

Произведение косинусов

Сумма и разность тригонометрических функций

Для, прямого разложения выражения на множители,

для разложения на множители способом группировки слагаемых

Для определения нулей функции, знаков функции, промежутков монотонности

Формулы справедливы для любых значений переменных

Сумма синусов

Разность синусов

Сумма косинусов

Разность косинусов

Линейное выражение относительно sinx и cosx

При решении тригонометрических уравнений

Для оценки множества значений функций; определения наибольшего и наименьшего значения функции

Формулы справедливы для любых значений переменных

Формулы приведения

Если в формуле приведения, аргумент α

прибавляется к числу π/2(или вычитается из числа π/2), взятого нечетное

число раз, то название функции меняется на

«кофункцию»:

б) если в формуле приведения аргумент α прибавляется к числу π/2(или вычитается из числа π/2), взятого четное

число раз, то название функции не меняется;

в) знак приведенной функции определяется по знаку приводимой функции в соответствующей четверти, считая угол α острым.

При переходе от тригонометрических функций суммы или разности к тригонометрической функции одного аргумента.

При замене одной тригонометрической функции на «кофункцию».

Для определения знаков функции, вычисления значений функции, построения графиков с помощью преобразований

Формулы справедливы для любых значений переменных из области определения функций

Формулы тройного аргумента

Для перехода от данного аргумента к аргументу в три раза меньшему.

Для понижения степени выражения.

Для оценки множества значений функции, периода функции, знака, промежутков монотонности

Синус тройного аргумента

Косинус тройного аргумента

Тангенс тройного аргумента

Сумма синуса и косинуса числа

Для решения уравнений вида

sinx +cosx= a

Для оценки множества значений функции, знака функции и пр.

Формула справедливы для любых значений переменных

Выражение тригонометрических функций через тангенс половинного угла

Для перехода к однородному выражению при решении тригонометрических уравнений

Для оценки множества значений функции, знака функции и пр.

Выражение синуса числа через тангенс половинного аргумента

Косинус через тангенс половинного аргумента

cosx=

Тангенс числа

через тангенс половинного аргумента

1

Вычислите , если

1)2; 2)-1; 3) 1; 4) 0;5)0,5.

2

2

Вычислите sin 4 x, если tg (x - 45°) = -2

1)24/25; 2)-4/5;

3) – 24/25; 4)4/5; )- 0,5.

3

3

Вычислите sin(x+ 60°), если известно, что и угол α находится в третьей четверти.

1) ; 2) ;

3) ;4) ;5) .

1

4

Вычислите tg(x- 45°), если cos x = - 9/41 и угол x находится в третьей четверти.

1)-31/49; 2)-4/7; 3) – 24/49; 4)4/5;5) 31/49.

5

5

Известно, что . Найдите значение выражения

1)-10; 2)4; 3) 8; 4) 10; 5)5.

4

6

Найдите значение tgx + tgy + tgz,

если x + y + z = π, tgx ·tgy · tgz = 4

1)1; 2)4; 3) 6; 4) - 4; 5) 3.

2

7

Результат упрощения выражения равен

1) 2 cos2x; 2) - cos2x; 3) 2; 4) 2 sin 2x; 5)- 2 sin2x.

1

8

Найдите наибольшее и наименьшее значение функции

на отрезке [0; π/2]

1) 2; 0; 2)1;-1; 3) 1; 0;4) 2; 0,5; 5) 2;-2.

3

9

Значение выражения равно

1) ; 2) ; 3) - ; 4) - 4; 5) 3.

3

10

Если ctg 2α =-3, то значение выражения равно

1)1; 2)-2/3; 3) 6; 4) 2/3; 5)-6.

4

11

Найдите ctg α

1) 2; 2)4; 3) 6; 4) - 4;

5) -2.

5

12

Результат упрощения выражения

равен:

1)1; 2)cos² x; 3) sin² x; 4) 2; 5) -2.

1

13

Значение выражения

cos 95° cos 5° + 0, 5( sin 10°+1) равно

1)1; 2)-1,5; 3) 0,5; 4) 1,5; 5)-0,5 .

3

14

Вычислите значение выражения:

1) 0,5; 2)1; 3) 6; 4) - 1; 5) -2.

4

15

Найдите tgx, если

1) 0, 5; 2)1; 3) 6; 4) - 1; 5) 2.

5

16

Результат упрощения выражения

равен

1) ; 2) ; 3) ; 4) - 1; 5) .

1

17

Вычислить , если

1)-125/78; 2)1/2; 3)125/78; 4) – 1/2;

5) 2/27.

3

18

Значение выражения:

равно:

1) -0, 5; 2)1; 3)0,5;

4) - 1; 5) -2.

3

19

Значение выражения

равно:

1) 0,25; 2)-0,125; 3)0,125; 4) – 0,25; 5) -2.

2

20

Значение выражения

равно:

1) - 0, 25; 2)1; 3)0,125;

4) 0,25; 5) -2.

1

21

Результат упрощения выражения

6cos² α tgα - 8 sin2α

равен

1) 2 cos2x; 2) - cos2x;

3) 2; 4) 2 sin 2x;

5)- 5sin2x.

5

22

Значение выражения cos 80°sin50° sin110°

равно

1) 0,25;

2)-0,125; 3)0,125;

4) – 0,25; 5) -2

3

23

Если , то

равно

1) ; 2) ; 3)mn;

4)m+n; 5)m-n.

1

24

Результат упрощения выражения равен

1) 2 cos2α; 2) - cos2 α;

3) 2; 4) sin 2 α;

5)- 5sin 2α.

4

25

Результат упрощения выражения

равен

1) -0, 5; 2)1; 3)0,5;

4) - 1; 5) -2.

4