3. Формулы приведения

Формулы приведения позволяют от тригонометрических функций аргумента +α, перейти к тригонометрическим функциям аргумента α.

Н апример, sin(π/2+α) = cos α, cos(π+α) = - cos α.

Правило:

а) если в формуле приведения (например, cos(5π/2+α) ) аргумент α

прибавляется к числу π/2(или вычитается из числа π/2), взятого нечетное

число раз( в нашем случае 5раз ), то название функции меняется на

«кофункцию»: синус- на косинус, косинус- на синус, тангенс- на котангенс (в нашем случае название функции косинус изменится на синус);

б) если в формуле приведения (например, cos(3π +α) ) аргумент α прибавляется к числу π/2(или вычитается из числа π/2), взятого четное

число раз( в нашем случае – 6 раз, 3π =6· π/2 ), то название функции не меняется;

в) знак приведенной функции определяется по знаку приводимой функции в соответствующей четверти, считая угол α острым ( так как 5π/2+α принадлежит второй четверти, а во второй четверти косинус принимает отрицательные значения, то cos(5π/2+α)=-sinα; угол 3π +α принадлежит третьей четверти, а в третьей четверти косинус принимает отрицательные значения, значит, cos(3π +α)=-cos α).

Примеры

а) Найдите: сos 210°; sin(-135°); tg (11π/6).

Решение.

сos 210°= cos(180˚+30˚) =-cos30˚=- /2, так как 180˚=90˚·2(π/2 взято четное число раз), то название функции не меняется; угол 180˚+30˚ находится в третьей четверти , значения косинуса в ней отрицательны, поэтому перед приведенной функцией поставлен знак «- ».

sin(-135°) =-sin(90° +45°)=- cos45° = - /2

tg (11π/6) = tg (2π- π/6)=-tg π/6=- /3

б) Упростите выражение:

Решение.

= = =

= =

4.A) Формулы двойного аргумента

1. Синус двойного аргумента: sin2x = 2sinxcosx

2. Косинус двойного аргумента: cos2x = cos² x - sin² x

3. Тангенс двойного аргумента:

tg2x =

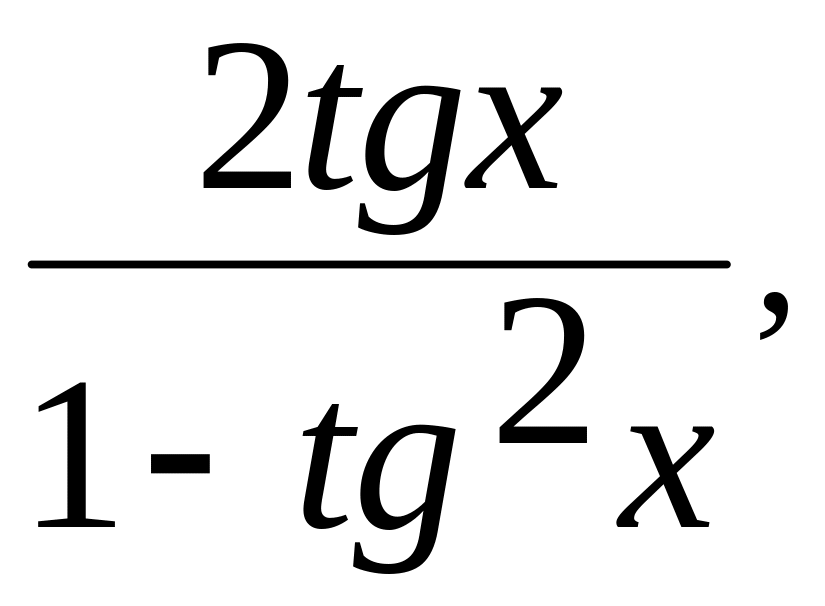
Пример

Найдите sin2α; cos2α; tg2α, если tgα=5, α [0; π/2]

Решение.

Запишем формулу синуса двойного аргумента: sin2α = 2sinαcosα.

В правой части этой формулы не известны sinα и соsα.

Из формулы tg² α +1 = 1/ cos² α найдем cos α .

соs α = . Из формулы sin² α +соs²α=1 найдем

sinα. sinα = . Подставим найденные значения sinα и соs α в формулу синуса двойного аргумента: sin2α = 2sinαcosα =

=

cos2α найдем из формулы косинуса двойного аргумента:

соs 2α = cos²α – sin²α = .

tg2α =

б) Формулы половинного аргумента

1.Синус половинного аргумента: six

2.Косинус половинного аргумента: cos

3.Тангенс половинного аргумента:tg X

Пример

Решение.

Найдите sinx, cosx, tgx, если cos2x= , x [π/2; π].

По формуле синуса половинного аргумента найдем sinx= = Выбираем знак «+», так как x [π/2; π](вторая четверть), sinx в этой четверти положительный.

По формуле косинуса половинного аргумента найдем соsx= = 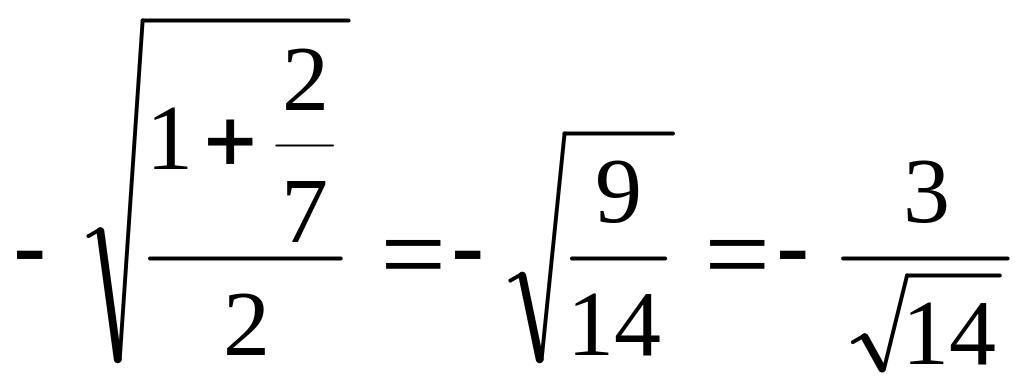, выбираем знак «-», так как x [π/2; π](вторая четверть), cosx в этой четверти отрицательный.

tgx =

5. Формулы cуммы и разности одноименных

тригонометрическихфункций (синуса и косинуса).

1.Сумма синусов двух углов:

sinx +siny =2sin cos

2. Разность синусов двух углов:

sinx - siny =2sin cos

3. Сумма косинусов двух углов:

cosx +cosy =2cos cos

4. Разность косинусов двух углов:

cosx – cosy = -2 sin sin

Пример

Упростите:

Решение.

К числителю дроби применим формулу разности синусов, а к знаменателю –формулу суммы косинусов, получим:

=

По формуле синуса двойного аргумента заменим: =2 , а

соs , получим = .
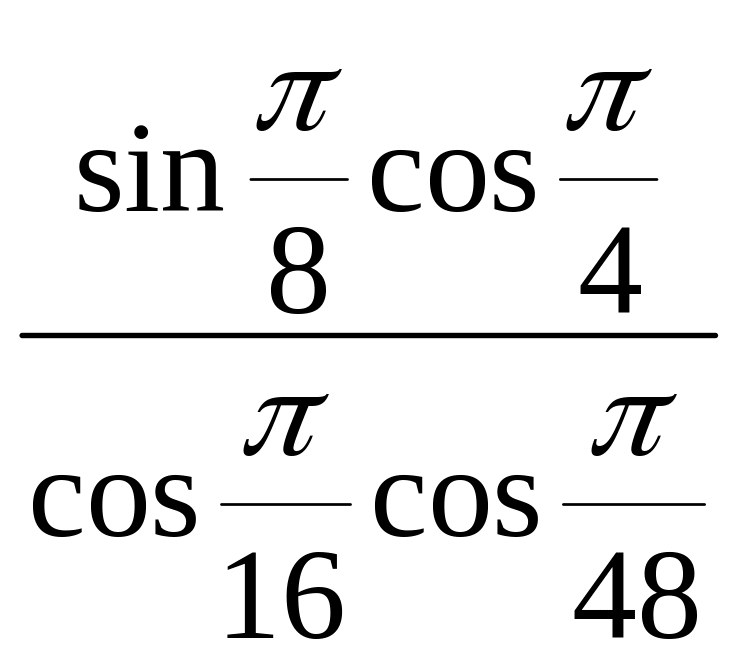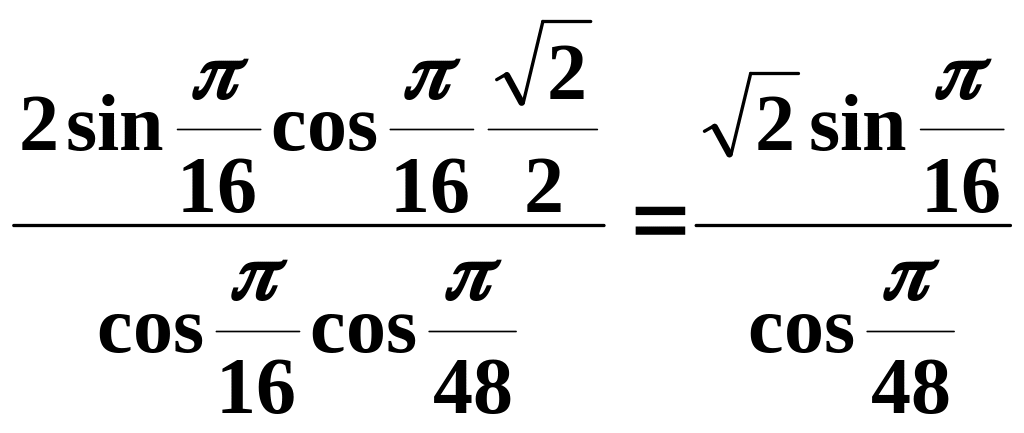